Курсовая работа ИЗУЧЕНИЕ ИНТЕРФЕРЕНЦИИ СОВЕРШЕННОЙ СКВАЖИНЫ ПРИ ФИЛЬТРАЦИИ НЕФТИ И ГАЗА. Платонов В.И. Курсовая работа. Изучение интерференции совершенной скважины при фильтрации нефти и газа
 Скачать 1.67 Mb. Скачать 1.67 Mb.
|
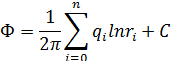 где n—число всех скважин. Последовательное расположение точки М на контуре каждой скважины позволило составить систему (11)—(14), (n+1) 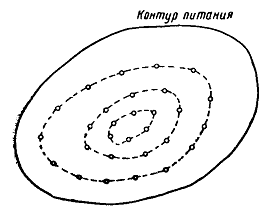 Рисунок 7 – Контур питания кольцевой батареи скважин [13] Уравнений для n дебитов qi = 1, 2, . . ., n и постоянной (15) Такие уравнения выписываются теперь для какой-либо одной «опорной» скважины каждого ряда. При этом предполагается, что в каждом ряду скважины находятся в одинаковых условиях, т. е. имеют одинаковые забойные давления и одинаковые радиусы. [14] Допущение о равнодебитности скважин, как показывают подсчеты, практически мало отражается на величине суммарного дебита скважин. Дебит какой-нибудь одной скважины будет отличаться от расчетного, но если подсчитывать суммарный дебит батареи или всего месторождения, то он будет довольно близким к действительности. [5] Расстояния rij между центрами i-й и j-й скважин могут быть взяты прямо из плана расположения скважин на месторождении. [5] Задача же решения системы уравнений с малым числом неизвестных не вызывает никаких затруднений. Для контроля можно повторить расчет, выбрав другие «опорные» скважины в каждом ряду. Если точность окажется недостаточной, следует обратиться к более точным методам или к электромоделированию. ИНТЕРФЕРЕНЦИЯ СКВАЖИН ВУСЛОВИЯХ УПРУГОГО РЕЖИМА Дифференциальное уравнение упругого режима является линейным, то к его решению приложим метод суперпозиций, рассмотренный выше, который позволит исследовать интерференцию скважин в условиях упругого режима. При помощи метода суперпозиции можно исследовать перераспределение пластового давления, вызванное пуском, остановкой или изменением темпов отбора жидкости из скважин. [15] Рассмотрим несколько примеров использования метода суперпозиции при интерференции скважин в условиях упругого режима фильтрации. Поиск возможного снижения давления в любой точке пласта. Пусть в бесконечном пласте одновременно работают n скважин с постоянными дебитами. Начальное пластовое давление в невозмущенном пласте всюду одинаково и равно рk . Требуется найти снижение давления На основе метода суперпозиции снижение пластового давления в точке М будет равно алгебраической сумме снижений давления в этой точке, вызванных независимой работой каждой скважины, т.е. интерференция скважина фильтрация нефть [2]  Снижение давления в точке М при работе одной n -й скважины по формуле определения давления составит: [2]  Следовательно, при работе всех я скважин снижение давления в точке М определяется из равенства:  (26) (26)где Qi - дебит i-й скважины (при этом дебит добывающей скважины считается положительным, дебит нагнетательной - отрицательным); расстояние от центра i-й скважины до точки М, где определяется: понижение пластового давления; ti - время с начала работы i-й скважины до момента времени t, в который определяется понижение давления. [2] Определение давления в любой точке пласта как при работе скважины, так и после ее остановки. Пусть в некоторый момент времени, принимаемый за начальный (г= 0), в невозмущенном пласте с давлением рk пущена в эксплуатацию скважина с постоянным дебитом Q и через промежуток времени t1 остановлена. Под остановкой ее подразумевается мгновенное прекращение притока жидкости к забою скважины. Требуется определить давление в любой точке пласта в любой момент времени как при работе скважины, так и после ее остановки. До момента времени t1 скважина работала одна, следовательно, пластовое давление в любой точке пласта определяется по формуле:  (27) (27)где t изменяется в интервале от 0 до t1. [2] Начиная с момента времени t1 (скважина уже остановлена), следуя методу суперпозиции, мысленно допустим, что вместе с продолжающей работать добывающей скважиной в той же точке начала работать нагнетательная скважина с таким же расходом Q. Следовательно, с момента t1 в пласт в одной и той же точке закачивается столько же жидкости, сколько из него и отбирается, значит суммарный фактический отбор жидкости из пласта оказывается равным нулю, что свидетельствует об остановке добывающей скважины по условию задачи. [1, 2] К моменту времени t после остановки скважины (t > t1 ) понижение давления в любой точке пласта определяется по методу суперпозиции:  График изменения забойного давления при работе и остановке добывающей скважины приведен на (рисунок 8). 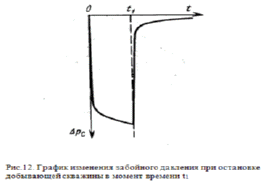 Рисунок 8 – График изменения забойного давления при работе и остановке добывающей скважины приведен [15] Следует отметить, что подъем давления на забое возмущающей скважины начинается сразу же после ее остановки, с момента t1 . В любой другой точке пласта после момента времени t1 будет еще некоторое время продолжаться снижение пластового давления, причем, чем дальше находится эта точка пласта от возмущающей скважины, тем дольше в ней будет продолжаться процесс понижения давления после остановки скважины. Затем и в этой точке пласта начинается повышение давления. [2] Изучение процесса перераспределения давления в полубесконечном закрытом пласте после пуска скважины. Допустим, что однородный пласт имеет бесконечную прямолинейную непроницаемую границу АОВ (рисунок 9).  Рисунок 9 – Схема полубесконечного пласта ч прямолинейной непроницаемой границей. [15] В этом пласте в момент времени t = 0 пущена в эксплуатацию с постоянным дебитом Q одна скважина, например скв. 1. [2] Требуется изучить процесс перераспределения давления в таком пласте после пуска скважины. Используя метод отображения источников и стоков , зеркально отобразим скв. 1 относительно непроницаемой границы АОВ, и дебиту отображенной скважины (скв. 2) припишем тот же знак, что и у реальной скв. 1, т.е. будем считать скв. 2 добывающей с дебитом Q. [2] Условия работы скв. 1 в полубесконечном пласте будут точно такими же, как при работе двух скважин- скв. 1 и скв. 2 - в бесконечном пласте. [2] Используя метод суперпозиции, понижение пластового давления в точке М найдем как сумму понижений давления, вызванных работой указанных скважин в воображаемом бесконечном пласте, т.е.  При наличии в полубесконечном пласте нескольких скважин, каждую из них следует зеркально отобразить относительно прямолинейной непроницаемой границы. Применение метода отображения источников и стоков совместно с методом суперпозиции позволяет выяснить влияние прямолинейного контура питания на процесс перераспределения пластового давления. В этом случае все реальные скважины отображаются симметрично относительно этого контура, и дебитам отображенных, скважин приписываются противоположные знаки по отношению к дебитам реальных скважин (т. е. добывающие скважины отображаются нагнетательными, и наоборот). Методом суперпозиции реальных и отображенных скважин исследуется процесс изменения пластового давления в любой точке. [15, 2] ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ИССЛЕДОВАНИЙ ИНТЕРФЕРЕНЦИИ СКВАЖИН Исследований интерференции скважин может помочь в решение различных задач связанных с работой нескольких скважин. При этом полученные знания можно применять как для решения простейших задач, так и для более трудных, связанных, например, c изменением эффекта взаимодействия в зависимости от числа скважин. Для более наглядной картины рассмотри примеры решения таких задач, начнём с простейшей задачи об условиях заглушения одной из двух скважин в процессе их взаимодействия. Так с помощью формул   легко решить вопрос о заглушении новой скважины А2 ранее пущенной скважины А1, если в ней поддерживается постоянное динамическое забойное давление р1. Положим в упомянутых формулах  (28) (28)Считая, что в обеих скважинах удельные веса жидкости одинаковы, заменим отношения перепедов давления в рассматриваем скважинах отношением понижений динамических уровней s1 и s2:  (29) (29)Формула (29) позволяет определить понижение s2 динамического уровня в возмущающей скважине, которое необходимо поддерживать, чтобы дебит в реагирующей скважине обратился в нуль при понижении s1 динамического уровня в ней. [9] Рассмотрим пример: Пусть Rk=10км, Rc=10 см, расстояние между скважинами Итак, в условиях рассматриваемого примера для заглушения скважины нужно было бы во вновь пущенной возмущающей скважине снизить динамический уровень почти в три раза больше, чем в реагирующей. Более трудной задачей является определение дебитов скважин при вытеснении нефти. Рассмотрим пример решения такой задачи: Исходные данные: Расстояние между скважинами – 200 м, 100 м Проницаемость – 0,3 мкм Радиус контура питания – 500 м Динамическая вязкость нефти – 5 мПа*с Толщина пласта – 10 м Изменение дебита возмущающей скважины – 20 м/сут , 50 м/сут , 100 м/сут , 200 м/сут Построить график изменения давления на забоях скважин в зависимости от дебита. Решение: 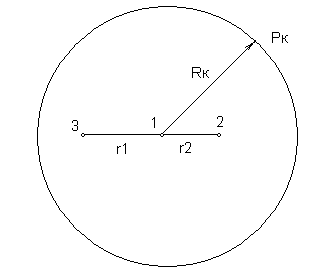 Рисунок 10– Расположение скважин и контур питания. Будем исходить из формулы для потенциала при работе группы скважин Учитывая, что скважины расположены вдали от контура питания, в точке, помещённой на контуре питания, получим  (1) Помещая точку М на забой второй скважины, будем иметь Вычитая из (1) (2) и заменяя Получим: Помещая точку М на забой третьей скважины, будем иметь Вычитая из (1) (3) и заменяя 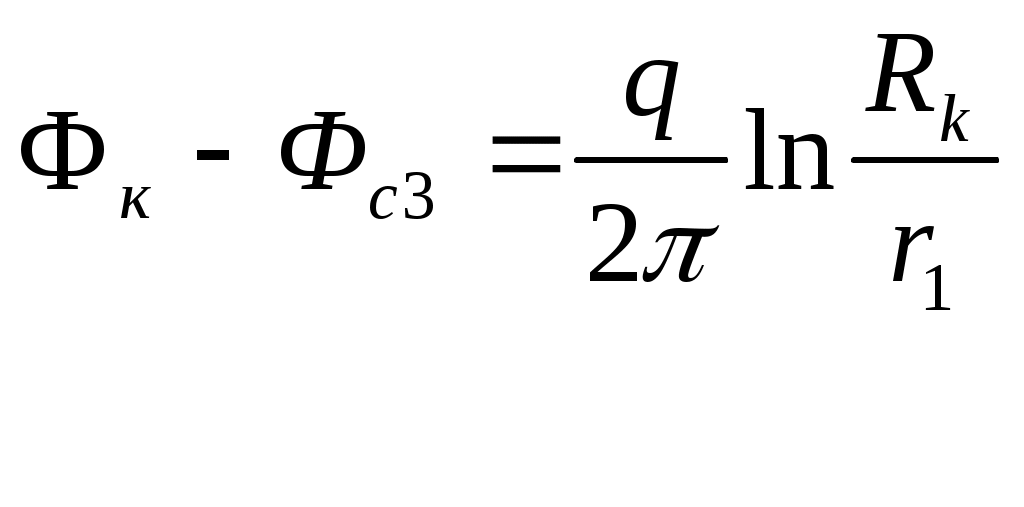 Получим:  Найдём дебит скважины: Q=q*h Таблица 1 – Результаты вычислений
Таблица 2 – Результаты вычислений
Далее построим график изменения давления на забоях скважин в зависимости от дебита. 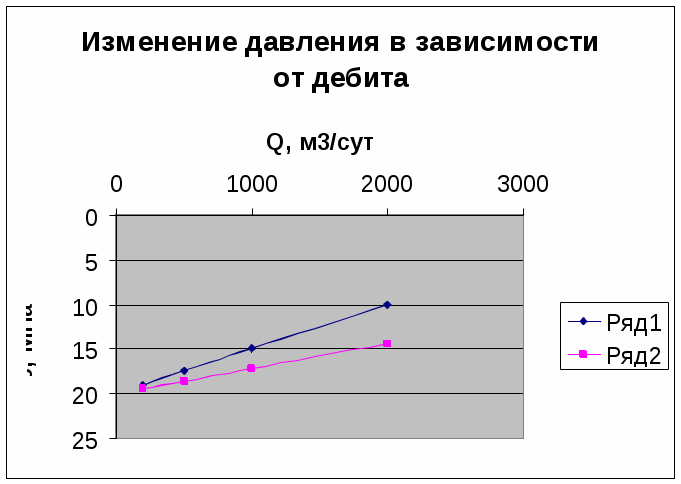 Рисунок 11 – График изменения давления на забоях скважин в зависимости от дебита. Условные обозначения: ряд 1 – скважина 2; ряд 2 – скважина 3. ЗАКЛЮЧЕНИЕ В рассматриваемой курсовой работе по дисциплине подземной гидромеханики изучена тема: «Изучение интерференции совершенных скважин при фильтрации нефти и газа». В данной работе мы, путём анализа научно-технических работ и материалов, мы изучили основные принципы и задачи интерференции совершенной скважины, а также привели математические уравнения, описывающие данные задачи. Немаловажными были вопросы практического применения методик, отвечая на него, мы привели примеры численных расчетов и графические решения различных задач, которые используются на практике, непосредственно во время эксплуатации месторождения. Явление интерференции (взаимодействия) скважин заключается в том, что под влиянием пуска, остановки или изменения режима работы одной группы скважин изменяются дебиты и забойные давления другой группы скважин, эксплуатирующих тот же пласт. На основании исследований, проведенных в данной работе относительно притока жидкости к скважине или батареям скважин; можно сделать следующие выводы: -при решении задач расчета дебитов рядов скважин в залежах нефти и газа нужно учитывать, что при работе скважин наблюдается их взаимное влияние друг на друга - интерференция скважин. Это влияние выражается в том, что при вводе в эксплуатацию новых скважин суммарная добыча из месторождения растет медленнее, чем число скважин; -задачи интерференции скважин имеют важнейшее значение при рассмотрении естественного или искусственного создаваемого (нагнетанием воды) водонапорного зажима; -результат интерференции сказывается в том, что при введении в эксплуатацию ряда скважин (работающих в одинаковых условиях) прирост суммарного дебита уменьшается. Кривая зависимости суммарного дебита от числа скважин с ростом становится все более пологой. Чем ближе расположены скважины друг к другу, тем сильнее сказывается эффект интерференции и тем меньшим оказывается суммарный эффект; -при разработке нефтяных месторождений плотность сетки скважин, а также их взаимное расположение (в виде рядов, круговых батарей, прямоугольной сетки и т.д) играет первостепенную роль для определения суммарной добычи; -большое влияние оказывает на суммарную добычу расстояние от действующих скважин до контура области питания или до цепочки нагнетательных скважин. При приближении нагнетательных скважин к добывающим эффект взаимодействия между ними уменьшается, и их дебиты увеличиваются. Таким образом обобщая вышеизложенные выводы можно сказать: что приближая нагнетательные скважины к добывающим, можно добиться увеличения добычи при более тесном расположении скважин. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ Б.Б. Пыхачев. "Подземная гидравлика".– М.: Недра,1990. – С. 103–105. Басниев К.С.,. Подземная гидромеханика: Учебник для вузов //. Кочина И.Н., Максимов В.М – М.: Недра, 1993. . – 402 с Бузинов С.М.,. Исследование нефтяных и газовых скважин и пластов. // Умрихин И.Д – М.: Недра 1984– С. 87–92. В.Д. Лысенко. " Разработка нефтяных месторождений. Проектирование и анализ".– М.: Недра 1998. – . – 103 с В.Н. Щелкачев. "Подземная гидравлика".– М.: Недра.,2001. – С. 17–33. В.С.Бойко. "Разработка и эксплуатация нефтяных месторождений".– М.: Недра 1990. – С. 11. Евдокимова В.А., Сборник задач по подземной гидравлике. // Кочина И.Н. – М.: Недра 1979, . – 168 с. Желтов Ю.П. Механика нефтегазового пласта, М: Недра, 1975[8] К.М. Донцова. "Разработка нефтяных месторождений". – М.: Недра 1977. – С. 11–23. К.С. Басниев. "Подземная гидравлика". // А.М. Власов. – М.: Недра 1995– С. 85–92. Куштанова Г.Г. Подземная гидромеханика. Учебно-методическое пособие для магистрантов физического факультета по направлению «Радиофизические методы по областям применения»/ – М.: Казан.(Приволж.) федер. ун-та, 2010, – С. 100–110. Петрушин Е.О., Интерференция совершенной скважины // Арутюнян А.С., Ассаиди М.Б. // ЦДНГ1 ОАО «Печоранефть» 2005 // - URL: https://elibrary.ru/item.asp?id=32381511& (дата обращения: 20.06.2020) Пыхачев Г.Б.,. Подземная гидравлика. // Икаев Р.Г М: Недра. 1973 – С. 67–73. Пятибрат В.П. Подземная гидромеханика. Учебное пособие. – М.: - Ухта: УГТУ, 2002. – С. 50–52. П.Я. Полубаринова Развитие исследований по теории фильтрации в СССР.. – М: Наука, 1969 Чарный И.А Подземная гидромеханика. – М.: Гостоптехиздат, 1963.-– С. 145-150. |
