Консаекты уроков по функциональной грамотности. Й класс Математическая грамотность

• Название: Й класс Математическая грамотность
• Анкор: Консаекты уроков по функциональной грамотности
• Дата: 17.03.2023
• Размер: 0.74 Mb.
• Имя файла: 6kl_Konspekty_urokov_po_FG.docx
• Тип: Документы; #998073
• страница: 1 из 4

6. й класс Математическая грамотность

6мг-4 Геометрические задачи на построение

и на изучение свойств фигур: геометрические фигуры на клетчатой бумаге, конструирование

Составила Алинская Лариса Валентиновна, МКОУ Железнодорожная СОШ № 121

Цели: знакомство обучающихся с различными задачами на раз- резание и складывание фигур; формирование пространственного воображения обучающихся.

Задачи:

• 
  рассмотреть различные способы решения геометрических за- дач на разрезание и складывание фигур на плоскости; позна- комить с задачами на клетчатой бумаге и их решением;
  
• 
  развивать геометрические навыки, применительно к практи- ческим ситуациям, формулировать и аргументировать соб- ственную позицию, работать с геометрическими фигурами, телами.
  

Планируемые результаты:

Предметные и метапредметные: применять математические зна- ния для анализа практических ситуаций, умение строить математи- ческие модели практических ситуаций.

Личностные:видеть возможность применения математических знаний.

Ход урока

1. 
   Организационный момент.
   

Приветствие. Проверка готовности учащихся к уроку.

2. Актуализация знаний

Учитель: Чтобы нам плодотворно сегодня потрудиться, немного разомнемся.

Задача 1. Разминка для головы: переставьте одну спичку так, чтобы равенство было верным.

Ученики предлагают свой вариант.

3. Основной этап.

Учитель: Тема нашего урока связана с применением геометрии в повседневной жизни.

Есть ли у вас примеры из жизни, когда вам пригодились знания по геометрии?


Посмотрите на картинку и назовите геометрические понятия, которые вы видите (угол, прямые). Какие свойства вы вспомните, связанные с ними?

Ученики: Две ветки — параллельные прямые, ствол и ветки ра- стут под углом и т.д.

Любой садовод использует эти понятия при весенней обрезке плодовых деревьев. Более того, ему необходимо уметь измерять углы.

Задача 2. Оказывается, угол, который образует ветвь со стволом плодоносящего дерева (он называется углом отхождения), влияет на плодоношение. Оптимальным углом отхождения скелетных вет- вей считается угол 50–60°. Ветви с углом отхождения менее 45° и более 80° рекомендуется удалять.

Учитель: Что нам нужно сделать, чтобы определить, какую ветку нам нужно удалить.

Ученики: Нужно узнать, сколько градусов каждый угол. Учитель: Что нам для этого понадобится?

Ученики: Для определения угла нам нужны линейка и транспор- тир.

Ученики с помощью транспортира по фотографии определяют, какие ветви нужно удалять (углы менее 45° и более 80°). Их задача, кроме измерения угла, наметить порядок действия.

В беседе формируется порядок действия по измерению угла по фотографии. Ученики приводят аргументы, почему некоторые углы по фотографии нельзя определить достоверно.

Учитель: Есть ещё много ситуаций в жизни, где требуется по- строить модели, связанные с геометрическими понятиями. Догада- лись, о каких задачах идёт речь?

Известно, что с этими задачами, очевидно, столкнулся ещё пер- вобытный человек, когда пытался раскроить шкуру убитого зверя, чтобы сшить себе одежду. Любой портной до сих пор решает такие задачи, чтобы сэкономить ткань. Решения многих простых подоб- ных задач были найдены ещё древними греками.

Ответы детей.

Да, конечно, речь идёт о задачах на разрезание. Задачи на разре- зание или на перекраивание фигур возникли в глубокой древности. Уже в VII в. до н.э. в Индии в книге «Правила верёвки» рассматри- ваются задачи на перекраивание фигуры, состоящей из двух квадра- тов, в равновеликий ей квадрат и перекраивание прямоугольника в квадрат. Первый письменный источник с подобными задачами от- носится к Х веку — это фрагменты трактата персидского астронома Абул-Вефа, жившего в Багдаде. Профессиональные математики все- рьёз занялись задачами на разрезание ближе к середине XIX века.

Задача 3. Разрежьте прямоугольник, длина которого равна 9 клеткам, а шири- на 4, на две равные части так, чтобы из них можно было сложить квадрат.

Решение:

Задача 4. Постройте прямоугольный треуголь- ник, у которого две стороны равны. Разрежьте его на три неравные части, из которых можно было бы со- ставить два равных квадрата.

Решение:

Если вспомнить вид коврика для раскройки ткани или разделки теста или обратную сторону клейкой декоративной пленки (мас- штабная клетка), та на ум приходят целый класс задач — задачи на нахождении площади фигуры на клетчатой бумаге. Этот же приём вы будете использовать на уроках физики.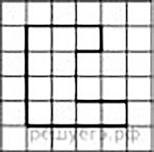

На клетчатой бумаге с размером клетки 1 × 1 изображена фигура. Найдите её площадь.

Ваши варианты. Как можно решить данную задачу?

Ученики предлагают свои варианты. Сконструируйте аналогичную задачу, реше-

ние которой будет полезно в жизни (например, покупка линолеума для пола сложной формы при небольших средствах).

4. Подведение итогов.

Учитель: Подведите итог. Что вы делали на уроке? Какие задачи вам показались неизвестными, интересными, полезными?

Итак, мы часто встаём перед задачами в жизни, которые от нас требуют применения математических умений и навыков, знаний формул, правил вычислений. Их важность подчеркивается тем, что на итоговом экзамене эти типы задач встречаются систематически.

5. 
   Домашнее задание.