ответы основы информоционных систем. ОИС отв. Жйелер теориясыны негізгі элементтерін натылап крсетііз. Жйені асиеттерін атаыз жне р асиетіне сипаттама берііз
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
Кодтау мақсаты – тасымалдауға немесе ақпаратты сақтауға кететін шығындарды азайту. Есептің шешімі жіберілетін мәліметтер ағымынан артық ақпаратты «жою» деп түсіндіруге болады. Жіберілетін ақпаратты байланыс каналдары арқылы жіберу кезіндегі бөгеуілдер мен бұрмалаудан қорғау немесе ақпаратты сақтау мақсатында кодтау қарастырылады. Тиімді байланыс жүйесін құру үшін жіберілетін ақпараттың көлемін азайту мақсатында алдымен хабарламадағы артықты жоюға, содан кейін ақпаратты қателіктерден қорғау үшін артықтықты енгізу керек. Шумен күресу теорияcының ең маңызды идеясы мынада, байланыс каналы бойынша берілген код артықтық (избыточность) болуы керек. Код артықтығы – бұл берілетін ақпараттың немесе деректердің бірнеше рет қайталануы. Код артықтығы өте үлкен бола алмайды. Себебі бұл байланыстың қымбаттауына және кешеуілдеп жетуіне ықпал етеді. Кодтау теориясы оңтайлы кодты алуға тырысады: берілетін ақпарат артықтығы мүмкіндігінше минимум, ал қабылданған ақпарат нақтылығы максимум болуы тиіс. 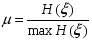 Энтропиясы үлкен (максимум) хабарламалар берілген ақпараттың символының санына қатысты оңтайлы болып табылады. Сандық бағалау өлшемі сығу коэффициентімен бағаланады: Энтропиясы үлкен (максимум) хабарламалар берілген ақпараттың символының санына қатысты оңтайлы болып табылады. Сандық бағалау өлшемі сығу коэффициентімен бағаланады:мұндағы Н(ξ) – нақты хабарлама энтропиясы, max H(ξ) – нақты хабарламаға сәйкес оңтайлы энтропия. 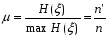 Артықтықты сандық бағалау өлшемі артықтық коэффициенті болып табылады. 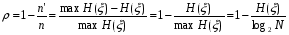 Символдарды беру ықтималдықтары: Ақпарат саны мен артықтығын табу керек. Шешуі. Шеннон формуласы бойынша Артықтық анықтамасы бойынша Канал коды деп алфавит үстіндегі A={xm}, m=1,…,M , A Xn кез келген тізбектер жиыны айтылады. Тізбектердің өзі кодтық сөз, олардың ұзындығы nкод ұзындығы, тізбектер саны М код қуаттылығы деп аталады, ал R = logM / n мәні код жылдамдығы деп аталады. Код жылдамдығы бит канал символымен өлшенеді. Жекелей жағдайда M=2k болған кезде әрбір кодтық сөзге k ақпараттық символдан тұратын тізбекті сәйкестендіруге болады (k бит). Оларды жіберу үшін n ұзындықты кодтық сөз қолданылады. Канал символына биттерді жіберу жылдамдығы R =logM / n = k / n бит/символын құрайды. Өзара ақпарат. Орташа өзара ақпарат. Байланыс каналдарын меңгеру барысында канал кірісінде бақыланатын символдар бойынша хабарламаны жіберу туралы ақпарат алу мүмкіндігі туындайды. X және Y дискретті ансамбльдердің XY = {(x, y), p(x, y)} берілген көбейтіндісі үшін y ∈Y шығыс символдарында болатын кіріс ансамблінің x ∈ X элементтері туралы ақпаратты сандық түрде өлшеу керек болса, онда мұндай ақпаратқа сәйкес келетін шама (x, y)∈ XY кез келген жұптары үшін I (x; y) = I (x) − I (x | y) арақатынасымен анықталатын өзара ақпарат бар болады. Өзара ақпараттың қасиеттері: 1. Симметриялық: I (x; y) = I ( y; x) . 2. Егер x және y тәуелсіз болса, онда I (x, y) = 0 X және Y ансамбльдері арасындағы орташа өзара ақпарат деп I (X;Y) = M[I (x; y)] өлшемі айтылады. Орташа өзара ақпаратты ортақ үлестірім ықтималдығы арқылы өрнектейтін формула Орташа өзара ақпараттың қасиеттері 1 қасиет. Симметриялық I (X;Y) = I (Y; X ) . 2 қасиет. Теріс болмаушылық: I (X;Y) ≥ 0. 3 қасиет. X және Y ансамбльдері тәуелсіз болған кезде, тек сол кезде ғана I(X;Y)=0 тепе-теңдігі орын алады. 4 қасиет. I (X;Y) = H(X ) − H(X | Y) = = H(Y) − H(Y | X ) = = H(X ) + H(Y) − H(XY) . 5 қасиет. I (X;Y) ≤ min{H(X ),H(Y)}. 6 қасиет. I (X;Y) ≤ min{log | X |, log | Y |}. 7 қасиет. Өзара ақпарат I (X;Y) – p(x) үлестірім ықтималдығының дөңес ∩ функциясы. 8 қасиет. Өзара ақпарат I (X;Y) – p(у|x) шартты үлестірімінің ойыс ∪ функциясы. Хемминг кодындағы қателікті табу алгоритмін түсіндіріңіз. Хэмминг шекараларын көрсетіңіз. Хэмминг кодындағы қателікті табуға мысал келтіріңіз. Хэмминг коды - өткен ғасырдың 1940 жылдарында Ричард Хемминг әзірлеген бір қатені түзетуге және қос қателерді түзеуге мүмкіндік беретін блоктық код. Басқаша айтқанда, бұл қандай да бір ақпараттық хабарламаны белгілі бір жолмен кодтауға және (мысалы, желі бойынша) жібергеннен кейін осы хабарламада қандай да бір қате пайда болғанын анықтауға (мысалы, кедергілерге байланысты) және мүмкіндігінше, осы хабарламаны қалпына келтіруге мүмкіндік беретін алгоритм. Сондай-ақ, осы алгоритмнің неғұрлым жетілдірілген модификациялары бар екенін атап өткен жөн, олар көптеген қателерді анықтауға мүмкіндік береді (және мүмкін болса түзету). Бірден айта кету керек, Хэмминг коды екі бөліктен тұрады. Бірінші бөлім белгілі бір орындарда бақылау биттерін (ерекше түрде есептелген) енгізе отырып, бастапқы хабарламаны кодтайды. Екінші бөлім кіріс хабарын алады және бақылау биттерін қайта есептейді (БІРІНШІ БӨЛІМ сияқты алгоритм бойынша). Егер барлық жаңадан есептелген бақылау биттері алынғандармен сәйкес келсе, онда хабарлама қатесіз алынды. Әйтпесе, қате туралы хабарлама шығады және мүмкін болса қате түзетіледі. Егер кодталатын ақпараттық блоктың ұзындығы m - бит болса. Кодтау үшін пайдаланылатын басқару биттерінің саны k, одан кейін кодталған блок ұзындығы: n = m + k биттерге ие болады. Осы ұзындықтың әр блогы үшін, қателігі бар әр түрлі комбинациялары мүмкін. Осылайша, берілген әрбір блок үшін блок болуы мүмкін n - блоктары бар бір қате және бір блок қатесіз. Сондықтан, бірден көп қате болмайтын әр түрлі кодталған блоктардың максималды саны болады: 2m(n+1), где n = m+k 22-сұрақ мысалының жалғасы Жеті элементтен тұратын екілік деректерді кодтаудың мысалын қарастырайық: 1001101. 1. Сынақ биттерінің қажетті санын анықтаңыз. Есептеу мынадай формула бойынша жүргізіледі: k = 2k – m – 1 мұнда k - бақылау биттерінің саны, м - ақпараттық бит саны. Биттердің саны бүтін сан болуы керек болғандықтан, осы теңдеуді пайдалана отырып есептелген k ең жақын бүтін санға дейін дөңгелектелуі керек. Есептеу нәтижесі төменде көрсетілген:  Осылайша, бақылау биттерінің саны - 4. 2. Алынған кодталған реттіліктегі бақылау биттерінің орналасуын анықтаңыз. Біз И символы бойынша ақпараттық биттерді және П таңбасы бойынша бақылау биттерін белгілейік. Бұл таңбалардың жанындағы индекс жүйелі түрде жүйелі реттік нөмірді білдіреді. Басқару биттері екі позицияға ие болады: 20, 21, 22, 23 => 1,2,4,8. Алынған дәйектілікке ақпарат пен тексеру биттерін орналастыру келесідей болады: 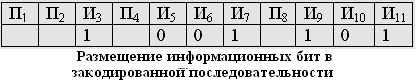 Тексеру биттерінің мәндерін анықтау қалады. 3. Тексеру биттерін басқаратын топтарды анықтаңыз. Ол үшін ақпараттық биттердің сериялық нөмірлерін екеуінің қуатына қарай бөлшектеңіз: И3: 3 = 20 + 21 = 1 + 2 => И3 ақпараттық биті П1 және П2 бақылау биттері арқылы тексеріледі. И5: 5 = 20 + 22 = 1 + 4 => И5 ақпараттық биті П1 и П4 бақылау биттері арқылы тексеріледі. И6: 6 = 21 + 22 = 2 + 4 => И6 ақпараттық биті П2 и П4 бақылау биттері арқылы тексеріледі. И7: 7 = 20 + 21 + 22 = 1 + 2 + 4 => И7 ақпараттық биті П1, П2 и П4 бақылау биттері арқылы тексеріледі. И9: 9 = 20 + 23 = 1 + 8 => И9 ақпараттық биті П1 и П8 бақылау биттері арқылы тексеріледі. И10: 10 = 21 + 23 = 2 + 8 => И10 ақпараттық биті П2 и П8 бақылау биттері арқылы тексеріледі. И11: 11 = 20 + 21 + 23 = 1 + 2 + 8 => И11 ақпараттық биті П1, П2 и П8 бақылау биттері арқылы тексеріледі. 4. Бақылау биттерінің мәнін есептейміз. Ол үшін барлық бақылау биттері үшін топтарды анықтаймыз, оларды екі модуль бойынша ойластырамыз, ал нәтижесін тиісті бақылау биттеріне жазамыз (бірліктердің нақтылығына дейін топтарды толықтырайық)): П1 = И3 + И5 + И7 + И9 + И11 = 1 + 0 + 1 + 1 + 1 = 0 П2 = И3 + И6 + И7 + И10 + И11= 1 + 0 + 1 + 0 + 1 = 1 П4 = И5 + И6 + И7 = 0 + 0 + 1 = 1 П8 = И9 + И10 + И11 = 1 + 0 + 1 = 0 Осылайша, кодталған жүйе келесідей болады:  Тексеру разрядтарымен бақыланатын барлық топтарды бірліктердің жұптығын тексереміз: П1: П1 + И3 + И5 + И7 + И9 + И11 = 0 + 1 + 0 + 1 + 1 + 1 = 0 П2: П2 + И3 + И6 + И7 + И10 + И11 = 1 + 1 + 1 + 1 + 0 + 1 = 1 П4: П4 + И5 + И6 + И7 = 1 + 0 + 1 + 1 = 1 П8: П8 + И9 + И10 + И11 = 0 + 1 + 0 + 1 = 0 Бірліктердің анықтығын тексеру П2 және П4 бақылау биттері топтары үшін өтпейтіндіктен, қате осы топтарға тиесілі биттерде кездеседі. Хемминг алгоритмі тек бір қатені түзетуге мүмкіндік береді, сондықтан тек бір қате орын алуы мүмкін деген болжамға сүйене отырып, ақауды іздейміз. Егер бұл болжам дұрыс емес болса, онда деректерді түзетудің барлық әрекеттері ақпараттың қосымша бұрмалануын алып келеді. Мәселен, егер қате бір ғана болса, онда ол екі топқа тиесілі биттердің бірінде болуы керек. Бұл и6 және И7 биттері. Дәл қандай Битте қате болғанын анықтау үшін, нақтылыққа тексеру сәтті өткен топтарға жүгінеміз, демек, осы топтарда барлық биттер дұрыс. Көріп отырғаныңыздай, жарамды топтардың біріне бит И7 тиесілі, демек, ол адал. Осылайша, қате И6 битінде орын алғаны анық, және оның мәнін түзете отырып, біз қабылданған деректерді қалпына келтіреміз. Жоғарыда сипатталған алгоритмді пысықтауға болады және ол тек бір рет қателерді түзетіп қана қоймай, екі есе тіркеуін де жасауға болады. Бұл үшін ақпараттық деректер кодталғаннан кейін алынған кодқа бірліктердің нақтылығына дейін толықтыратын тағы бір разряд жазылады. Егер қателердің саны екіден көп емес деп болжасаңыз, онда: - Егер барлық бақылау топтарында бірліктер саны бірдей болса және бірліктердің жалпы саны болса, деректер дұрыс. - Кейбір бақылау топтарында бірліктер саны тақ болса және бірліктердің жалпы саны тақ болса, бір реттік қате пайда болды. - Барлық бақылау топтарында бірлік саны бірдей болса және бірліктердің жалпы саны тақ болса, қосымша бақылау битіндегі қате. - Егер кейбір бақылау топтарында бірліктер саны тақ болса және бірліктердің жалпы саны тең болса, қос қате. Көріп отырғанымыздай, Хэмминг қателерді түзету алгоритмі өте қарапайым және сенімді. Сонымен бірге кодының тиімділігі ақпараттық блоктарды көбейту арқылы артады. Мәселен, 7 биттік деректерді кодтау үшін артықшылығы 57% -дан асады, кодтау үшін 256 бит, артықшылық 3,5%, ал 1024-1% болады. Хэмминг кодтау алгоритмі өте танымал және ақпаратты беру және сақтау сенімділігін едәуір жақсарта алады. Әсіресе, үлкен деректер блоктарын кодтау кезінде пайдалы. Бұл алгоритмді жүзеге асырудың көптеген тәсілдері бар. Хэмминг шекарасы Кодтау теориясында Хамминг шекарасы кез келген блоктық код параметрлерінің ықтимал мәндерінің шекараларын анықтайды. Сондай-ақ сфералық орауыш шекарасы деп те аталады. Хамминг шекарасына жететін кодтар керемет немесе жақын оралған деп аталады. Формулировка Пусть Aq (n, d) обозначает максимально возможную мощность {\displaystyle q}q-ичного блокового кода {\displaystyle C}C длины {\displaystyle n}n и минимального расстояния {\displaystyle d}d ({\displaystyle q}q-ичный блоковый код длины {\displaystyle n}n — это подмножество слов 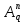 с алфавитом Aq , состоящим из q элементов). с алфавитом Aq , состоящим из q элементов).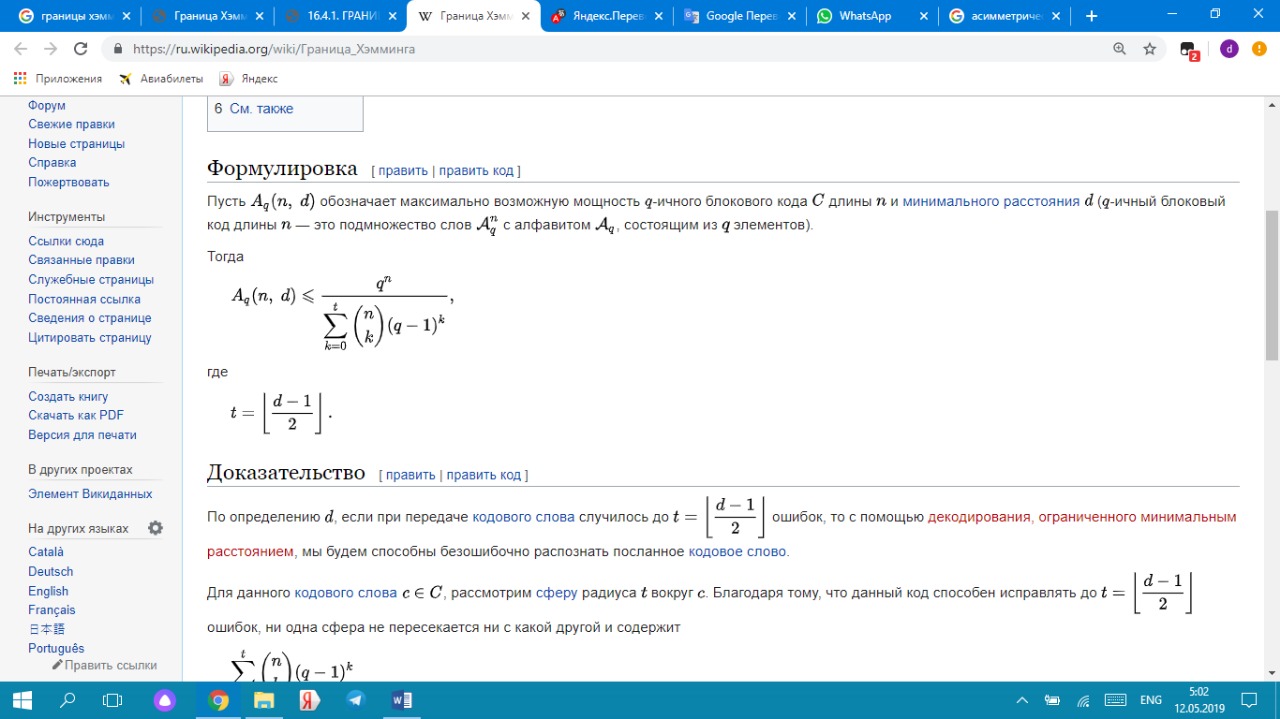 |
