ответы основы информоционных систем. ОИС отв. Жйелер теориясыны негізгі элементтерін натылап крсетііз. Жйені асиеттерін атаыз жне р асиетіне сипаттама берііз
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
Хэмминг шекарасы Кодтау теориясында Хамминг шекарасы кез келген блоктық код параметрлерінің ықтимал мәндерінің шекараларын анықтайды. Сондай-ақ сфералық орауыш шекарасы деп те аталады. Хамминг шекарасына жететін кодтар керемет немесе жақын оралған деп аталады. Формулировка Пусть Aq (n, d) обозначает максимально возможную мощность {\displaystyle q}q-ичного блокового кода {\displaystyle C}C длины {\displaystyle n}n и минимального расстояния {\displaystyle d}d ({\displaystyle q}q-ичный блоковый код длины {\displaystyle n}n — это подмножество слов 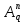 с алфавитом Aq , состоящим из q элементов). с алфавитом Aq , состоящим из q элементов).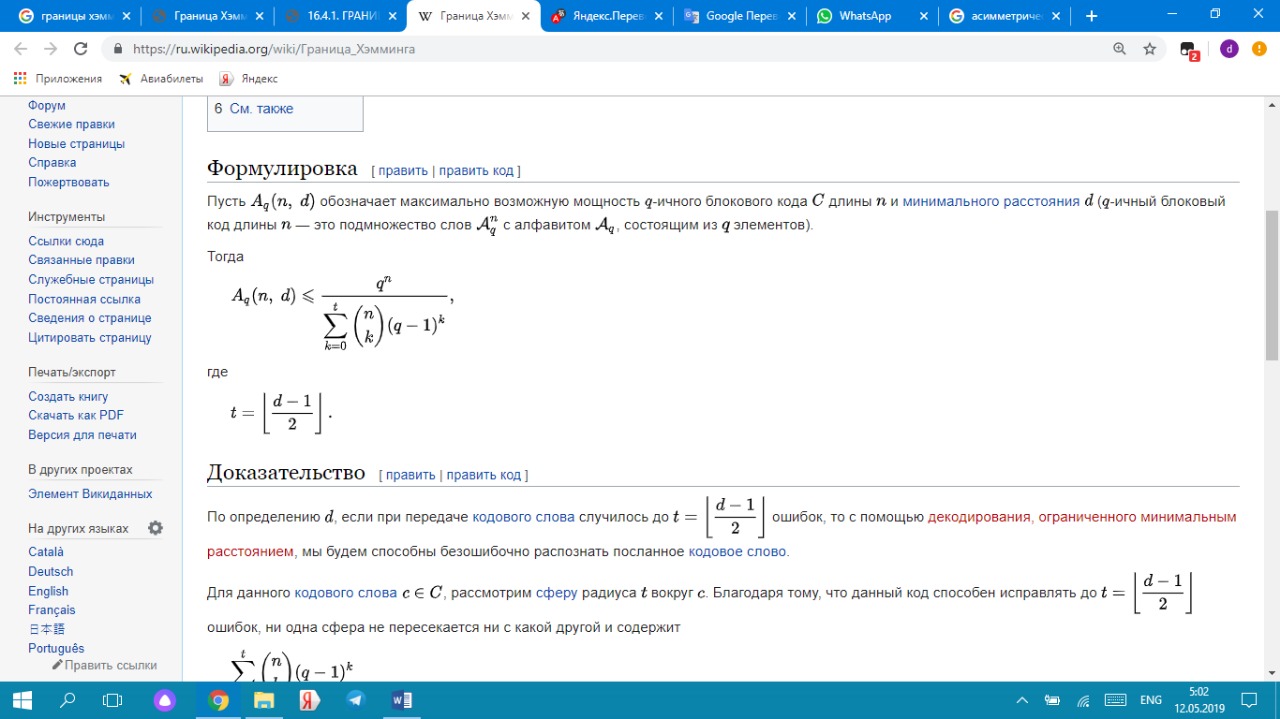 Циклдік кодтарға математикалық кіріспе. Циклдік кодтар анықтама беріңіз. Мысал келтіріңіз. Кең тараған сызықты кодтар - циклдік, оларда рұқсат етілген комбинация символдарының циклдік орналасуы рұқсат етілген кодтық комбинацияны береді. Бұл егер кодтық комбинация Циклдік кодтар жүйелік кодттар санына жатады, ондағы әрбір комбинация ақпараттық k және бақылаушы m символдар нақты бір орында болатындай етіп, өздігінен (блок түрінде) кодталады. Тәжірибелік кез келген қателікті айтарлықтай аз артықшылық кезінде басқа кодтармен салыстыру бойынша табу және жөндеу мүмкіндігі, сондай ақ аппаратураны жүзеге асыру схемасының қарапайымдылығы, кодтау сияқты декодтауда бұл коды кең қолданылатын қылды. Циклдік кодтар жүзеге асыруда қарапайым: көбейту, қосу және бөлу операциялары жылжуды тіркеу кезінде жүзеге асады, бұл кодтар жоғары түзетуші қабілетке ие, циклдік кодты кез келген алдын ала берілген кодтық қашықтық тапсырмамен қалыптастыруға болады. Қазіргі уақытта қатені түзету аппаратураларында негізінен циклдік кодтарды қолданады. Практика жүзінде ең көп таралған сызықтық кодтар классына жататын циклдік кодтар. Бұл атау осы кодтардың негізгіқасиетінен шығады: егер де қайсібір кодтық комбинация циклдік кодтқа жататын болса, онда циклдік ауыстырып қойғаналғашқы комбинациядан шыққан комбинация (циклдік жылжу), сондай –ақ осы кодқа жатады: a1,a2,...,an-1,an; → an,a1, a2,..., an-1 Барлық рұқсат етілген циклдік кодтар комбинацияларының екінші қасиеті олардың бір таңдалған, өңдіруші деп аталатынполинемге қалдықсыз бөлінуі. Осы кодтардағы қатенің синдромы деп, қабылданған кодтық комбинация өңдіретін полинемге бөліну кезіндегіқалдықтың қалуын айтады. Осы қасиеттерді кодтарды құрастыру кезінде, кодалаушы және декодалаушы құрылғыларда, сонымен қатар қателердітабу үшін және түзетү үшін қолданылады. Кодтықкомбинациясыныңкөпмүшетүріндекөрінісі Циклдік кодтарды және олардың құрылысын көпмүше арқылы шығару ыңғайлы (немесе полиндер арқылы). Циклдік кодтар теориясында кодтық комбинацияларды көбіне полином түрінде ұсынады. Осылайша, n-элементті кодтықкомбинациясын (n-1) дәрежесіндегі полином түрінде көрсетуге болады: An-1(x)=an-1xn-1+an-2xn-2+...+a1x+a0 мұндағы ai={0,1} ескере кету керек ai=0 комбинацияның нольдік элементіне сәйкес келеді, ал ai=1 – нольдік емес. 4-элементті белгілі комбинация үшін полиномдар: 1101↔ A1(x)=x3+x2+1 1010 ↔ A2(x)=x3+x Полиномдарға қолданылатын амалдар Циклдік кодтың комбинациясын құру кезінде көбіне көпмүшені қосу мен бір көпмүшені басқа көпмүшеге бөлуоперацияларын қолданады.Осылайша: A1(x)+A2(x)=(x3+x2+1)+(x3+x)=x2+x+1, x3+x3=(1* 1)x3=0 Полиномдар коэффициентіне қолданылатын амалдар (қосу және көбейту) модуль екі көмегімен іске асатынын ескерекеткен жөн. Бөлу операциясын келесі мысалда қарастырамыз: 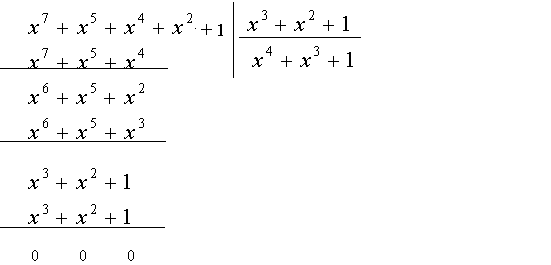 Бөлу әдеттегідей іске асады, тек азайту модуль екі бойынша қосумен алмастырылады. Қарапайым код комбинациясынан рұқсат етілген циклдік код комбинациясын алу алгоритмі P(x)=ar-1xr+ar-2xr-1+...+1 полиномы берілген болса, кодтың түзетуші қабілетін анықтайтын және r тексеру разрядтарыныңсаны, және де қарапайым k-элементті кодтың бастапқы комбинациясы көпмүше түрінде берілсе. Циклдік кодтың рұқсат етілген комбинацияның (n, k) анықтау керек . 1. Көпмүшені бастапқы комбинация кодына көбейтеміз xr: Ak-1(x)*xr 2. Бастапқы информациондық комбинацияны рұқсат етілген комбинацияға толықтыратын, тексерілетін разрядтардыанықтаймыз, ол үшін жоғарыда айтылып кеткен пунктегі полинмен алынған көбейтінді сияқты бөлгінге дейінгі қалдықтүрінде аламыз: 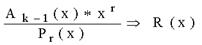 3. Шеше келе циклдік кодтың рұқсат етілген комбинациясы былай анықталады: An-1(x)=Ak-1(x)xr+R(x) Қабылдаған кодтық комбинацияның қатесін анықтау үшін оны өндіретін полинге бөлу жеткілікті. Егер қабылданғанкомбинация – рұқсат етілген болса, онда бөлінген қалдық нөльдік болады. Нөлдік емес қалдық- қабылданған комбинациядақате бар болуын айтады. Кейбір жағдайларда қалдыққа (синдаром) қарап қатенің мінезін қорынтындауға болады, оныңтұрған орнын және қатені түзетуге болады. Циклдіккодтағықателіктікразрядтыанықтау A(x) – сәйкес таратылған кодтық комбинация көпмүшесі болсын. H(x)- сәйкес қабылданған кодтық комбинациякөпмүшесі болсын. Онда берілген көпмүшелерді модуль екі бойынша қосу келесі қателік көпмүшесін береді: E(x)=A(x) * H(x) Бір реттік қателік кезінде E(x) қателіктік разрядқа сәйкес келетін тек бір мүше болады. H(x) қабылданған көпмүшесін өңдіруші Pr(x) бөлу кезіндегі қалдық сәйкес E(x) қателік көпмүшесін Pr(x) бөлгендегіқалдыққа тең: 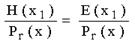 Қателікті анықтау алгоритмі n-элементті (n=k+r) комбинациялары бар делік, сонда: 1. [1000000000] үлкен разрядындағы қателікке сәйкес E(x)-ті Pr(x) өңдіруші полиномына бөлудегі қалдықты табамыз: 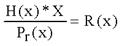 2. Алынған H(x) көпмүшесін Pr(x) бөлеміз де R(x) ағымдық қалдығын аламыз. 3. R0(x) мен R(x) салыстырамыз. Олар тең болса, онда қателік үлкен разрядта кеткен. Егер "жоқ" болса, онда алынған полином дәрежесін X-ке арттырамыз да тағы да бөлеміз: 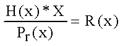 4. Тағы да шыққан қалдықты R0(x)-пен салыстырамыз. Егер олар тең болса, онда қателіктер екінші разрядта. Егер жоқ болса, онда H(x)x2 көбейтеміз және R(x) пен R0(x) өзара тең болғанша операцияларды қайталай береміз. Қателік H(x) дәрежесі көтерілген саны плюс бір санына сәйкес разрядта болады. Мысал 1. Бірді 1011 жасаушы көпмүшелікке бөлгенде қалдық алу Шешімі: 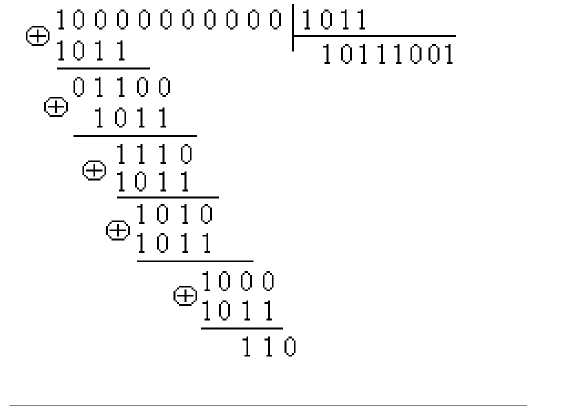 Қалдық: 1) 011 4) 101 7) 100 2) 110 5) 001 8) 011 3) 111 6) 010 9) 110 Сегізден бастап қалдық қайталанады 5.1.3 Жасаушы матрицаларды пайдалану арқылы циклдік кодтарды тұрғызу. Қалдық жасаушы матрица тұрғызу үшін қажет болады. Жасаушы матрицаны тұрғызу элементтері бірді нөлімен жасаушы көпмүшеге К(X) бөлгенде болатын қалдықты ұсынатын бірлік транспонирленген және қосымша матрицнанын пайда болуына апарады. Қосымша матрицаның элементтері транспонирленген бірлік матрицадан оңға жазылады. Дегенмен,бірді нөлмен жасаушы көпмүшелікке бөлгендегі қалдық барлық кезде қосымша матрицаның элементі болуы мүмкін емес, соның ішінде салмағы W≥d0−1, d0 – минимальды кодтық арақашықтық. Қалдық ұзындығы бақылаушы разряд санынан кем болмауы қажет, ал қалдық саны ақпараттық разрядтар санымен тең дәрежеде болуы керек. Жасалушы матрицаның жолдары ізделінді комбинацияның бірінші комбинациясын береді. Қалған комбинациялар жасалынды матрицаның барлық мүмкін тіркестерін модуль 2 бойынша қосқаннан пайда болады. Бөгеуілге төзімді кодтар және оларға қойылатын талаптарды атаңыз. Грей кодының алгоритмін түсіндіріңіз. Мысал келтіріңіз. Сигналдарды беру кезінде сигналдар бөгеуілдердің ықпалына ұшырайды. Бөгеуіл дегеніміз кез-келген кедергі жасатын сыртқы әсерлер немесе ауытқулар, сонымен қатар аппаратураның өзіндегі сигналдардың бұрмалануы (аппаратурадағы кедергілер). Бөгеуілдер өндірістік, атмосфералық, кездейсоқ, сыртқы және ішкі болады. Мысалы, атмосфералық бөгеуілдерге найзағайды, құйынды, шықты және күн сәулесін жатқызуға болады. Бөгеуілге орнықтылық дегеніміз байланыс каналдарындағы бөгеуілдерге қарамай ақпаратты қабылдауды жүзеге асыратын жүйенің қабілеттілігі. Ақпараттық жүйелерді талдау кезінде жүйенің бөгеуілге орнықтылығының екі түрі ажыратылып көрсетіледі: статикалық және динамикалық. Статикалық бөгеуілге орнықтылық жалған сигналдардың орта санымен бағаланады, ал динамикалық бөгеуілге орнықтылық жалған командалардың орташа санымен бағаланады. Бөгеуілге орнықтылық теориясының негізін қалаған академик В. А. Котельниковтың негізгі еңбектерінің бірі – «Потенциалды бөгеуілге орнықтылық теориясы». В.А. Котельников берілген бөгеуіл кезінде ақпаратты берудің бөгеуілге орнықтылығын потенциалды бөгеуілге орнықтылық деп атады. Ақпаратты берудің әр түрлі нұсқаларын таңдау, ақпаратты берудің әдістері мен алгоритмдерінің бөгеуілге орнықтылығын талдау, ақпаратты берудің оңтайлы тәсілдері мен алгоритмін техикалық түрде жүзеге асыру бөгеуілге орнықтылық теориясының негізгі есептері болып табылады. Жиі қайталанатын бөгеуілдермен күрестің негізгі әдістері: бөгеуілдер деңгейіне қарағанда сигнал деңгейін жоғарылату, қателерді табу және түзету үшін кодтарды тұрғызу. Қазіргі кезде дискретті байланыс каналдарына қызығушылық танытылуда. Бұл жүйелердегі берілетін дискретті хабарламалар кодтауға келеді. Бөгеуілге орнықты кодтың қарапайым кодтан айырмашылығы, байланыс каналдарында рұқсат етілген разрядтар санынын тұратын кодтық комбинациялар беріледі, ал қолданылмаған кодтық комбинациялар рұқсат етілмеген деп аталады. Грей коды-әйтпесе айна коды, ол сондай-ақ, екі «көрші» ( кодталған , яғни лексикографиялық, жинақталған ) код комбинациялары тек екілік сандардағы саннан ерекшеленетін көрінетін код болып табылады. Басқаша айтқанда, аралас код комбинациялары арасындағы Хамминг қашықтығы - 1. Көп жағдайда іс жүзінде рефлексиялық екілік сұр код пайдаланылады , бірақ жалпы жағдайда әртүрлі алфавиттерден алынған сандардағы сандармен белгіленген сұр кодтардың шексіз жиынтығы бар. Көптеген жағдайларда «сұр коды» термині рефлексиялық екілік сұр код ретінде түсініледі. Бастапқыда электромеханикалық қосқыштардың жалған триггерлерден қорғауға арналған. Бүгінгі таңда, Грей кодтары байланыс жүйелеріндегі қателерді анықтауды және түзетуді , сондай-ақ басқару жүйелерінде кері байланыс сигналдарын қалыптастыруды жеңілдету үшін кеңінен қолданылады.
Дәлелденген, бірақ анық және неліктен бұл бір емес. G [i] = b [i + 1] ^ b [i] теңдігі g [i] = (b [i + 1]! = B [i]) теңдікіне тең. Яғни, Gray кода, құрылғы 0-1 немесе 1-0 көшу әдеттегі екілік кодта (бірінші көшуді қоса алғанда, 0-ден ең маңызды сан) болатын жерде болады. Мысалы: 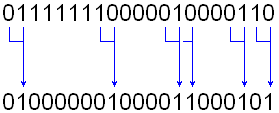 Сур. 1. Тұрақтыекілікденсұркодынатүрлендіру Енді кодта параграфта 2Gray1 функциясының жұмысын сипаттайтын: Яғни, Грейкодқакодберукезінде, біз 1-шіреталғансайын, кодталғаннөмірдіңқалғанбөлігінинвертируем. Келесіқадамдаоныңүлкенбитінжәнет.б. .. және бұл бірдей екенін түсінеді. Осылайша, кодтаудың екі әдісі арасындағы қарым-қатынас нақтыланатын болады. Бұл кездейсоқ емес, алақан емес. Декодтау Сонымен қатар, анықтамалар бойынша жасалуы мүмкін, сондай-ақ: Жоғарыда келтірілген нәтижені қолданамыз: Грей (2 n + x) = 1 | сұр (2 н - 1 - х) Бұл сұр: Грей (1 | екілік (x)) = 1 | сұр (2 н - 1 - х). Сондықтан ең маңызды бит оны қалай алуға болатыны анық. Degray функциясы (Грей (2 n - 1 - x)), әрине, 2 n - 1 - x қайтарады Сондықтан x = 2 n - 1 - дегра (сұр (2 n - 1 - x)) Кодтың келесі элементін алудың міндеті ағымдық сипатқа ие, бірден ақылға келеді. Әзірге екі ықтимал шешімдер болды: бірден серияларды генерациялау немесе екілік кодқа қайта кодтау, біреуіне қосу және Грей кодын қайта кодтау. Екі нұсқа да әдемі емес. Сұр кодекске біреуді қосу үшін алгоритм жасау керек. Сұр кодта әдеттегі екілік кодтағы модульдер 0-1 және 1-0 коэффициенттеріне сәйкес келетіндіктен, сұр кодтағы бірліктердің жұптары екілік кодтағы бірліктер ауқымын анықтайды. 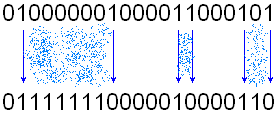 Сур. 2. Көккодтанбинарғадейінтүрлендіру. Бірден анық: Сұр кодта «бірқабатты» бірліктер (ең жоғарыдан бастап санасақ) екілік кодтағы бірліктер ауқымының басталуына және «тіпті» аяғына дейін сәйкес келеді. Сұр кодта бірліктер саны тақ болса, екілік кодтағы бірліктердің соңғы диапазоны санның соңына дейін жалғасады. Яғни екілік кодтың ең аз биті - 1 болып табылады. Яғни, тақ сан Және керісінше, сұр кодында бірдей нөмір болса, нөмір бірдей. Келіңіздер, 1-і қосқанда не болатынын көрейік. Тіпті Осылайша, екілік кодтың кішігірім биі 0, ал екіншісін қосқаннан кейін ол 1 болуға тиіс. Бірақ тағы екі жағдай бар: бұл құрылғы бөлек болуы мүмкін немесе ол бірдей санды біріктіреді. Екі жағдай да 3 және 4-суретте бейнеленген. Жоғарғы жолда - екілік код, төменгі жағында - сұр коды, сұр коды екілік кодта 0-1 және 1-0 өтулеріне сәйкес келеді. Өзгеретін бит сызылған. 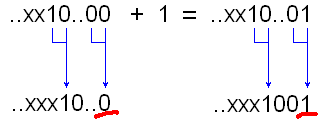 Сур.3. 1-ші нөмірге, 1-нұсқаға қосымша 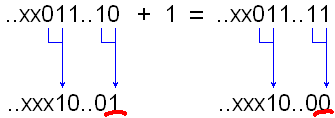 Сур.4. 1-ші нөмірге, 2-нұсқаға қосымша Екі жағдайда да, 1-ден үлкен сандардың сұр кодын алу үшін, сіз жай ғана төменгі регистр битін инверсиялауыңыз керек. Кездейсоқ Сондай-ақ, екі жағдай бірдей негізде: жеке топтағы жаңа бөлімше болады немесе бар болғандардың біріне қосылады. 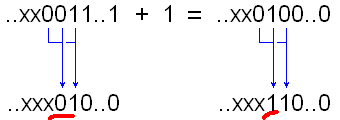 Сур.5. Тақ санға 1, 1-нұсқаға қосыңыз. 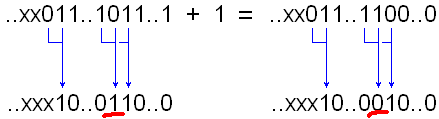 6-сурет. Тақ санды 1-ге, 2-нұсқаға қосыңыз. Бұл жағдайда да, екінші жағдайда да бірінші блоктан кейін битты инверсиялау керек. |
