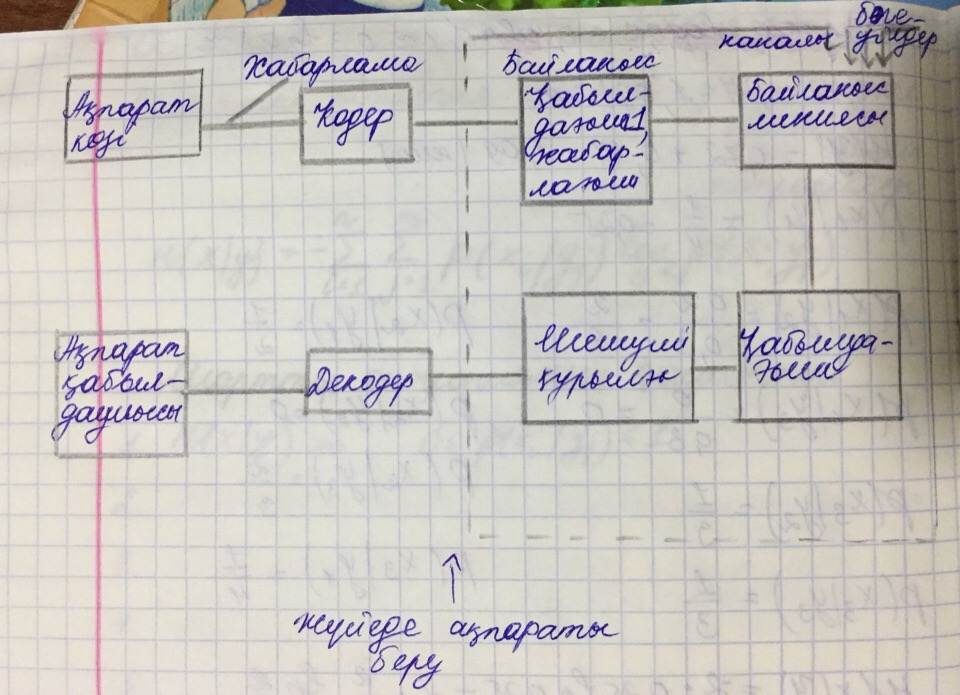
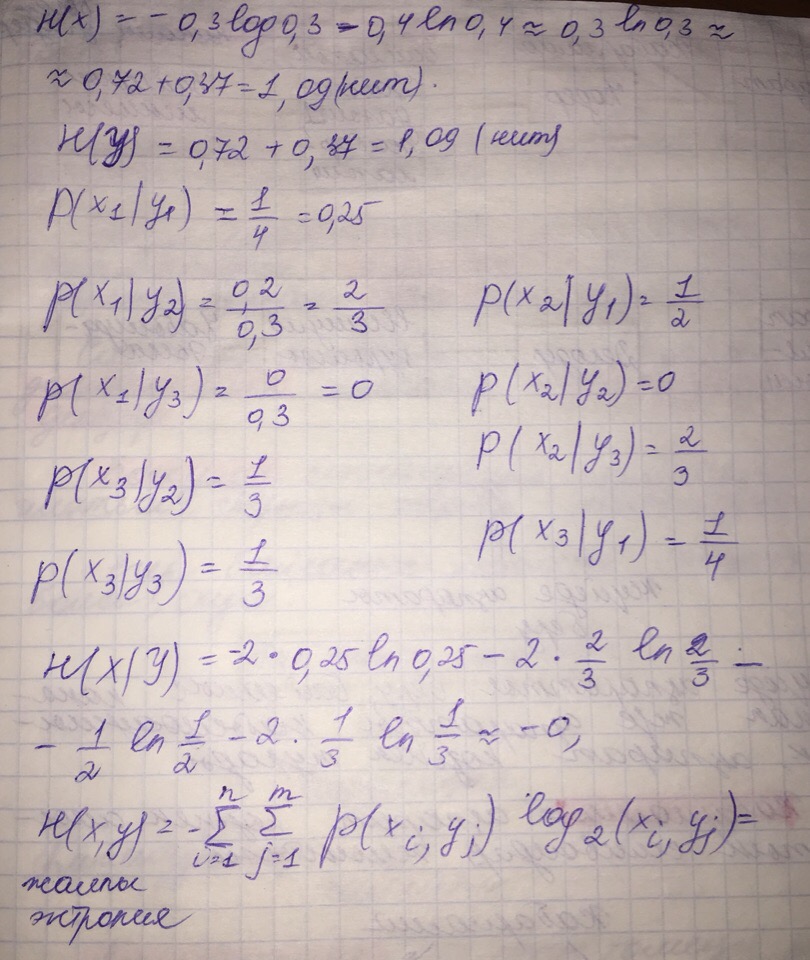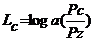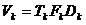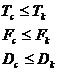ответы основы информоционных систем. ОИС отв. Жйелер теориясыны негізгі элементтерін натылап крсетііз. Жйені асиеттерін атаыз жне р асиетіне сипаттама берііз
 Скачать 1.95 Mb. Скачать 1.95 Mb.
|
|
| Символ | А | Б | В | Г | Д |
| Жиілігі | 15 | 7 | 6 | 6 | 5 |
Бұл үдерісті ағаш құру ретінде көрсетуге болады, оның түбірі — соңғы қадамнан символдарды біріктіру кезінде алынған біріктірілген символдардың ықтималдығы бар символ, оның N0 ұрпақтары — алдыңғы қадамнан алынған символдар және т. б.
Хабарға кіретін әрбір символдар үшін кодты анықтау үшін, біз ағымдағы символға сәйкес келетін ағаш жапырағынан оның тамырына дейін, ағаш бұтақтары бойынша жылжу кезінде биттерді жинай отырып, жолды өту керек (жолдағы бірінші тармақ кіші битке сәйкес келеді). Осылайша алынған биттер тізбегі кері тәртіпте жазылған осы символдың коды болып табылады.
Осы мысал үшін ағаш құру
Бұл таңбалар кестесі үшін Хаффман кодтары келесідей болады.
| Символ | А | Б | В | Г | Д |
| Код | 0 | 100 | 101 | 110 | 111 |
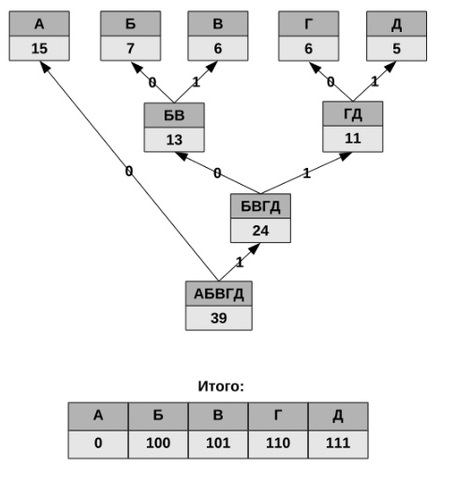
Алынған кодтардың ешқайсысы екіншісінің префиксі болмағандықтан, оларды ағыннан оқылғаннан кейін бірегей түрде декодтауға болады. Сонымен қатар, A хабарламасының ең жиі сипаты аз биттермен кодталады, ал ең сирек D таңбасы ең үлкен болып табылады.
Сонымен қатар, кестеде келтірілген нышандардан тұратын хабарламаның жалпы ұзындығы 87 бит болады (орташа белгі 2,2308 бит). Бірыңғай кодтауды пайдаланған кезде жалпы хабардың ұзындығы 117 бит болады (әр таңбаға 3 бит). Белгіленген жиіліктермен таңбаларды дербес шығаратын көздің энтропиясы - бұл символға 2.1858 биттерді құрайды, яғни осы таңба үшін жасалған Huffman кодының қайталануы, символға және энтропияға арналған биттердің орташа саны арасындағы айырмашылық ретінде түсіндірілген, 0.05 биттерден аз таңба бойынша.
Классикалық Huffman алгоритмінде бірқатар маңызды кемшіліктер бар. Біріншіден, қысылған хабардың мазмұнын қалпына келтіру үшін декодер кодтаушы пайдаланатын жиілік кестесін білуі керек. Демек, қысылған хабарламаның ұзындығы деректерді алға жіберетін жиіліктер кестесінің ұзындығымен көбейтіледі, бұл хабарды қысу үшін бар күш-жігерін жоққа шығарады. Сонымен қатар, нақты кодтауды бастамас бұрын толық жиіліктің статистикасының қажеттілігі хабар арқылы екі өтуді талап етеді: бір хабар үлгісін (жиілік кестесі және H-tree) жасау, екіншісі нақты кодтау үшін. Екіншіден, кодтаудың қайталануы тек кодталған таңбалардың ықтималдығы 2-ші инверсия болып табылған жағдайда ғана жоғалады. Үшіншіден, энтропия 1-ден аспайтын дереккөз үшін (мысалы, екілік дереккөз үшін) Хафман кодын тікелей қолдану мағынасы жоқ.
Сығу коэффиценті:
15+7+6+6+5+11+13+24+39=126
126/8=15,75
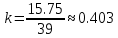
Ақпаратты сығу – деректерді берудің маңызды аспектісі, бұл деректерді жедел түрде беруге мүмкіндік береді. Сығу мақсаты – берілген ақпаратты сақтау және беру үшін қажетті бит санын азайту, бұл ақпаратты үнемді және тиісмді түрде жазуға мүмкіндік береді.
Сығу әдістерін екі үлкен топқа бөлуге болады: қайтарылатын және қайтарылмайтын.
Қайтарылатын алгоритмдер кіріс деректерін ең ықшам кодталатын формаға келтіре отырып, тек кіріс деректерінің берілу тәсілін өзгертеді. Мұндай алгоритмдер үшін кері алгоритм бар, олар сығылған жиымнан алғашқы деректерді қалпына келтіре алады.
Қайтарылатын алгоритмдерді кез-келген типті деректерді сығу үшін қолдануға болады. Ақпаратты жоғалтпай сығылатын файлдар форматтары:
• GIF, TIF, PCX, PNG — графиктік деректер үшін;
• AVI — кезектесетін видео- және дыбыс деректері үшін;
• ZIP, ARJ, RAR, LZH, LH, CAB — деректердің кез-келген типі үшін
Егер сығу кезінде деректер жоғалмайтын болса, онда сығу әдісі қайтарылатын деп аталады
Қайтарылатын әдістердің негізгілері:
1. қаттау әдісі;
2. Хаффман алгоритмі;
3. RLE алгоритмі;
4. Лемпель—Зив алгоритмі.
Хемминг кодының алгоритмін түсіндіріңіз. Хэмминг шекараларын көрсетіңіз. Хэмминг кодына мысал келтіріңіз.
Хэмминг коды - өткен ғасырдың 1940 жылдарында Ричард Хемминг әзірлеген бір қатені түзетуге және қос қателерді түзеуге мүмкіндік беретін блоктық код.
Басқаша айтқанда, бұл қандай да бір ақпараттық хабарламаны белгілі бір жолмен кодтауға және (мысалы, желі бойынша) жібергеннен кейін осы хабарламада қандай да бір қате пайда болғанын анықтауға (мысалы, кедергілерге байланысты) және мүмкіндігінше, осы хабарламаны қалпына келтіруге мүмкіндік беретін алгоритм.
Сондай-ақ, осы алгоритмнің неғұрлым жетілдірілген модификациялары бар екенін атап өткен жөн, олар көптеген қателерді анықтауға мүмкіндік береді (және мүмкін болса түзету).
Бірден айта кету керек, Хэмминг коды екі бөліктен тұрады. Бірінші бөлім белгілі бір орындарда бақылау биттерін (ерекше түрде есептелген) енгізе отырып, бастапқы хабарламаны кодтайды. Екінші бөлім кіріс хабарын алады және бақылау биттерін қайта есептейді (БІРІНШІ БӨЛІМ сияқты алгоритм бойынша). Егер барлық жаңадан есептелген бақылау биттері алынғандармен сәйкес келсе, онда хабарлама қатесіз алынды. Әйтпесе, қате туралы хабарлама шығады және мүмкін болса қате түзетіледі.
Егер кодталатын ақпараттық блоктың ұзындығы m - бит болса. Кодтау үшін пайдаланылатын басқару биттерінің саны k, одан кейін кодталған блок ұзындығы: n = m + k биттерге ие болады. Осы ұзындықтың әр блогы үшін, қателігі бар әр түрлі комбинациялары мүмкін.
Осылайша, берілген әрбір блок үшін блок болуы мүмкін n - блоктары бар бір қате және бір блок қатесіз. Сондықтан, бірден көп қате болмайтын әр түрлі кодталған блоктардың максималды саны болады: 2m(n+1), где n = m+k

Егер m Ұзындығы ақпараттық деректер үшін бақылау биттерінің k санын таңдасаңыз, ұзындығы m+k әр түрлі тізбектердің максималды мүмкін болатын саны бір қатеден аспайтын әр түрлі кодталған ақпараттық блоктардың барынша көп немесе тең болады, онда бір реттік қатені түзетуге кепілдік беретін k бақылау биттерінің көмегімен ақпараттық деректерді кодтаудың осындай әдісі бар екенін дәл айтуға болады.
Демек, бір реттік қатені түзету үшін қажетті бақылау биттерінің ең аз саны теңдіктен анықталады: 2m * (n+1)=2n
n = m + k екенін ескере отырып, біз: k=2k – m – 1
Биттердің саны бүтін сан болуы керек болғандықтан, осы теңдеуді пайдалана отырып есептелген k ең жақын бүтін санға дейін дөңгелектелуі керек.
Мысалы, ұзындығы 7, 4 ақпарат туралы деректер үшін бір реттік қателерді түзетуді қамтамасыз ету үшін бақылау биттары қажет, ал 128 биттердің ұзақтығы үшін 8 бақылау биты қажет.
Қатені түзету үшін қажетті басқару биттерінің ең аз санын анықтау жеткіліксіз. Бұл бақылау биттерін пайдаланып, деректерді тексерудің алгоритмін жасау керек. Ричард Хемминг келесі алгоритмді ұсынды.
Кезектегі реттік сандар екеуі болып табылатын барлық биттер бақылау биті болып табылады. Яғни, егер биттің реттік нөмірі «n» белгісімен белгіленсе, онда басқару биттары үшін теңдік шын болуы керек: n = 2k, мұндағы k - кез келген оң бүтін сан.
Мысалы, ұзындығы 13 бит ұзындықты кодтау үшін, тексерулер келесідей болады: 1, 2, 4 және 8 биттерді құрайды, себебі 20= 1, 21 = 2, 22= 4, 23 = 8
Осылайша, әрбір таңдалған басқару биті биттердің белгілі бір тобын тексереді, яғни. топтың барлық биттерінің екеуі (ол қарапайым нөмірлерге қосымша) тексеру битіне жазылады.
Қандай бақылау биттерін биттерді басқаратындығын анықтау үшін оның дәрежесін 2-дәрежеге қарай бөлшектеу қажет. Осылайша, тоғызыншы бит 1 және 8 биттермен бақыланады, себебі 9 = 20 + 23 = 1 + 8.
Тапсырма. Бұл сөзді Хэмминг кодымен кодтау.
1) 1001 0001 1101 1110 0000 000
ШЕШІМІ. M = 23 ұзындықтағы осы хабарламаны кодтау үшін k = 5 қосымша разряд қажет болады, яғни шығыста N = 28 ұзындықтағы хабарды аламыз (қосымша разрядтардың саны 2K ≥ n+1, n – алынған разрядтардың саны, k – қосымша разрядтардың саны).
Кодталған хабардың түрі болсын
b28 b27 b26 b25 b24 b23 b22 b21 b20 b19 b18 b17 b16 b15 b14 b13 b12 b11 b10 b9 b8 b7 b6 B5 b4 b3 b2 b1,
b1, b2, b4, b8, b16 разрядтары бақылау, ал қалғандары Ақпараттық болады. Ақпараттық разрядтарға рет бойынша бастапқы санның разрядтарын орналастырамыз, яғни.
b3 =1, b5 = 0, b6 = 0, b7=1,
b9=0, b10 =0, b11=0, b12=1,
b13= 1, b14=1, b15=0, b17=1,
b18=1, b19=1, b20=1, b21=0,
b22=0, b23=0, b24=0, b25=0,
b26=0, b27=0, b28=0.
Енді бақылау разрядтарының мәнін табамыз.
Ыңғайлы болу үшін келесі жиындарды енгіземіз:
V1 = 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27... - бірінші разряд 1-ге тең барлық сандар
V2 = 2, 3, 6, 7, 10, 11, 14, 15, 18, 19, 22, 23, 26, 27... - екінші разряд 1-ге тең барлық сандар
V3 = 4, 5, 6, 7, 12, 13, 14, 15, 20, 21, 22, 23, 28... - үшінші разряд 1-ге тең барлық сандар
V4 = 8, 9, 10, 11, 12, 13, 14, 15, 24, 25, 26, 27, 28... - төртінші разряд 1-ге тең барлық сандар,
V5 = 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 ... - бесінші разряд 1-ге тең барлық сандар.
Бұдан әрі + деп 2 Модуль бойынша қосуды түсінеміз.
Сонда b1 = b3+b5+b7+b9+b11+b13+b15+b17+b19+b21+b23+b25+b27 = 1 (барлық разрядтар бірі-V1 қоспағанда, қолданысқа)
B2 = B3+b6+b7+B10+b11+b14+ B15+ b18+ b19+ B22+ b23+ B26+ b27 = 1 (бірінші разрядтан басқа V2 барлық разрядтары)
B4 = B5+b6+b7 +b12+b13+ b14+ b15+ b20 +b21+b22+b23+B28 = 1) (бірінші разрядтан басқа V3 барлық разрядтары)
B8 = B9+B10+b11+B12+b13+b14+B15+b24+b25+B26+b27+B28 = 1), (бірінші разрядтан басқа V4 барлық разрядтары)
b16 = b17+B18+B19+B20+B21+B22+b23+b24+b25+B26+b27+B28 = 0 (бірінші разрядтан басқа V5 барлық разрядтары).
Осылайша, 1111 0011 0001 1100 1111 0000 0000 кодын алды.
1.N=32 ақпараттық комбинация Саны кезінде бір қатені түзететін кодта қанша ақпараттық таңба бар.
2.Жалпы санда түзету кодының артықтығын анықтау
N=256 кодтық комбинациялар.
3.100110 екілік санды ондық жүйеге аудару.
4.Дәлдік ережесі бойынша кодтарды ойластыру:
0101100011
111110001100
0010001010.
5. Хэммминг кодының макетін құру, Хаффман кодының 00101 кодтық комбинациясы үшін түзету разрядтарының мәнін анықтау.
6.Хэмминг кодын пайдалана отырып, 1111 1011 хабарламасында қатені табу
0010 1100 1101 1100 110.
7.Кодтық сөздерді дұрыс тексеру, егер олар Хэмминг кодын пайдаланып жасалған болса. Егер жоқ болса, бастапқы деректерді табу.
-010101100011
-111110001100
-000010001010
8.10011010 тізбегі берілген. Кодпен кодтау Хемминг.
9.H – 01000100, a – 00111101, b – 00111110, r – 01001000. (ескерту. Бастапқы хабарламаны 16 биттен екі блокқа бөлу)
10.Алдыңғы 6 тапсырмадан хабарлама 11-ші қатемен алынды
бит. Қатені табу.


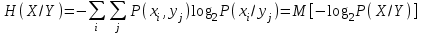 , (1.5)
, (1.5)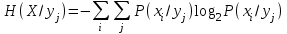 . (1.6)
. (1.6)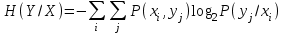 .
.