2020_Бакалавр_Кокишев Д. К. И. Сатпаева Институт промышленной автоматизации и цифровизации Кафедра автоматизации и управления Кокишев Дамир Алтынбекович Исследование
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Анализ динамических свойств системы автоматического управления процессами переработки нефтиИсследование на устойчивость по первому методу Ляпунова разомкнутой и замкнутой системы. Передаточная функция замкнутой системы имеет вид: G(s) = 243.5s + 4382  2 , 2 ,47.55s + 245.3s + 4382 где характеристическое уравнение будет 47.5s2 + 245.3s + 4382 = 0. (10) Корни данного уравнения: s1 = -2.5821 + 9.2515j, s2 = -2.5821 – 9.2515j. Согласно первой теореме Ляпунова, замкнутая система устойчива, так как все действительные части корней характеристического уравнения меньше нуля. Передаточная функция разомкнутой системы записывается из формулы 6: T(s) = 243.5s + 4382  2 , 2 ,47.55s + 490.6s + 8764 где характеристическое уравнение будет 47.5s2 + 490.6s + 8764 = 0. (11) Решив уравнение, получится корни: s1 = -5.1642 + 12.5632j, s2 = -5.1642 – 12.5632j. Согласно первой теореме Ляпунова, разомкнутая система устойчива, так как все действительные части корней характеристического уравнения отрицательные. Исследование разомкнутой дистанционной следящей системы на устойчивость по критерию устойчивости Гурвица. В качестве исходных данных для исследования разомкнутой системы на устойчивость по критерию Гурвица используется её характеристическое уравнение (11). Откуда следует, что параметры равны [9]. a0 = 47.5, a1 = 490.6, a2 = 8764. Затем по данным параметрам была построена матрица Гурвица: | , |490.5 0 47.5 8764 Определители главных миноров равны: Δ1 = 490.5, Δ2 = 4298742. В соответствии с критерием Гурвица, разомкнутая система является устойчивой, так как все определители главных диагональных миноров больше нуля. Исследование замкнутой дистанционной следящей системы на устойчивость по критерию устойчивости Гурвица. В качестве исходных данных для исследования замкнутой системы на устойчивость по критерию Гурвица используется её характеристическое уравнение (10). Откуда следует, что параметры равны: a0 = 47.5, a1 = 243.5, a2 = 4382. Затем по данным параметрам была построена матрица Гурвица: |. |243.5 0 47.5 4382 Определители главных миноров равны: Δ1 = 243.5, Δ2 = 1067017. В соответствии с критерием Гурвица, замкнутая система является устойчивой, так как все определители главных диагональных миноров больше нуля. Исследование замкнутой системы на предельный критерий усиления и нахождения области значения коэффициента усиления для устойчивости системы. Для исследования замкнутой системы на предельный критерий усиления необходимо использовать передаточную функцию разомкнутой системы [10]:  T(s) = 243.5s+4382 . T(s) = 243.5s+4382 .47.55s2+490.6s+8764 Далее необходимо разложить знаменатель на множители:  T(s) = 235.5s+4382 . T(s) = 235.5s+4382 .(s+10.37)(47.55s+665) Затем нужно найти предельный коэффициент усиления, а после заменить его на k.  T(s) = 81.3(0.18s+1) . T(s) = 81.3(0.18s+1) .(s+10.37)(47.55s+665)  T(s) = k(0.18s+1) T(s) = k(0.18s+1). (12) (s+10.37)(47.55s+665) Далее из преедаточной функции разомкнутой системы (12) получим передаточную функцию замкнутой системы с предельным коэффициентом усиления k:  T(s) = k(0.18s+1) T(s) = k(0.18s+1)(s+10.37)(47.55s+665)+k(0.18s+1) . (13) Для того, чтобы найти области значения коэффициента усиления для устойчивости системы необходимо рассмотреть характеристическое уравнение (выражение 13) и затем построить матрицу Гурвица: (s + 10.37)(47.55s + 665) + k(0.18s + 1) = 0, 47.55s2 + (712.31 + 0.18k)s + 689.3 + k = 0, |. |712.31 + 0.18k 0 47.55 689.3 + k Далее найдем определитель матрицы: Δ = 0.18k2 + 208.31k + 301 > 0. (14) Решим неравенство 14: k1 > 0, k2ϵ(−32.8; 28.31), kϵ(0; 28.31). Была найдена область значений коэффициента усиления для устойчивости, а также найден предельный коэффициент усиления замкнутой системы kпр1 = 0, kпр2 = 28.31.
Прямые оценки качества переходного процесса замкнутой системы автоматического управления процессами переработки нефти. Исходными данными для прямой оценки качества переходного процесса является замкнутая система. Используя Liner Analysis Point обозначаются входные и выходные точки для оценки качества системы. Через контекстное меню Analysis – Control Design – Liner Analys открывается окно для прямой оценки, которое показано на рисунке 2.11. После получения переходного процесса объекта управления, необходимо отобразить основные данные оценки качества нажатием на правую клавишу мыши и выбрав в контекстном меню пункты Characteristics – Peak Response; Rise Time; Settling Time; Steady State. 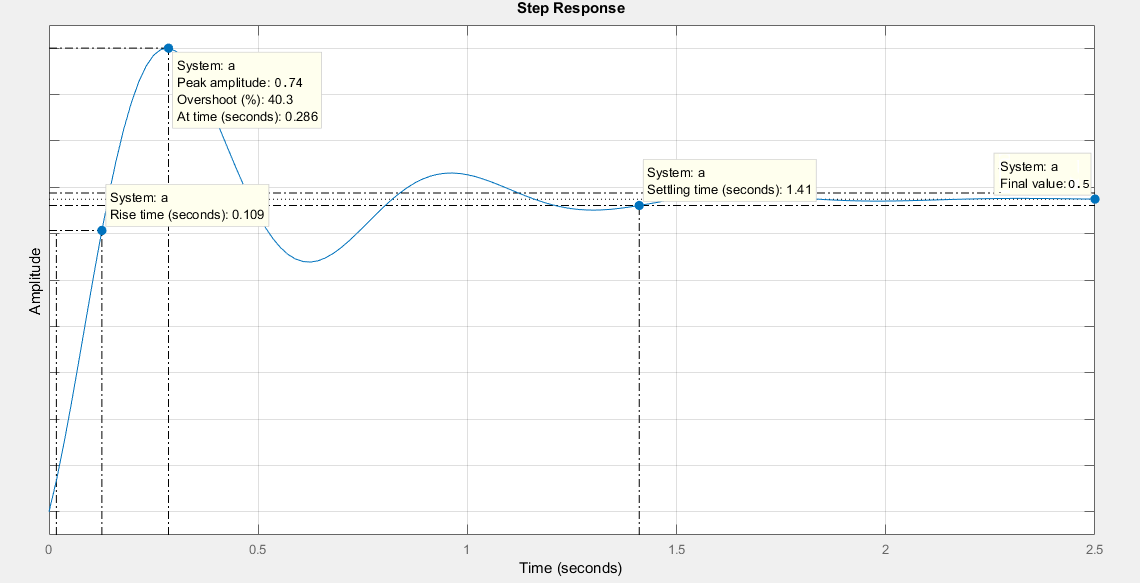 Рисунок 2.11 – Переходной процесс замкнутой системы Из графика можно получить следующие данные касательно прямой оценки: Перерегулирование: Pov = 40,3%, время достижения первого максимума: T1max = 0,286 секунд; Время регулирования: Tset = 1,41 секунд; Установившийся значение: yss = 0.5; Время нарастания: Tset = 0.109 секунд. По этим данным можно получить полную прямые оценки качества замкнутой системы: Время регулирования: Tset = 1,41; Перерегулирование: Pov = 40,3%; Количество колебаний: n = 2; – Колебательность: µ = 0.08/0.40 * 100% = 20%; Частота колебаний: w = 2pi/T = 9.2; Время достижения первого максимума: T1max = 0,286; Время нарастания: Tr = 0.109; Установившийся ошибка: ess = 0.5 Декремент затухания: χ = 6. Косвенные оценки качества переходного процесса замкнутой системы автоматического управления процессами переработки нефти. Исходными данными для косвенной оценки качества переходного процесса является замкнутая система. Также как с прямыми оценками через LTI viewer создаются входные и выходные точки и добавляются в окно LTI analysis. 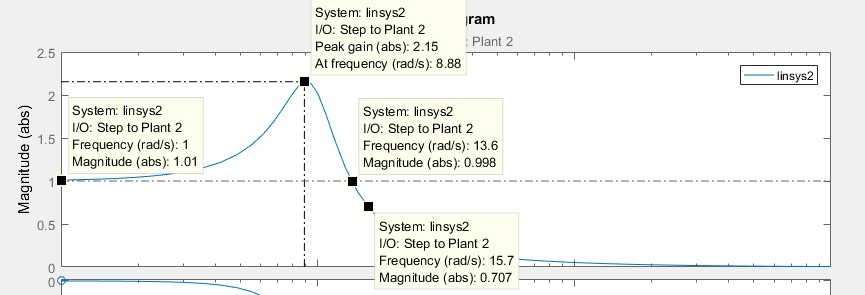 Рисунок 2.12 – Косвенные оценки качества замкнутой системы Из графика можно получить следующие данные, по косвенной оценке, качества: Частота среза: 13.8 Полоса пропускания: [0; 15.7]; Резонансная частота: wr = 8.88 при Amax = 2.15 По этим данным можно получить полную косвенные оценки качества замкнутой системы: Резонансная частота: wr = 8.88 Полоса пропускания системы: [0; 15.7]; Колебательность системы: µ = 2.15/1 = 2.15; Частота среза: 13.8; Далее необходимо получить косвенные оценки качества замкнутой системы автоматического управления процессами переработки нефти на основе корневых методов. Используя LTI viewer, можно получить карту нулей и полюсов, как показано на рисунке 2.13. 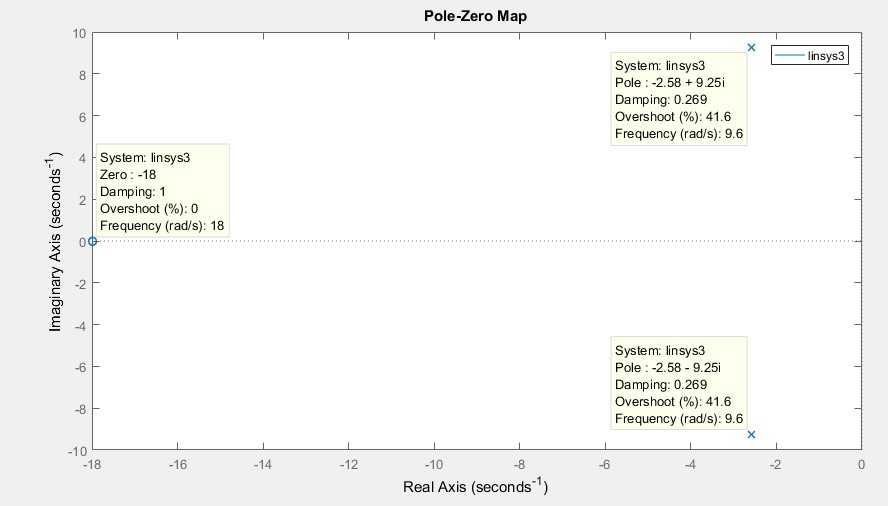 Рисунок 2.13 – Полюса и ноль на комплексной плоскости По графику можно получить следующие данные: s1, s2 = -2.58 ± j9.25, s3 = -18. Получим следующие оценки качества замкнутой системы автоматического управления процессами переработки нефти: Время регулирования: Tset = 4  |σ| |σ|= 4  2.58 2.58= 1.55 c. Перерегулирование: ε∗pi − Pоv = e √1−ε2 ∗ 100% = e−877 ∗ 100% = 41%. Максимальное значение, ymax: ymax = yf (1 + Pоv) = 1.4. 100 Степень колебательности:   μ = β = 9.25 = 3.58%. μ = β = 9.25 = 3.58%.Частота колебаний: α 2.58   w = ωn√(1 − Ɛ2) = 9.6√(1 − 0.2692) = 9.2 c−1. Время достижения первого максимума: T1max = π  ωn√(1−Ɛ2) ωn√(1−Ɛ2)= 3.14  9.6√(1−0.2692) 9.6√(1−0.2692)= 0.34 c. Быстродействие и степень устойчивости: η = |σmin| = 2.58. Полученные данные косвенных оценок вставляется в таблицу 2.6 и сравнивается с прямыми оценками качества. Таблица 2.6 – Оценки качества замкнутой системы
Вывод: Перерегулирование составляет 48.3%, что не соответствует желаемому значению 30%, колебательность составляет 16%, что также не соответствует желаемым требованиям. В соответствии с этим необходимо синтезировать типовой регулятор. С целью улучшения перерегулирования введем интегрирующую составляющую в регулятор, с целью уменьшения колебательности введем дифференцирующую составляющую, с целью уменьшения времени регулирования введем пропорциональную составляющую. В качестве критерия качества выберем квадратично- интегральный критерий качества, так как он дает общую оценку времени регулирования и степень отклонения заданной величины от желаемого значения в переходном процессе.
Постановка задач: для математической модели объекта управления (6) необходимо синтезировать ПИД-регулятор: u(t) = k e(t) + 1 ∫ e(t)dt + T  de(t),  p Ti d d(t) f(x): используя алгоритм роя частиц, где рассматривается целевая функция 0 f(x) = ∫∞|e(t)|dt → min, которая непрерывно ограничена областью ub и lb и найти приближенное минимальное значение функции f*(x)min или координату x*min, в которой это значение достигается с заданной допустимой vMax и vMin. fmin = minf(x) = f(xmin), (15) f ∗ = f(x∗ ) ≤ fmin + ε, (16) min min где ε – допустимая скорость, в нашем случае vMax, vMin. Трехфазные сепараторы используются для разделения скважинной сырой нефти на три части: воду, нефть и газ. Для обеспечения оптимальной работы трехфазного сепаратора должна быть создана соответствующая система управления. Текущая методика настройки ПИД не обеспечивает оптимальную реакцию системы сепаратора. Реакция на превышение скорости, смещение, установившаяся ошибка и нестабильность системы-вот некоторые из проблем, с которыми приходится сталкиваться. Кроме того, используемый в настоящее время метод основан исключительно на пробах и ошибках, что отнимает много времени. [11] Существует возможность для совершенствования существующей методики настройки ПИД. Для улучшения отклика системы трехфазного сепаратора вводится метод ПИД-настройки искусственного интеллекта (AI), называемый оптимизацией роя частиц (PSO) [12]. Алгоритм PSO имитирует поведение стаи птиц и стай рыб, стремящихся к своему глобальному наилучшему положению [13]. В нашем случае глобальная наилучшая позиция заменяется оптимизированными параметрами настройки ПИД для сепаратора. Алгоритм PSO был использован в нескольких других приложениях, таких как бесщеточный двигатель постоянного тока и в системе управления шариком и Лучом. Это оказалось эффективным методом настройки. Настройка трехфазного сепаратора с помощью PSO может оказаться эффективным решением для нефтегазовой промышленности. Для настройки регулятора уровня трехфазного сепаратора был введен метод искусственного интеллекта (ИИ), известный как оптимизация роя частиц (PSO). 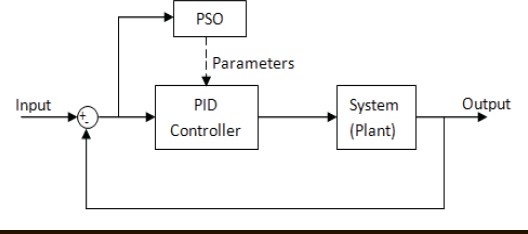 Рисунок 2.14 – Реализация PSO в ПИД-регуляторе Рассматривая рой с частицами P, существует вектор положения 𝑋𝑡 = 𝑖 𝑖 (𝑥𝑖1𝑥𝑖2𝑥𝑖3 … 𝑥𝑖4)𝑇 и вектор скорости 𝑉𝑡 = (𝑣𝑖1𝑣𝑖2𝑣𝑖3 … 𝑣𝑖𝑛)𝑇 на t-й итерации для каждой из составляющих ее i-частиц. Эти векторы обновляются через размерность j в соответствии со следующими уравнениями: Vt+1 = wVt + c1rt (pbestij − Xt ) + c2rt (gbestj − Xt ), (17) ij ij 1 ij 2 ij Xt+1 = Xt + Vt+1. (18) ij ij ij Уравнение 17 изменяет вектор скорости при каждой итерации. Уравнение 18 обновляет положение частицы. Этот параметр важен для балансировки глобального поиска, также известного как разведка (когда установлены более высокие значения), и локального поиска, известного как эксплуатация (когда установлены более низкие значения). Первое слагаемое уравнения обновления скорости, формула 17, является произведением между параметром w и предыдущей скоростью частицы, поэтому он обозначает предыдущее движение частицы в текущую. Следовательно, например, если w = 1, то движение частицы полностью зависит от ее предыдущего движения, поэтому частица может продолжать двигаться в том же направлении. С другой стороны, если 0 ≤ w < 1, то такое влияние уменьшается, а это значит, что частица скорее переходит в другие области области поиска. Таким образом, по мере уменьшения параметра инерционного веса рой может исследовать больше областей в области поиска, а это означает, что шансы найти глобальный оптимум могут увеличиться. Однако существует цена при использовании более низких значений w, то есть моделирование оказывается более трудоемким. Второе слагаемое уравнения вычисляется с помощью разности между собственным лучшим положением частицы, в этом случае pbestij, и ее текущим положением Xtij. Концепция, лежащая в основе этого слагаемого, заключается в том, что по мере удаления частицы от положения pbestij разница (pbestij−Xtij) должна увеличиваться; следовательно, это слагаемое увеличивается, привлекая частицу к ее лучшему собственному положению. Параметр С1, существующий как произведение в этом выражении, является положительной константой, и он взвешивает важность собственного предыдущего опыта частицы. Другим параметром, составляющим произведение второго члена, является r1, и это случайный параметр с диапазоном [0,1]. Этот случайный параметр играет важную роль, так как позволяет избежать преждевременных конвергенций, увеличивая наиболее вероятные глобальные оптимумы. Наконец, третье слагаемое – это социальное обучение. Благодаря этому все частицы в рое способны делиться информацией о наилучшей достигнутой точке независимо от того, какая частица ее нашла, например gbestj. Его вид точно такой же, как и второе слагаемое, тот, что касается индивидуального обучения. Таким образом, разность (gbestj−Xtij) действует как притяжение частиц к лучшей точке, пока не будет найдена на некоторой t-й итерации. Точно так же с2 - это параметр социального обучения, и он взвешивает важность глобального обучения Роя и r2 играет точно такую же роль, как и r1. На рисунке 2.15 показана логика роя частиц для оптимизации ПИД- регулятора: 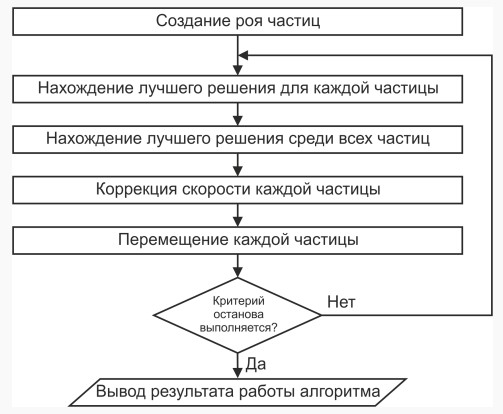 Рисунок 2.15 – Логика роя частиц В начале в некой плоскости (область поиска) случайно создается рой частиц, где у каждой частицы свой вектор скорости. В каждой точке координат, где была частица высчитывается значение целевой функции. Каждая частица запоминаем самое лучшее значение и его координаты. После каждой итерации частицы корректируют свою скорость относительно лучшему значению целевой функции, чтобы быть как можно ближе к нему уменьшая расстояние, то есть ошибку также быть ближе к глобальному лучшему значению. Через некоторое время частицы должны собраться в одном месте и найти самое подходящее значение с допустимой погрешностью ε [14]. Логика алгоритма для данной работы показана на рисунке 2.16. 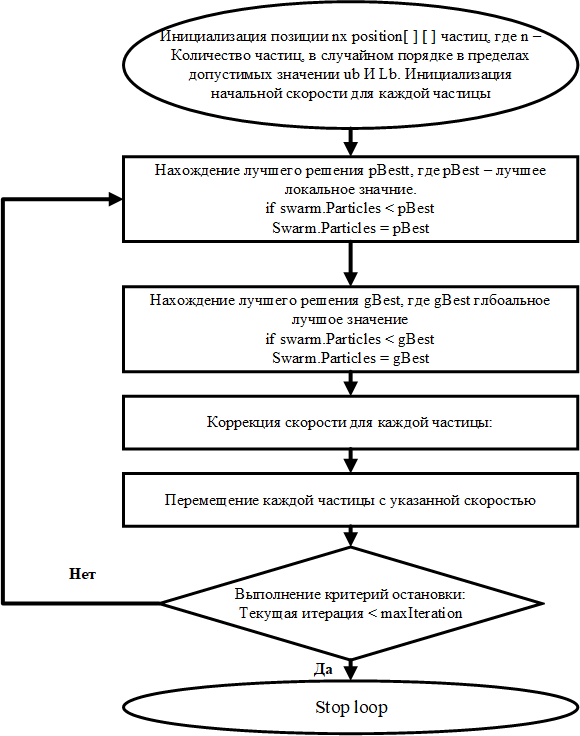 Рисунок 2.16 – Алгоритм PSO для объекта управления На основе этой логики и будет построен алгоритм для оптимизации ПИД- регулятора. Сначала необходимо объявить переменные начальной популяции роя, максимальное количество роя (птиц), инерция и скорость движения роя, рисунок 2.17 [15].  Рисунок 2.17 – Дефолтная функция объявления переменных Необходимо инициализировать начальные позиции роя, их скорость и лучшую позицию, рисунок 2.18.  Рисунок 2.18 – Инициализация начальных условий Создается начальная популяция, рисунок 2.19.  Рисунок 2.20 – Вычисление значения частицы Далее необходимо найти локальное лучшее значение частицы pBest, если текущее значение лучше pBest, нужно обновить их, рисунок 2.21.  Рисунок 2.21 – Нахождение и обновление pBest Согласно нарисованному на рисунке 2.16 алгоритму необходимо найти глобальное лучшее значение частицы gBest и обновить его, рисунок 2.22. 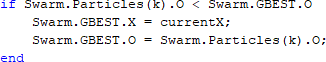 Рисунок 2.22 – Нахождение и обновление gBest Далее нужно изменить инерционность исходя из количества итерации, показан на рисунке 2.23. Рисунок 2.23 – Изменение инерционности При приближении к лучшему значению необходимо обновить скорость роя, рисунок 2.24. Рисунок 2.24 – Обновление скорости После изменения скорости нужно проверить скорость согласно ограничениям vMax и vMin, рисунок 2.25 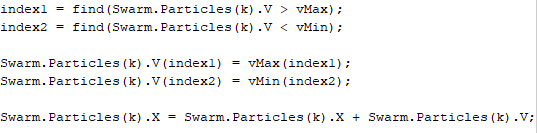 Рисунок 2.25 – Проверка скорости Далее нужно проверить позиции согласно ограничениям ub и lb, рисунок 2.26.  Рисунок 2.26 – Проверка позиции Интегральный критерий качества относительно абсолютного значения от ошибки пишется в другой файл для удобства, рисунок 2.27. 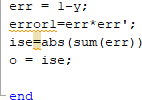 Рисунок 2.27 – Интегральный критерий качества При успешном написании кода в конце командной строке выйдут параметры ПИД-регулятора, как показано на рисунке 2.28. 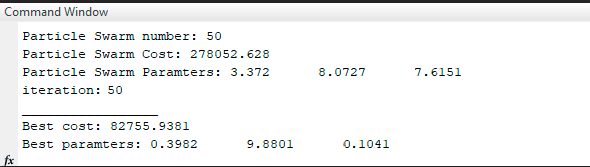 Рисунок 2.28 – Результат выполнения алгоритма роя частиц (PSO) В итоге получены параметры Kp = 0.3982; Ki = 9.8801; Kd = 0.1041 для ПИД-регулятора:  u(t) = 0.3982 ∙ e(t) + 1 u(t) = 0.3982 ∙ e(t) + 19.8801 ∫ e(t)dt + 0.1041 de(t). (19)  d(t) d(t)Далее эти коэффициенты вводятся в настройки ПИД-регулятора и сравнивается с обычной системой без регулятора в среде MATLAB. На рисунке 2.29 представлена схема моделирования в среде Simulink математической модели трехфазного сепаратора с ПИД-регулятором PSO (19), ПИД регулятором Autotune и без ПИД-регулятора. 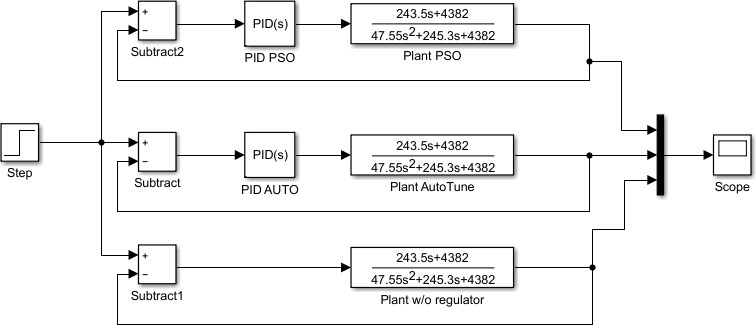 Рисунок 2.29 – Структурная схема для сравнения переходных процессов с регулятором и без регулятора На рисунке 2.30 показан график переходного процесса системы с ПИД- регулятором PSO показана черным цветом, ПИД-регулятором AutoTune показана красным цветом и системы без ПИД-регулятора, показана синим цветом. 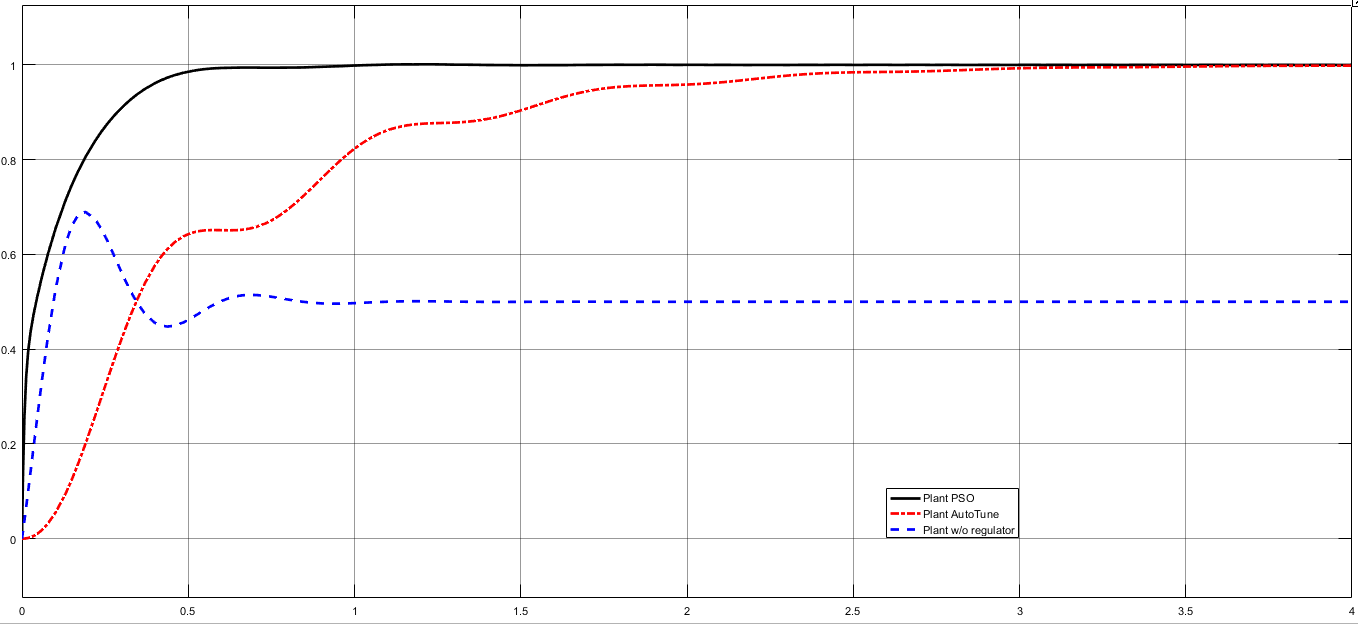 Рисунок 2.30 – График переходных процессов Как видно из рисунка, график системы с ПИД-регулятор приходит к установившемуся значению, сводя ошибку к нулю, улучшилось быстродействие системы. Для более наглядного сравнения системы с ПИД- регулятором на основе алгоритма роя частиц, с ПИД-регулятором AutoTune и без ПИД-регулятора составим таблицу 2.7. Таблица 2.7 – Оценки качества замкнутой системы с регуляторами
Исходя из данных в таблице, можно сделать вывод, что система с ПИД- регулятором на основе алгоритма роя частиц обладает лучшим временем регулирования – 1с, отсутствие перерегулирования, система монотонна, установившаяся ошибка равна 0. Система с ПИД-регулятором AutoTune обладает довольно таки большим временем регулирования по сравнению с системами без ПИД-регулятора и С ПИД-регулятором PSO и равна 3.6с. Также отсутствует перерегулирование, но при этом имеется 3 колебания. Установившаяся ошибка равна нулю. Система без ПИД-регулятора обладает перерегулированием 40.3%, что превосходит допустимое значение в 30%, также установившаяся ошибка равна 0.5, что и является главной проблемой, задача которой была решена с использованием ПИД-регулятора на основе метода роя частиц. |
