2020_Бакалавр_Кокишев Д. К. И. Сатпаева Институт промышленной автоматизации и цифровизации Кафедра автоматизации и управления Кокишев Дамир Алтынбекович Исследование

• Название: К. И. Сатпаева Институт промышленной автоматизации и цифровизации Кафедра автоматизации и управления Кокишев Дамир Алтынбекович Исследование
• Дата: 21.08.2022
• Размер: 0.83 Mb.
• Имя файла: 2020_Бакалавр_Кокишев Д.docx
• Тип: Исследование; #649704
• страница: 6 из 8

Расчетная часть

1. 
   Разработка схем и моделирование процессов переработки нефти на Павлодарском нефтехимическом заводе
   

Некоторые эксплуатационные данные по расходам воды и нефти показаны на рисунке 2.1. Здесь наблюдаются явные колебания скорости оттока воды.

Уровни воды и нефти внутри сепаратора показаны на рисунке 2.2. Можно наблюдать, что колебания уровня воды находятся в гораздо меньшем масштабе (процентах) по сравнению с колебаниями скорости оттока воды, как показано на рисунке 2.1, особенно после первых 1000 сек. Некоторые проблемы с перенапряжением также можно наблюдать, анализируя эти данные.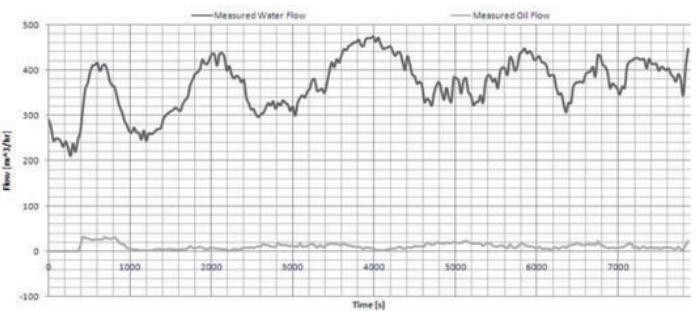


Рисунок 2.1 – Измеренные скорости оттока воды и нефти за определенный промежуток времени
Например, в течение периода 3900 сек. до 4100 сек., из рисунка 2.2, уровень воды немного ниже среднего, в то время как из рисунка 2.2 очевидно, что скорость оттока воды увеличивается.

Между тем, скорость оттока нефти довольно низка, и уровень нефти в этот период снижается. Все эти наблюдения позволяют сделать вывод о том, что в этот период происходили большие всплески воды или газа [8].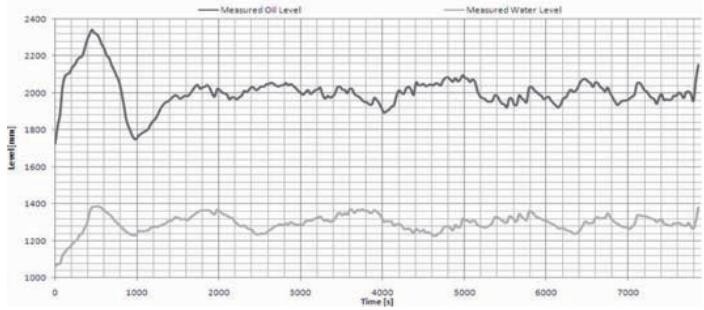


Рисунок 2.2 – Измеренные уровни воды и нефти в течение определенного интервала времени
Системные параметры и переменные, используемые ниже, перечислены в таблице 2.1
Таблица 2.1 - Системные переменные и параметры

Обозначение	Описание	Единица измерения
h(t)	Уровень воды внутри сепаратора	m
Qin(t)	скорость притока воды	m3/h
Qout(t)	скорость оттока воды	m3/h
r	радиус поперечного сечения сепаратора	m
L	длина водного участка	m
h0(t)	уровень нефти внутри сепаратора	m
Pg(t)	давление газа внутри сепаратора	Pa
Cv	Коэффициент выпуска выпускного клапана	-
u(t)	процент открытости клапана	-
ρw	плотность воды при рабочей температуре.	kg/m2
ρo	плотность масла при рабочей температуре.	kg/m2
Pw	давление клапана вниз по потоку	Pa
Umax	максимальная площадь открытия регулирующего клапана	m2
ΔPout	перепад давления над регулирующим клапаном	Pa

В соответствии с геометрией сепаратора, объем воды внутри сепаратора является функцией уровня воды h и имеет определенное соотношение как:

V⁽h⁾ = (r²cos⁻¹ (^r−h) − ⁽r − h⁾√2rh − h²L. (1)

r
Поскольку для нормальной работы требуется уровень воды между уровнем тревоги высокого уровня (LAH) и уровнем сигнала тревоги низкого уровня (LAL), таким образом, соотношение (1) может быть упрощено как линейная зависимость в течение этого интервала, то есть V(h) = ALh(t) где A

≈ πr2.

Динамика объема воды внутри сепаратора соответствует принципу баланса масс, т. е.:

dV(t) _{≈ AL} dh⁽t⁾ _{= Q}



⁽t⁾ − Q

⁽t⁾. (2)

dt dt ⁱⁿ

out

Согласно теории динамики потока, расход воды через клапан LCV- 340018 можно определить как:

^Qout

= C_v

^f(u)√^{∆Pout, (3)}

ρw

где f(u) представляет характеристики клапана зоны открытости, относящиеся к проценту открытости u. Для этого конкретного линейного клапана LCV-340018 линейное соотношение хорошо соблюдается. Таким образом, существует f(u) = uUmax. Перепад давления на клапане, обозначенный как P_out, можно оценить как:
ΔP_out⁽t⁾ = P_g⁽t⁾ + ρ₀gh₀⁽t⁾ + ρ_wgh⁽t⁾ − P_w⁽t⁾. (4)
Коэффициент C_v клапана в (3) оценивается с использованием метода наименьших квадратов на основе записанных данных о расходе воды, уровнях воды и масла внутри сепаратора, давлении газа внутри сепаратора и давлении воды на выходе. При условии, что плотность воды постоянна, значение Cv будет решением:

min_cv

^∑_i |Q
out

⁽i⁾ − C_v

u⁽i⁾U
max

_√ΔP_out⁽i⁾ _|2.

ρw

Проверка полученной модели системы показана на рисунке 2.3. В общем случае погрешность предсказания ограничена в пределах 10%. Валидация данной модели находится в пределах допустимых значений.

В предположении, что давление газа, давление ниже по потоку водяного клапана и уровень масла внутри сепаратора являются постоянными или их отклонения от средних значений игнорируются, нелинейная модель системы линеаризуется при нормальных условиях эксплуатации.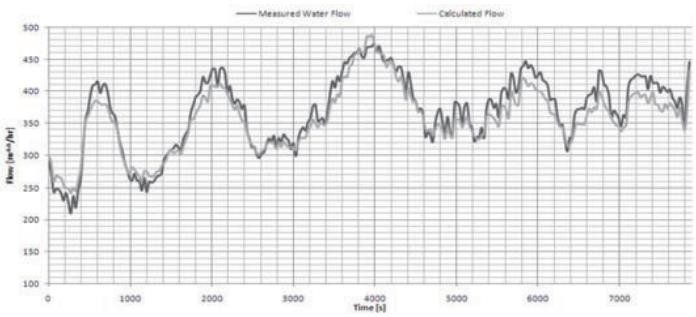

Рисунок 2.3 – Валидация модели: измеренные и прогнозируемые

скорости оттока
В предположении, что давление газа, давление ниже по потоку водяного клапана и уровень масла внутри сепаратора являются постоянными или их отклонения от средних значений игнорируются, нелинейная модель системы линеаризуется при нормальных условиях эксплуатации. Вставляя конкретные параметры системы, линеаризованная модель приводит к форме:

in
47.55 ^dΔh(t) = Q

dt

⁽t⁾ − 1.81Δh⁽t⁾ − 10.82Δu⁽t⁾,

где Δh(t) (Δu(t)) представляет отклонения уровня воды (положение клапана) до равновесия. Таким образом, передаточная функция, представляющие отношения от неизвестного возмущения Q_in(t) и управляющего входа u (t) к выходу h (t), соответственно, будет выглядеть вот так:

_{G(s) =} 243.5s+4382

47.55s²+245.3s+4382

. (5)

На рисунке 2.4 представлена структурная схема математической модели в Simulink.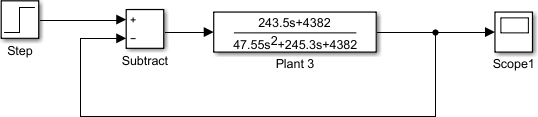




Рисунок 2.4 – Структурная схема в матлабе

Результаты моделирования представлен на рисунке 2.5.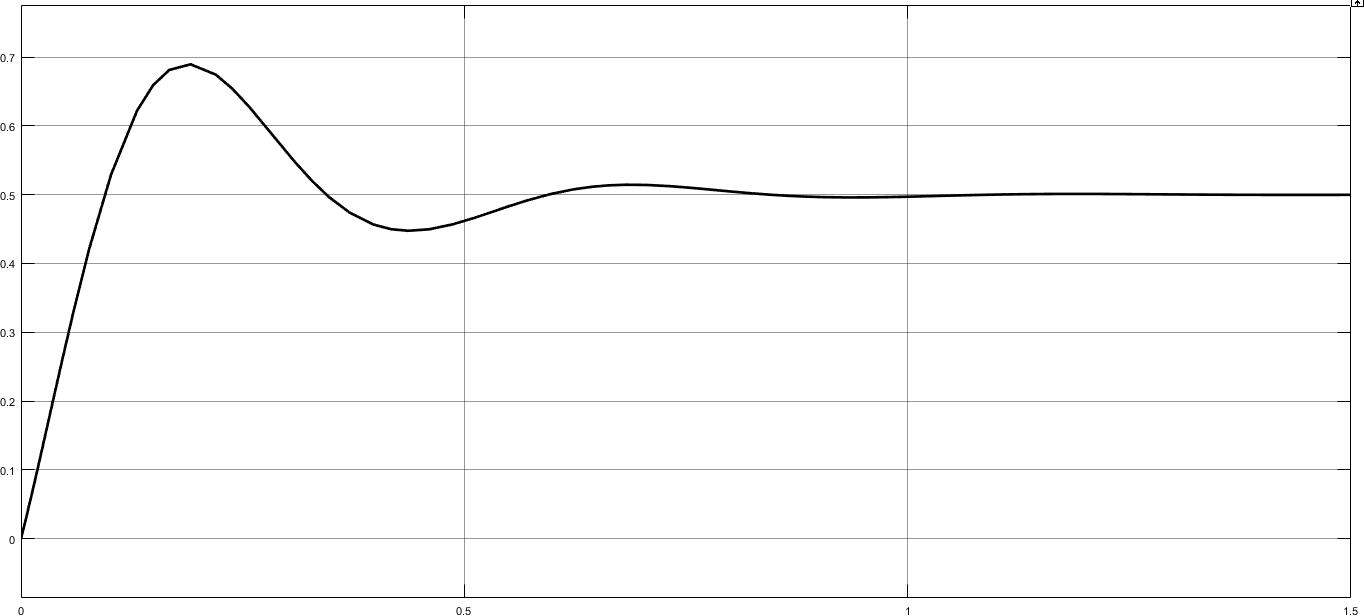



Рисунок 2.5 – Результат моделирования структурной схемы
Как видно из рисунка, система устойчива, но не приходит к желаемому значению (1) и имеется перерегулирование. С целью улучшения динамики системы синтезируем типовой регулятор.

2. Получение результатов моделирования системы автоматического управления процессами переработки нефти

Построение АФЧХ разомкнутой системы. Для построения АФЧХ сначала необходимо определить мнимые и действительные части характеристического уравнения разомкнутой системы:

_{T(s) =} 243.5s+4382

47.55s²+490.6s+8764

. (6)

Далее нужно использовать постановку с оператора Лапласа s в комплексную переменную jw:
_{T(jw) =} j243.5w+4382 _.

j²47.55w²+j490.6w+8764
Для упрощения этого выражения необходимо избавится от мнимой части в знаменателе:
_{T(jw) =} −j11578.425w³−88903w²−j157752w+38403848_.

76807696−592768.04w²+2261.0025w⁴

Отделяем действительную и мнимую часть по формуле:
T⁽jw⁾ = Re⁽w⁾ + jIm⁽w⁾. (7)

_{T(jw) =} −88903w²[phone]

76807696−592768w²+2261w⁴

_{− j} 11578.425w³+157752w _.

76807696−592768w²+2261w⁴

Извлекаем из выражения действительную и мнимую часть:

_{Re(w) =} −88903w²[phone]

76807696−592768.04w²+2261.0025w⁴
_{Im(w) = −} 11578.425w³+157752w

, (8)
. (9)

76807696−592768.04w²+2261.0025w⁴
Подбирая различные частоты, заполняется таблица 2.2 Таблица 2.2 – Таблица значений реальной и мнимой части

w	0	5	10	15	∞
Re(w)	0.5	0.57	0.735	0.321	0
Im(w)	∞	-0.0239	-0.296	-0.679	0

Используя данные в таблице 2.2, построим график АФЧХ разомкнутой системы, который представлен на рисунке 2.6.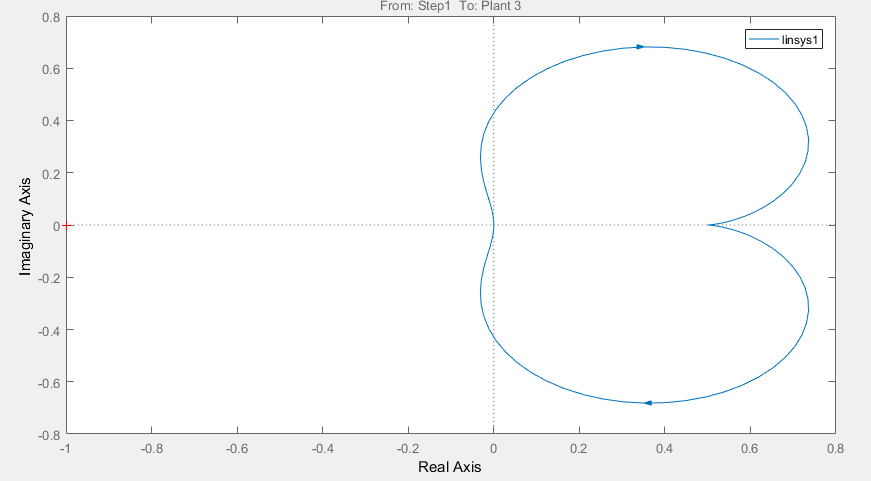



Рисунок 2.6 – График АФЧХ разомкнутой САУ

Построение АЧХ и ФЧХ разомкнутой системы. Для построения амплитудно-частотной характеристики используется нижеследующая формула




A⁽w⁾ = ^√Re²⁽w⁾ + Im²⁽w⁾.
Подставляем уравнения из 8 и 9 формулы и составляем таблицу значений АЧХ.
Таблица 2.3 – Таблица значений АЧХ

w	0	10	100	∞
A(w)	∞	0.794	0.05	0

Используя данные в таблице 2.3, построим график АЧХ разомкнутой системы, который представлен на рисунке 2.7.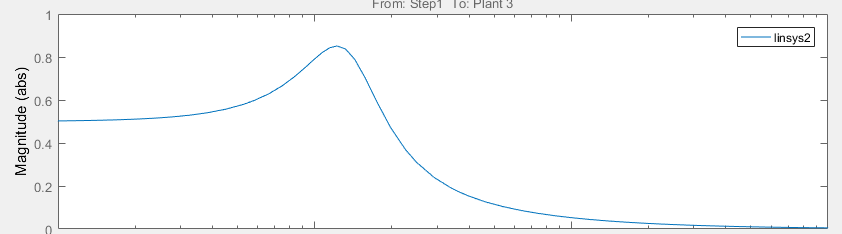



Рисунок 2.7 – График АЧХ разомкнутой системы
Для построения же фаза-частотной характеристики используется следующая формула:

φ⁽w⁾ = atan

Im(w) Re(w)^.

Также как в предыдущих случаях давая значения 𝑤𝜖[0; +∞], составляется таблица 2.4 значений ФЧХ.
Таблица 2.4 – Таблица значений ФЧХ

w	0	1	10	100	1000	∞
𝜑 (w)	0	-0.0447	-24.1	-94.2	-90	-90

Используя данные в таблице 2.4, построим график ФЧХ разомкнутой системы, который представлен на рисунке 2.8.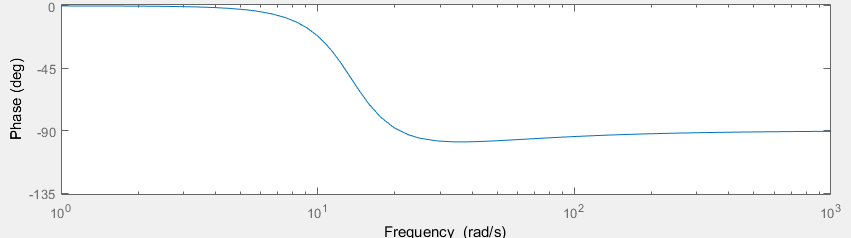




Рисунок 2.8 – График ФЧХ разомкнутой системы Построение ЛАЧХ и ЛФЧХ разомкнутой системы. Для построения

используется следующая формула:
L⁽w⁾ = 20 lg(A⁽w⁾).
Подставляя значения 𝑤𝜖[0; +∞], заполняется нижняя таблица Таблица 2.4 – Таблица значений ЛАЧХ разомкнутой системы

w	0	1	10	100	1000
𝜑 (w)	0	-5.97	-2.01	-25.6	-45

Используя данные в таблице 2.4, построим график ЛАЧХ разомкнутой системы, который представлен на рисунке 2.9.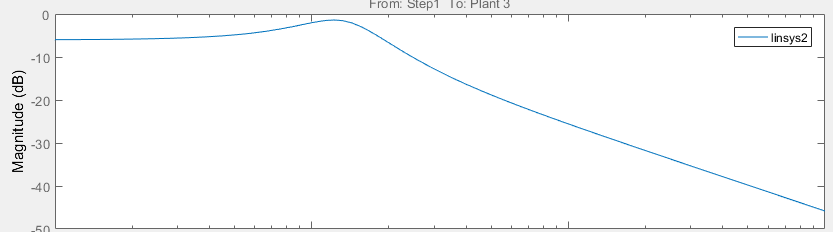



Рисунок 2.9 – График ЛАЧХ разомкнутой системы Для ЛФЧХ используется следующая формула:

φ⁽w⁾ = atan

Im(w)

Re(w)^.

По таблице 2.5 строится график, как показано на рисунке 2.11. Таблица 2.5 – Таблица значений ЛФЧХ разомкнутой системы

w	0	1	10	100	1000	∞
𝜑 (w)	0	-0.0461	-22.1	-94.2	-90	-90

Используя данные в таблице 2.5, построим график ЛФЧХ разомкнутой системы, который представлен на рисунке 2.10.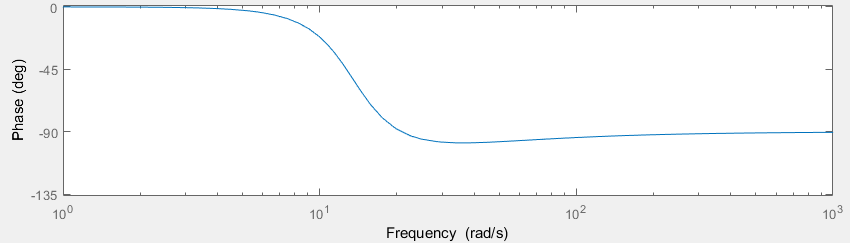



Рисунок 2.10 – График ЛФЧХ разомкнутой системы
На рисунках 2.6, 2.7, 2.8, 2.9, 2.10 показаны частотных характеристики математической модели (6) разомкнутой системы.