Кинематика точки. Кинематика точки

• Название: Кинематика точки
• Дата: 05.12.2021
• Размер: 0.65 Mb.
• Имя файла: Кинематика точки.docx
• Тип: Документы; #292333
• страница: 2 из 6

Пример 8. При равноускоренном движении тело проходит за два первых равных последовательных промежутка времени по 4,0 с каждый пути s₁ = 24 м и s₂=64 м соответственно. Определите начальную скорость и ускорение тела.

Дано: t₁=t₂= 4,0 с, s₁ =24 м, s₂ = 64 м.

Найти:  .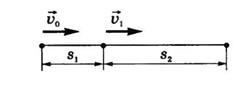



Решение. Запишем уравнения пути для s₁ и (s₁+s₂) соответственно. Так как начальная скорость в этом случае одинакова, то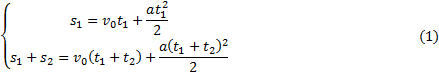


                                               

Так как t1=t2, то

                                                            (2)

Выразив из (1)   и подставив ее в (2), получим:



Тогда начальная скорость 

 

Пример 9. Автомобиль, двигаясь по прямолинейной траектории равноускоренно с начальной скоростью 5,0 м/с, прошел за первую секунду путь, равный 6,0 м. Найдите ускорение автомобиля, мгновенную скорость в конце второй секунды и перемещение за 2,0 с.

Дано: 

Найти: 

Решение. Зная путь, пройденный телом за первую секунду, можно найти ускорение:



Скорость в конце второй секунды найдем по формуле



Перемещение за 2 с можно рассчитать по формулам:



Пример 10. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x = A + Bt + Ct³, где А=4 м, В=2м/с, С=-0,5 м/с³.

Для момента времени t₁=2 c определить: 1) координату точки х₁  точки; 2) мгновенную скорость v₁; 3) мгновенное ускорение а₁.

Дано: x = A + Bt + Ct³, А=4 м, В=2 м/с, С=-0,5 м/с³, t₁=2 c.

Найти: х₁; v₁; а₁.

Решение. 1.Подставим в уравнение движения вместо t заданное значение времени t₁:  x₁ = A + Bt₁ + Ct₁³. Подставим в это выражение значения А, В, С, t₁ и произведем вычисления:  х₁ = 4 м.

2. Мгновенная скорость:   Тогда в момент времени t₁ мгновенная скорость v₁ = B + 3Ct₁². Подставим сюда значения В,С, t₁:   v₁= – 4 м/с. Знак минус указывает на то, что в момент времени  t₁=2 c  точка движется в отрицательном направлении координатной оси.

3. Мгновенное ускорение:   Мгновенное ускорение в момент времени t₁ равно а₁ = 6Сt₁.  Подставим значения С, t₁: а₁= –6 м/с². Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.

 

Пример 11. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = A + Bt + Ct², где А=5 м,  В=4м/с,  С= -1м/с². Определить среднюю скорость v_хср за интервал времени от t₁=1 c до t₂=6 c.

Дано: х = A + Bt + Ct² , А=5м, В=4м/с, С=- 1м/с², t₁=1 c , t₂=6 c.

Найти: v_хср -?   а_хср -?

Решение. Средняя скорость за интервал времени t₂-t₁ определяется выражением v_ср=(х₂-х₁)/(t₂- t₁).

х₁ = A + Bt₁ + Ct₁²= 8 м,        х₂ = A + Bt₂ + Ct₂²= –7 м.

Подставим значения х₁, х₂, t₁ , t₂  и произведем вычисления: v_хср= 3 м/с.

 

Пример 12. Из вертолета,  находящегося на высоте h = 300 м, сбросили груз. Через какое время груз достигнет земли, если: а) вертолет неподвижен; б) вертолет опускается  со скоростью v₀=5 м/с;  3) вертолет поднимается со скоростью v₀=5 м/с. Описать графически соответствующие движения груза в осях s(t), v(t) и a(t).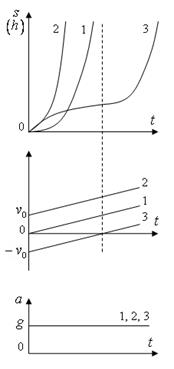



Решение. а) Груз, покинувший неподвижный вертолет, свободно падает, т.е. движется равноускоренно с ускорением свободного падения g. Время движения найдем из соотношения    Откуда    Графики движение объекта отмечены 1 на рисунке.

б) Движение груза, покинувшего вертолет, который опускается с постоянной скоростью v₀=5 м/с, является равноускоренным движением с постоянным ускорением g и описывается уравнением



Подстановка численных значений дает уравнение 9,8t²+10t-600=0.



Отрицательный результат не имеет физического смысла, поэтому время движения t=7,57 с.

Графики движение объекта отмечены 2 на рисунке.

3) Движение груза, покинувшего вертолет, который поднимается с постоянной скоростью v₀=5 м/с, cостоит из двух этапов. На первом  этапе – груз движется равнозамедленно с постоянным ускорением g, направленным противоположно скорости,  и описывается уравнениями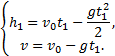



В верхней точке траектории скорость становится равной нулю, поэтому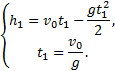



Подставляя второе уравнение системы в первое, получим



На втором этапе  – свободное падение с высоты h₀=h+h₁=300+1,28=301,28 м. 

Поскольку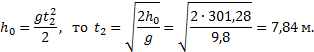



Графики движение объекта отмечены 3 на рисунке.

 

Пример 13. С воздушного шара, опускающегося вниз с постоянной скоростью 2 м/с, бросили вертикально вверх груз со скоростью 18 м/c относительно земли. Определить расстояние между шаром и грузом в момент, когда груз достигает высшей точки своего подъема. Через какое время груз пролетит мимо шара, падая вниз.

Дано: v₀₁= 2 м/с, v₀₂=18 м/c

Найти: s-?  τ -?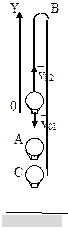



Решение. Направим ось 0Y вертикально  вверх, начало совместим с точкой 0, в которой находился шар в момент бросания груза.    

Тогда уравнения движения груза  и воздушного шара:



Скорость движения груза изменяется по закону v₂=v₀₂ – gt.

В наивысшей точке В подъема груза v₂=0. Тогда  время подъема до этой точки   Координата груза в точке В



За это время воздушный шар опустился до точки А; его координата  



Расстояние между точками А и В: 



Через промежуток времени τ, когда камень пролетит мимо шара, координаты тел будут одинаковы: у_1С=у_2С;     



Отсюда



 

Пример 14. С какой скоростью и по какому курсу должен лететь самолет, чтобы за два часа пролететь на север 300 км, если во время полета дует северо-западный ветер под углом 30^о к меридиану со скоростью 27 км/ч?

Дано: t=7,2∙10³ c;   l=3∙10⁵ м;   α=30° ≈ 0,52 рад;   v₂ ≈7,2 м/с.

Найти: v₂ -?   φ -?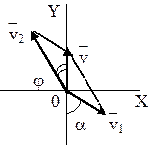



Решение. Рассмотрим движение самолета в системе отсчета, связанной с землей.

Проведем ось ОХ в направлении на восток, а ось OY - на север. Тогда скорость движения самолета в выбранной системе отсчета

                                     (1)

где  v=l/t                                        (2)

Уравнение (1) в проекции на оси

ОХ: 0=v₁∙sinα – v₂∙sinφ;

OY: v= v₂∙cosφ - v₁∙cosα, или   v₁∙sinα = v₂∙sinφ,          v₂∙cosφ=v₁∙cosα + v                 (3)

Разделив  эти уравнения почленно, получим tgφ=v₁sinα/(v₁cosα+ v),  

или с учетом (2)            

tgφ=v₁∙sinα/(v₁∙cosα+ l/t);

φ=arctgv₁∙sinα/(v₁∙cosα+ l/t) ≈0,078 рад.

Возводя в квадрат правые и левые части уравнений (3) и складывая полученные уравнения, находим 

v₂²∙sin²φ + v₂² ∙cos²φ = v₁² sin²α+ (v₁∙cosα + v)²,

откуда  , или с учетом (2)



 

Пример 15. Тело, брошенное вертикально вверх, вернулось на землю через t=3 с. Найти высоту подъема тела и его начальную скорость.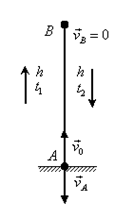



Решение. Движение тела вверх является равнозамедленным с ускорением - g и происходит в течение времени t₁, а движение вниз – равноускоренным с ускорением g и происходит в течение времени t₂.  Уравнения, описывающие движение на участках АВ и ВА, образуют систему: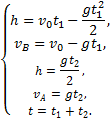 



Поскольку v_B=0, то v₀=gt₁. Подставив v₀ в первое уравнение системы, получим  . Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t₁=t₂=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют v₀=v_A=gt₁=9,8∙1,5=14,7 м/с.

Высота подъема тела



 

Пример 16. Свободно падающее тело в последнюю секунду движения прошло половину пути. Найти высоту, с которой оно брошено и время движения.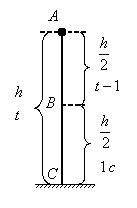



Решение. Зависимость пройденного пути от времени для свободно падающего тела  . Поскольку участок ВС, составляющие половину всего пути,  пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как  .  

 Решая систему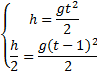



получим t²-4t+2=0. Корни этого уравнения t₁=3,41 с и t₂=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно,  тело падало в течение 3,41 с и прошло за это время путь   

 

Пример 17. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с.

Найти: 1) сколько времени камень будет в движении, 2) на каком расстояниион упадет на землю, 3) с какой скоростью он упадет на землю, 4) какой угол составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать.

Дано: Н=25 м, v_o=15 м/с

Найти: t-?  s_x- ?  v - ? φ- ?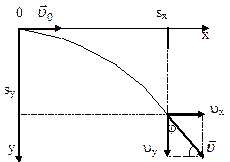



 

Решение. Перемещение брошенного горизонтально камня можно разложить на два: горизонтальное s_x и вертикальное s_y:

s_y=H=gt²/2,    

 s_x=v_ot, 

где t - время движения.

Отсюда: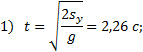    



2)  s_x=v_ot= 33,9 м;        

3)  v_y=gt=22,1м/с;

4)  sinφ= v_y/v=0,827;          

φ=55^о48’.

 

Пример 18. С башни высотой 25 м горизонтально со скоростью v_x=10 м/c брошено тело.

Найти: 1) время t падения тела, 2) на каком расстоянии l от основания башни оно упадет, 3) скорость v в конце падения, 4) угол, который составит траектория тела с землей в точке его приземления.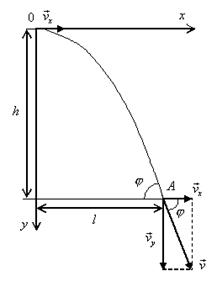



Решение. Движение тела является сложным. Оно участвует в равномерном движении по горизонтали и равноускоренном с ускорением g по вертикали. Поэтому участок АВ описывается уравнениями: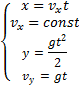



Для точки А эти уравнения принимают вид:



Тогдаl=10∙2,26=22,6 м, а v_y=9,8∙2,26=22,15 м/с.

Поскольку  , то  

Угол, который траектория составляет с землей, равен углу φ в треугольнике скоростей в  т. А, тангенс которого   , поэтому φ=68,7°.

 

Пример 19. Для тела, брошенного с горизонтальной скоростью v_x=10 м/с, через время t=2 с после начала движения найти: нормальное, тангенциальное и полное ускорения, а также радиус кривизны траектории в этой точке.