Кинематика точки. Кинематика точки

• Название: Кинематика точки
• Дата: 05.12.2021
• Размер: 0.65 Mb.
• Имя файла: Кинематика точки.docx
• Тип: Документы; #292333
• страница: 4 из 6

Пример 29. Частица движется в положительном направлении осиx так, что ее ускорение меняется по закону a=α-βx, где α и β - положительные постоянные. Учитывая, что в момент времени t = 0 она покоилась и находилась в начале координат (x₀ = 0), найдем зависимость скорости частицы от координаты.

Решение. Установим уравнения, связывающие а иx.

a=α-βx,                                                            (1)





В эти три уравнения входят четыре переменных: x, v, a, t. Исключим a и t. Выразим из (2)   и подставим в (3):



С учетом выражения (1) получаем дифференциальное уравнение



Разделяя переменные



и производя интегрирование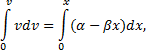



получаем



Искомая зависимость скорости от координаты имеет вид



 

Пример 30. С башни высотой h бросили камень со скоростью v₀ под углом α к горизонту. Найти:

1) какое время камень будет в движении;

2) на каком расстоянии s он упадет на землю;

3) с какой скоростью он упадет на землю;

4) какой угол β составит траектория камня с горизонтом в точке его падения;

5) нормальное и тангенциальное ускорения камня в этой точке, а также радиус кривизны траектории;

6) наибольшую высоту подъема камня.

Сопротивлением воздуха пренебречь.

Решение. На примере этой задачи покажем, как в обобщенном виде можно установить приведенный алгоритм решения любой задачи данного класса.

1. В задаче рассматривается движение материальной точки (камня) в поле силы тяжести Земли. Следовательно, это движение с постоянным ускорением свободного падения g, направленным вертикально вниз.

2. Движение камня рассматривается относительно наблюдателя, находящегося на земле. Движение двумерное - по горизонтали и вертикали. Применим координатный способ описания. Начало координат поместим на поверхности земли, ось х направим горизонтально, ось у - вертикально вверх.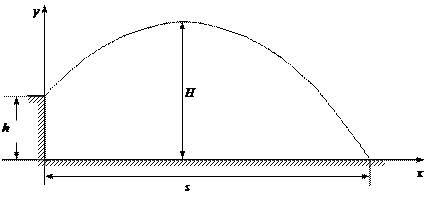



3. В условии задачи рассматривается начальное состояние, состояние А, соответствующее моменту непосредственно перед ударом камня о землю, и состояние В, соответствующее наивысшей точке траектории. Изобразим эти состояния на рисунке и нарисуем векторы скорости в каждом состоянии. Поскольку применяется координатный способ описания, каждый вектор разложим на составляющие. Как было отмечено ранее, вектор ускорения во всех состояниях одинаков и равен g.



 

4. Движение с постоянным ускорением описывается хорошо известными уравнениями: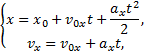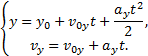





Конкретизируем их для данной задачи. По оси х камень движется из начала координат без ускорения (равномерно) со скоростью v_0x. По оси y камень движется из точки с координатой h с ускорением свободного падения, направленным против оси у и с начальной скоростью v_0у. Отразим эти данные в начальных условиях

x₀=0,       v_0x=v₀cosα,        a_x=0,

y₀=h,       v_0y=v₀sinα,         a_y=-g.

и подставим их в уравнения движения.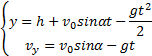





5A. Рассмотрим состояние А. В этом состоянии камень оказался спустя t_A секунд после начала движения. Координаты этой точки равны х_А =s, у_А = 0. На рисунке указаны вектор скорости в этой точке v_A (направленный по касательной к траектории) и его составляющие. Применим уравнения движения к данному состоянию:









В эти четыре уравнения входят следующие неизвестные: t_A , s, v_Аx и v_Аy.

6А. Разрешим полученную систему уравнений относительно указанных неизвестных. Видно, что в уравнение (3) входит одна неизвестная величина - t_A. Решим это квадратное уравнение, преобразовав его предварительно к приведенному виду: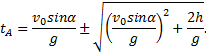





Проанализируем полученный результат. Время не может быть отрицательным, следовательно, отрицательный корень не имеет смысла. Поэтому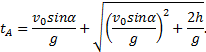



Уравнения (1), (2), (4) позволяют найти все оставшиеся величины: s, v_Аx и v_Аy. Модуль скорости выразим по теореме Пифагора



Из рисунка видно, что          

           

Чтобы найти нормальную и тангенциальную составляющие вектора ускорения, разложим вектор g.



Из рисунка видно, что



Учитывая, что нормальное ускорение связано с модулем скорости соотношением



выразим радиус кривизны траектории в данной точке:



5В. Рассмотрим состояние В. В этом состоянии камень оказался спустя t_В секунд после начала движения. Координаты этой точки равны х_В, у_В = H. На рисунке указан вектор скорости в этой точке v_В, направленный горизонтально по оси х. Следовательно, вертикальная составляющая скорости равна нулю v_Вy =0. Применим уравнения движения к данному состоянию:









Время t_В найдем из уравнения (4)



а максимальную высоту подъема - из уравнения (3)





Видно, что уравнения (1) и (2) не потребовались при решении этой задачи.

 

Пример 31. Трамвай движется прямолинейно от остановки А до следующей остановки В с ускорением, меняющимся по закону a=α-βx, где α и β - положительные постоянные, х - расстояние между трамваем и остановкой А. Найти расстояние между остановками и максимальную скорость трамвая.

Решение. Решим задачу в соответствии с установленным алгоритмом.

1) Трамвай можно считать материальной точкой, которая движется по прямолинейной траектории. Отличительной чертой его движения является заданная в условии задачи зависимость ускорения от координаты.

2) Применим координатный способ описания движения. Совместим начало координат с остановкой А. Отметим положение остановки В и тоски С, в которой скорость трамвая максимальна.

 



 

3) Установим, какая информация о координатах, скоростях, ускорениях содержится в условии задачи, какую требуется определить. В начальном и конечном состояниях скорости равны нулю, а в состоянии С скорость максимальна, поэтому ускорение (производная скорости по времени) равно нулю.

Состояния объекта и их характеристики	Точка А t = 0	Точка С t = tC	Точка В t = tB
Координаты	x0 = 0	-	xB = s - ?
Скорости	v0 = 0	vC = vmax - ?	vB = 0
Ускорения	-	aC = 0	-

4) В условии задана зависимость ускорения от координаты

a=α-βx,                                     (1)

известны или требуют нахождения значения координаты и скорости в состояниях В и С. Следовательно, необходимо уравнение, связывающее v и x.



5) Применим кинематические уравнения к состоянию В. Подставим в уравнение (2) соответствующие значения координаты и скорости



Поскольку в состоянии В s≠0, то 2α-βs=0, откуда    

Применим кинематические уравнения к состоянию С. Подставим в уравнения (1) и (2) соответствующие значения координаты и ускорения.

a_C=0=α-β∙x_C,                                     (1a)



Из (1а) выразим координату точки С

и подставим в уравнение (2а):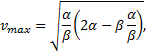



Откуда



 

Вопросы для самопроверки

- Что изучает кинематика?

- Какие задачи решает кинематика точки и твердого тела?

- В чем различие между телом отсчета и системой отсчета?

- Что понимают под системой отсчета? системой координат? радиус-вектором?

- Дайте определение основных кинематических характеристик движения.

- Что такое "алгебраическая" скорость точки? В каком направлении происходит движение точки при положительном и отрицательном значении алгебраической скорости?

- В чем отличие естественных осей координат от декартовых?

- Какие кинематические величины зависят от выбора системы отсчета? одинаковы в различных системах отсчета?

- Может ли человек, находясь на движущемся эскалаторе метро, быть в покое в системе отсчета, связанной с поверхностью Земли?

- Совпадает ли направление ускорения с направлением скорости материальной точки при равноускоренном движении? при равнозамедленном движении?

- Какие кинематические характеристики движения остаются постоянными при равномерном прямолинейном движении? при равноускоренном движении?

- Какие величины, характеризующие движение, можно определить по графику скорости?

- Два поезда идут навстречу друг другу; один ускоренно на север, другой замедленно на юг. Как будут направлены векторы ускорений поездов?

- Чем отличаются движения, уравнения которых приведены x₁=3-5t-2t²;   x₂=-3+5t-2t²?

- Какие существуют способы описания движения материальной точки?

- Перечислите основные способы задания движения точки.

- Дайте определение скорости и ускорения точки при векторном способе задания ее движения.

- Дайте определение скорости и ускорения точки при координатном способе задания ее движения.

- Как определяется характер движения точки при векторном способе задания ее движения?

- Как определяется характер движения точки при координатном способе задания ее движения?

- Каковы условия ускоренного, замедленного движения точки при естественном способе задания ее движения?

- Запишите и покажите на рисунке связь между векторами полного, нормального и касательного ускорений.

- Движение точки задано в полярной системе координат. Как найти уравнение ее траектории?

- Что должно быть известно при естественном способе задания движения точки?

- Какие кинематические способы задания движения точки существуют и в чем состоит каждый из этих способов?

- Запишите в общем виде закон движения в естественной и координатной форме?

- Как разложить вектора скорости и ускорения точки по осям естественного трехгранника?

- Запишите формулы для скорости, касательного и нормального ускорений точки через дуговую координату.

- Как найти проекции ускорения точки на оси естественной системы координат?

- Что называют траекторией движения?

- Как определяется скорость движения при естественном способе задания движения?

- В чем различие понятий "путь" и "дуговая координата"?

- Запишите формулы для определения касательного, нормального и полного ускорений.

- При каких условиях вектор полного ускорения совпадает с вектором: а) нормального ускорения; б) касательного ускорения?

- Что характеризует касательное ускорение и как оно направлено по отношению к вектору скорости?

- Чему равно скалярное произведение векторов скорости и нормального ускорения точки?

- При каких условиях значение дуговой координаты точки в некоторый момент времени равно пути, пройденному точкой за промежуток от начального до данного момента времени?

- Чем является траектория точки при векторном способе задания движения точки?

- Как по уравнениям движения точки в координатной форме определить ее траекторию?

- Сформулируйте теорему о проекции производной вектора на неподвижные координатные оси.

- Приведите определения соприкасающейся, спрямляющей и нормальной плоскостей.

- Как выбираются направления единичных векторов касательной, нормали и бинормали?

- Запишите формулу для определения модуля вектора кривизны плоской кривой.

- Что называется перемещением точки за фиксированный промежуток времени?

- Как направлена средняя скорость точки за некоторый промежуток времени?

- Какие существуют способы определения скорости движения точки?

- Запишите формулы, определяющие модуль и направление скорости точки при координатном способе задания ее движения.

- Как выражается скорость точки через криволинейную координату при естественном способе задания движения?

- Дайте определение среднего ускорения точки за некоторое время.

- Как выражаются модуль и направляющие косинусы вектора ускорения точки через проекции ускорения на прямоугольные координатные оси?

- Как классифицируется движение точки по ускорениям?

- В каких случаях движение точки обращаются в нуль: а) касательное ускорение; б) нормальное ускорение; в) полное ускорение?

- В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?

- Как найти проекции ускорения точки на оси неподвижной системы координат Декарта?

- Запишите формулы для нормального и касательного ускорений при естественном способе задания движения.

- Чему равен вектор скорости точки в данный момент времени и какое направление он имеет?

- Как связан орт касательной к кривой с радиусом-вектором движущейся точки?

- Чему равна проекция скорости точки на касательную к ее траектории и модуль ее скорости?

- Как определяются проекции скорости точки на неподвижные оси декартовых координат?

- Что представляет собой годограф скорости и каковы его параметрические уравнения?

- Какой вид имеет годограф скорости прямолинейного неравномерного движения и равномерного движения по кривой, не лежащей в одной плоскости?

- Чему равен вектор ускорения точки и как он направлен по отношению к годографу скорости?

- Как направлены естественные координатные оси в каждой точке кривой?

- Каковы модуль и направление вектора кривизны кривой в данной точке?

- В какой плоскости расположено ускорение точки и чему равны его проекции на естественные координатные оси?

- Что характеризует собой касательное и нормальное ускорения точки?

- При каком движении точки равно нулю касательное ускорение и при каком - нормальное ускорение?

- Как классифицируются движения точки по ускорениям?  

- В какие моменты времени нормальное ускорение в криволинейном движении может обратиться в нуль?

- В какие моменты времени касательное ускорение в неравномерном движении может обратиться в нуль?

- Чем отличается график пути от графика движения точки?

- Как по графику движения определить алгебраическое значение скорости точки в любой момент времени?

- Как по графику скорости прямолинейного движения точки определить алгебраическое значение ускорения точки в любой момент времени?

- Запишите формулу ускорения при прямолинейном движении?

- Запишите формулу ускорения (полного) при криволинейном движении.

- Сравните время падения тела, брошенного горизонтально с некоторой высоты и свободно падающего с той же высоты.

- Три тела брошены так: первое — вниз без начальной скорости, второе — вниз с начальной скоростью, третье — вверх. Что можно сказать об ускорениях этих тел при их движении?

- Как будет изменяться дальность полета снарядов при увеличении угла наклона орудия к горизонту?

- Как направлено ускорение при криволинейном движении?

- Как направлена мгновенная скорость материальной точки при криволинейном движении?

- Является ли движение по окружности с постоянной по модулю скоростью равноускоренным?

- Автомобиль движется на повороте. Одинаковые ли расстояния проходят при этом правые и левые колеса автомобиля?

- Велосипедист движется по прямолинейному участку дороги со скоростью   (см.рис.). С какой скоростью движутся точки А, В, С, D колеса велосипеда относительно оси? относительно дороги?