Кинематика точки. Кинематика точки

• Название: Кинематика точки
• Дата: 05.12.2021
• Размер: 0.65 Mb.
• Имя файла: Кинематика точки.docx
• Тип: Документы; #292333
• страница: 3 из 6

Решение. Вертикальная составляющая скорости v_y=gt=9,8∙2=19,6 м/с

Скорость в точке А:

, то  

Векторы   образуют треугольник скоростей, а векторы   - треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны:  .

Отсюда,  





Нормальное ускорение  , поэтому радиус кривизны траектории



 

Пример 20. Мяч бросили со скоростью 10 м/с под углом 40^о к горизонту.

Найти: 1) на какую высоту поднимется мяч; 2) на каком расстоянии от места бросания мяч упадет на землю, 3) сколько времени он будет в движении.

Дано: v_o=10 м/с, α=40^о.

Найти: s_y - ?  s_x - ?  t - ?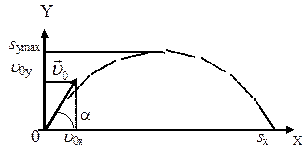



Решение.  1) Найдем наибольшую высоту s_y max, на которую поднимается тело, брошенное со скоростью v_o  подуглом α к горизонту. Имеем (см. рис.):               

v_y=v_o sinα – gt;                         (1)

s_y=v_ot∙sinα – gt²/2.                    (2)

В верхней точке v_y=0  и из (1) получим v_o∙sin𝛼 = gt₁, отсюда время подъема мяча t₁=v_o∙sinα/g. Подставляя t₁ в (2), получим

s_y max= v_o² ∙sin²α/(2g)= 2,1 м.

2) Найдем дальность полета s_x max  тела, брошенного под углом к горизонту.

Имеем: v_x=v_o∙cosα,                 (3)

s_x=v_xt=v_ot∙cosα.                    (4)

Тело упадет на горизонтальную плоскость через время t₂=2t₁=2v_osinα/g.

Подставляя t₂ в (4), получим  s_xmax = v_о²sin2α/g=10,0 м.

3) t₂=2t₁=2v_osinα/g=1,3 с.

 

Пример 21. Тело брошено со скоростью v₀=10 м/с² под  углом α=30° к горизонту. На какую высоту  тело поднимется. На каком расстоянии от места бросания оно упадет на землю? Какое время он будет в движении?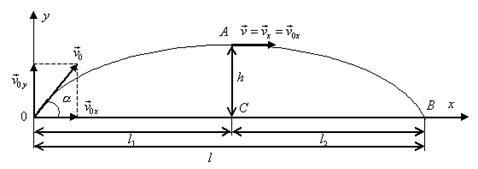



Решение. Горизонтальная и вертикальная составляющие начальной скорости





Движение на участке ОА можно разложить на два простых движения: равномерное по горизонтали и равнозамедленное по вертикали: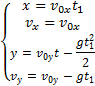



В точке А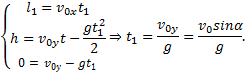      



Тогда    и     

Если тело участвует одновременно в нескольких движениях, то в каждом из них оно участвует независимо от другого, следовательно, время движения на участке АВ определяется временем движения вниз – t₂. Время движения вверх равно времени движения вниз, а,  значит,   

При равномерном движении по горизонтали за равные промежутки времени тело проходит равные участки пути, следовательно,



Дальность полета



Высота подъема тела



 

Пример 22. Точка движется прямолинейно на плоскости по закону x=4(t-2)². Каковы начальная скорость v₀ и ускорение точки a? Найти мгновенную скорость точки v_t=5 в начале пятой секунды движения.

Решение.

1) Т.к. v=x’,  то  v₀=(4∙(t-2)²)’=(4∙(t²-4t+4))’=(4t²-16t+16)’=8t-16

       при t=0     v₀=-16 м/с.

2) Т.к. a= , то a=(8t-16)’=8 м/с.

3) При t=4, т.к. до начала 5 с прошло 4 с.

   v_t=5=8t-16=8∙4-16=32 м/с.

Ответ: Начальная скорость точки v₀=-16 м/с, ускорение a=8 м/с, скорость точки в начале пятой секунды движения v_t=5=32 м/с.

 

Пример 23. Движение материальной точки описывается уравнениями: а) s=αt³; б) s=αt²+βt. Сравните среднюю скорость   и среднеарифметическую начальной и конечной скоростей v_ср в интервале времени 0 - t. Здесь α и β - положительные постоянные.

Решение. Вспомним определения средней и мгновенной скорости:



Выражения для мгновенной скорости получаются путем дифференцирования уравнения движения.



Выражения для средней скорости находятся как отношение изменения криволинейной координаты к времени:



Получим выражения для среднеарифметической скорости:



Ответим на вопрос условия задачи. Видно, что в случае “а” средняя и среднеарифметическая скорости не совпадают, а в случае “б” - совпадают.

 

Пример 24. Материальная точка движется равномерно по криволинейной траектории. В какой точке траектории ускорение максимально?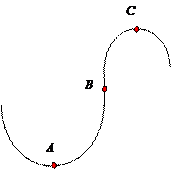



 

Решение. При движении по криволинейной траектории ускорение складывается из тангенциального и нормального. Тангенциальное ускорение характеризует быстроту изменения величины (модуля) скорости. Если величина скорости не изменяется, тангенциальное ускорение равно нулю. Нормальное ускорение зависит от радиуса кривизны траектории a_n=v²/R. Ускорение максимально в точке с наименьшим радиусом кривизны, т.е. в точке С.

 

Пример 25. Материальная точка движется согласно закону: 

1) Определить начальную координату, начальную скорость и ускорение путем сравнения с законом движения с постоянным ускорением. Записать уравнение для проекции скорости.

Решение. Закон движения с постоянным ускорением имеет вид



Сравнивая это уравнение с уравнением условия задачи, получаем

x₀ = - 1 м,

v_0x = 1 м/с,

a_x = - 0,25 м/с².

Возникает вопрос: какой смысл имеет знак “минус”? Когда проекция вектора отрицательна? Только в том случае, когда вектор направлен против оси координат.

Изобразим на рисунке начальную координату, векторы скорости и ускорения.

 



Запишем уравнение для скорости в виде



и подставим в него полученные данные (начальные условия)



 

2) Найти зависимость скорости и ускорения от времени, применяя определения этих величин.

Решение. Применим определения для мгновенных значений скорости и ускорения:



Производя дифференцирование, получим  v_x=1-0,25t,    a_x = - 0,25 м/с².

Видно, что ускорение не зависит от времени.

 

3) Построить графики v_х(t) и a_х(t). Охарактеризовать движение на каждом участке графика.

Решение. Зависимость скорости от времени - линейная, график представляет собой прямую линию.

При t = 0 v_х = 1 м/с. При t = 4 с v_х = 0.



 

Из графика видно, что на участке “а” проекция скорости положительная, а ее величина убывает, т.е. точка движется замедленно в направлении оси х. На участке “b” проекция скорости отрицательная, а ее модуль возрастает. Точка движется ускоренно в направлении, противоположном  оси х. Следовательно, в точке пересечения графика с осью абсцисс происходит поворот, изменение направления движения.

 

4) Определить координату точки поворота и путь до поворота.

Решение. Еще раз отметим, что в точке поворота скорость равна нулю. Для этого состояния из уравнений движения получаем:





Из второго уравнения получаем t_пов = 4 с. (Видно, чтобы получить это значение не обязательно строить и анализировать график). Подставим это значение в первое уравнение: x_пов=-1+4-4²/8 = 1 м. Изобразим, как двигалась точка.

 



 

Путь до поворота, как видно из рисунка, равен изменению координаты: s_пов=x_пов-x₀=1-(-1)=2 м.

 

5) В какой момент времени точка проходит через начало координат?

Решение. В уравнении движения следует положить х = 0. Получаем квадратное уравнение 0=-1+t-t²/8 или t²-8t+8=0. У этого уравнения два корня:  . t₁ = 1,17 с, t₂ = 6,83 с. Действительно, точка проходит через начало координат два раза: при движении “туда” и “обратно”.

 

6) Найти путь, пройденный точкой за 5 секунд после начала движения, и перемещение за это время, а также среднюю путевую скорость на этом участке пути.

Решение. Прежде всего найдем координату, в которой оказалась точка после 5 секунд движения и отметим ее на рисунке.

x(5)=-1+5-5²/8= 0,875 м.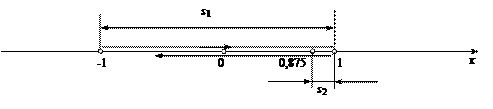

 



 

Поскольку в данном состоянии точка находится после поворота, то пройденный путь уже не равняется изменению координаты (перемещению), а складывается из двух слагаемых: пути до поворота

s₁ = x_пов - x₀ = 1 - (-1) = 2 м

и после поворота

s₂ = x_пов - x(5)  = 1 - 0,875 = 0,125 м,

s = s₁ + s₂ = 2,125 м.

Перемещение точки равно

s_х = x(5) - x₀ = 0,875 - (-1) = 1,875 м

Средняя путевая скорость вычисляется по формуле



В рассмотренной задаче описан один из наиболее простых видов движения - движение с постоянным ускорением. Тем не менее, данный подход к анализу характера движения является универсальным.

 

Пример 26. При одномерном движении с постоянным ускорением зависимости координаты и скорости частицы от времени описываются соотношениями: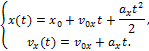



Установить связь между координатой частицы и ее скоростью.

Решение. Из этих уравнений исключаем время t. Для этого используем метод подстановки. Из второго уравнения выражаем время   и подставляем в первое уравнение:



Если движение начинается из начала координат (х₀ =0) из состояния покоя (v_0x =0), то полученная зависимость принимает вид



хорошо знакомый из школьного курса физики.

 

Пример 27. Движение материальной точки описывается уравнением:  , где i и j - орты осей х и у, α и β - положительные постоянные. В начальный момент времени частица находилась в точке х₀ =у₀=0. Найти уравнение траектории частицы у(х).

Решение. Условие задачи сформулировано с применением векторного способа описания движения. Перейдем к координатному способу. Коэффициенты при единичных векторах представляют собой проекции вектора скорости, а именно:



Вначале получим зависимости x(t) и y(t), решая задачу первого класса.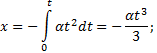









Из полученных уравнений исключим времяt. Из первого уравнения  . Из второго уравнения получаем



Обратим внимание, что координата х должна быть отрицательной, что соответствует положительным значениям времени t.

 

Пример 28. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону  , где α - положительная постоянная. Учитывая, что в момент времениt = 0 она находилась в начале координат (x₀ = 0), найти зависимость от времени скорости частицы.

Решение. Установим уравнения, связывающие v и x.

По условию задачи  . В тоже время можно записать  .

Отсюда    (ее исключить проще всего). Получилось дифференциальное уравнение с разделяющимися переменными.

Разделяя переменные   и интегрируя от 0 до t и от 0 до х,  , получаем:  , откуда находим зависимость координаты от времени



Искомую зависимость скорости от времени можно получить, применяя любое из двух исходных уравнений. Например,