Задачи. Метод-указ-для-заочн. Класичне означення ймовірності
 Скачать 58.88 Kb. Скачать 58.88 Kb.
|
|
Завдання контрольної роботи з ТЕОРІЇ ЙМОВІРНОСТЕЙ ТА МАТЕМАТИЧНОЇ СТАТИСТИКИ для студентів ЕТІ заочної форми навчання Тема «Класичне означення ймовірності» 1.Бухгалтер щодня заповнює 8 документів, 3 з яких потребують подальшого опрацювання. Головний бухгалтер регулярно перевіряє 2 довільно обраних документи. Знайти ймовірність того, що він перевірить: а) документи, що потребують подальшого опрацювання; б) документи, що не потребують подальшого опрацювання; в) тільки один з документів, що потребує подальшого опрацювання. 2. PIN-код банківської картки складається з 4-х цифр. а) Скільки існує різних варіантів коду? б) Яка ймовірність вгадати код? Тема «Теореми додавання та множення ймовірностей». 3.Для сигналізації про аварію встановлені 2 незалежно працюючих сигналізатори. Ймовірність того, що при аварії спрацює перший сигналізатор, дорівнює 0,95, другий - 0,9. Знайти ймовірність того, що при аварії: а) спрацює тільки перший сигналізатор; б) спрацює тільки другий сигналізатор; в) спрацюють обидва сигналізатора; г) спрацює тільки один сигналізатор. Тема «Формула повної ймовірності. Формула Байєса». 4. На ринку цінних паперів фіксується позитивна динаміка змін з відносною частотою 0,4, негативна - з відносною частотою 0,5 і відсутність динаміки змін - з відносною частотою 0,1. Статистичні спостереження показують, що фірма отримує суттєвий дохід з ймовірністю 0,9 при позитивній динаміці, з ймовірністю 0,2 при негативній динаміці і з ймовірністю 0,8 при відсутності динаміки. Знайти ймовірність того, що в довільний час фірма отримає суттєвий дохід. (Вказівка: використати формулу повної ймовірності) 5. В умовах попередньої задачі відомо, що фірма отримала суттєвий дохід. Знайти ймовірність того, що на ринку цінних паперів спостерігалася: а) позитивна динаміка змін; б) негативна динаміка змін; в) динаміка змін була відсутня. (Вказівка: використати формулу Байєса) Тема «Схема Бернуллі. Формула Бернуллі» 6.Кожен з 4-х незалежних аудиторів надає дієву допомогу в оформленні бухгалтерської документації з ймовірністю 0,6. Знайти ймовірність того, що дієву допомогу нададуть: а) два аудитори; б) більше двох аудиторів; в) менше двох аудиторів. Тема «ТЕОРЕМИ МУАВРА-ЛАПЛАСА» Локальна теорема Муавра-Лапласа Ймовірність того, що в n незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює p (0 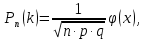 де 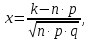 а значення парної функції 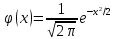 можна знайти у відповідній таблиці. Інтегральна теорема Муавра-Лапласа Ймовірність того, що в n незалежних випробуваннях, в кожному з яких ймовірність появи події дорівнює p (0 P(k1, k2) = Ф(х2) – Ф(х1), де 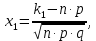 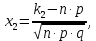 а значення функції Лапласа (яка є непарною) можна знайти у відповідній таблиці. Приклад. Ймовірність появи події А в кожному зі 100 незалежних випробувань постійна і дорівнює р=0,8. Знайти ймовірність того, що подія А з’явиться: а) 75 раз; б) не менше 75 раз і не більше 90 раз; в) не менше 75 раз; г) не більше 74 раз. Розв’язання. а) за локальною теоремою Муавра-Лапласа 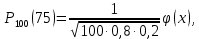 де 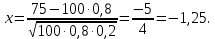 З таблиці функції φ(x) φ (–1,25) = 0,1826. Тоді 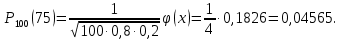 б) за інтегральною теоремою Муавра-Лапласа 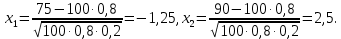 Оскільки функція Лапласа непарна, то Ф(х1) = Ф(–1,25) = –0,3944, Ф(х2) = Ф(2,5) = 0,4938. Шукана ймовірність Р100(75; 90) = 0,4938 + 0,3944 = 0,8882. в) вимога, щоб подія А з’явилася не менше 75 раз, означає, що число появ події А може бути 75, 76, … , 100. Тому за інтегральною теоремою Муавра-Лапласа 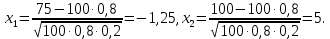 По таблиці значень функції Лапласа Ф(х1) = Ф(–1,25) = –0,3944, Ф(х2) = Ф(5) = 0,5. Шукана ймовірність Р100(75; 100) = 0,5 + 0,3944 = 0,8944. г) вимога, щоб подія А з’явилася не більше 74 раз, означає, що число появ події А може бути 0, 1, … , 74. Події «не менше 75 раз» і «не більше 74 раз» протилежні, тому Р100(0; 74) = 1 – Р100(75; 100) = 0,1056. Завдання контрольної роботи 7.Товар постачається партіями по 200 виробів. Ймовірність пошкодження виробу при транспортуванні постійна і дорівнює 0,05. За локальною теоремою Муавра-Лапласа знайти ймовірність того, що при транспортуванні буде пошкоджено 10 виробів. За інтегральною теоремою Муавра-Лапласа знайти ймовірність того, що буде пошкоджено: а) менше 10 виробів; б) більше 10 виробів. Тема «ДИСКРЕТНІ ВИПАДКОВІ ВЕЛИЧИНИ» Дискретною називають випадкову величину, яка може приймати відокремлені ізольовані одне від одного числові значення з відповідними ймовірностями. Іншими словами, можливі значення дискретної випадкової величини можна пронумерувати. Число можливих значень дискретної випадкової величини може бути скінченним або нескінченним. Приклад 1. Х – кількість відвідувачів офісу, які можуть одночасно знаходитися в офісі під час епідемії коронавірусу. Х – випадкова величина, тому що заздалегідь невідомо, якою саме буде ця кількість в довільний момент. Це дискретна випадкова величина, оскільки вона може приймати окремі значення: 0, 1, 2, , n (n - максимально можлива кількість відвідувачів, обмежена площею офісу). Ймовірності цих значень вираховуються за статистичними спостереженнями. Приклад 2. Х – кількість спроб вгадати забутий код замка власної валізи – випадкова величина, оскільки заздалегідь невідома кількість спроб, яка призведе до потрібного коду. Х – це дискретна випадкова величина, оскільки вона може приймати нескінченне число ізольованих значень, які можна занумерувати: 0, 1, 2, …і так далі до нескінченності, якщо власник чемодану буде робити спроби хаотично, без певного алгоритму. Ймовірності цих значень можна визначити також за статистичними спостереженнями. Приклад 3. Х – час, потрібний для обслуговування клієнта офісу – випадкова величина, оскільки заздалегідь невідомий час обслуговування довільного клієнта. Якщо цей час вимірюється теоретично, тобто часу обслуговування клієнта ставиться у відповідність точка на відрізку [0; tmax] (tmax максимально можливий час обслуговування), то Х – не дискретна випадкова величина, оскільки, всі її значення, тобто кількість точок на відрізку [0; tmax], не можна занумерувати. Якщо ж час вимірювати практично, з точністю, наприклад, до годин, то Х – дискретна випадкова величина. Законом розподілу дискретної випадкової величини називають перелік її можливих значень з відповідними їм ймовірностями. Закон розподілу дискретної випадкової величини Х може бути заданий у вигляді таблиці, перший рядок якої містить можливі значення хі, а другий – ймовірності рі:
Закон розподілу дискретної випадкової величини Х може бути також заданий аналітично (у вигляді формули) або графічно. Основні закони розподілу дискретних випадкових величин Біноміальний закон розподілу Біноміальним називають закон розподілу дискретної випадкової величини Х – числа хі випадків появи події в схемі Бернуллі (в n незалежних випробуваннях, в кожному з яких ймовірність р події однакова). Нагадаємо, що ймовірності рk того, що в n випробуваннях подія з’явиться k раз, шукаються за формулою Бернуллі 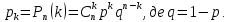 Ця формула використовується при невеликих n. Закон розподілу Пуассона Якщо n досить велике, а ймовірність р появи події в кожному випробуванні дуже мала (р < 0,1), то використовують наближену формулу 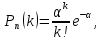 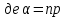 – середнє число появ події в n випробуваннях. – середнє число появ події в n випробуваннях.В цьому випадку говорять, що випадкова величина розподілена за законом Пуассона. Закон розподілу Пуассона використовують у задачах статистичного контролю якості, в теорії надійності, теорії масового обслуговування, для обчислення кількості вимог на виплату страхових сум тощо. Висновок. Порівнюючи ймовірності, обчислені за формулою Пуассона і теоремами Муавра-Лапласа, можна спостерігати суттєву їх різницю. Це пояснюється тим, що формулу Пуассона є сенс застосовувати у випадках, коли середнє число появ події в n випробуваннях є величиною, близькою до постійної; на відміну від того, що теореми Муавра-Лапласа є сенс застосовувати, коли ймовірність появи події в n випробуваннях постійна. Приклад 4. Товар постачається партіями по 500 виробів. Ймовірність пошкодження виробу при транспортуванні дорівнює 0,002. Знайти ймовірність того, що при транспортуванні буде пошкоджено 3 вироби. Розв’язання. Число n=500 велике, ймовірність p=0,002 мала і вказані події (пошкодження виробу) незалежні, тому можна застосувати формулу Пуассона. Знайдемо α: α = np = 500·0,002 = 1. Знайдемо ймовірність того, що буде пошкоджено k=3 виробів: 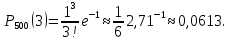 Приклад для самостійної роботи. Товар постачається партіями по 500 виробів. Ймовірність пошкодження виробу при транспортуванні дорівнює 0,002. За формулою Пуассона знайти ймовірності того, що при транспортуванні буде пошкоджено виробів: а) менше трьох; б) більше трьох; в) хоча б один. Рекомендація: Для більш точної відповіді бажано прийняти е–1=0,36788. а) за формулою Пуассона знайдіть окремо ймовірності Р500(0), Р500(1) і Р500(2), а потім їх додайте. Перевірте відповідь: 0,9197. б) події «більше трьох» і «не більше трьох» протилежні, тому сума їх ймовірностей дорівнює одиниці. Відтак, потрібно знайти ймовірність події «не більше трьох» Р500(0) + Р500(1) + Р500(2) + Р500(3) і відняти її від одиниці. Перевірте відповідь: 0,019. в) події «хоча б один» і «ні один, тобто нуль пошкоджених» протилежні, тому сума їх ймовірностей дорівнює одиниці. Відтак, ймовірність Р500(0) треба відняти від одиниці. Перевірте відповідь: 0,632. Завдання контрольної роботи 8.Товар постачається партіями по 400 виробів. Ймовірність пошкодження виробу при транспортуванні дорівнює 0,005. За формулою Пуассона знайти ймовірності того, що при транспортуванні буде пошкоджено виробів: а) менше трьох; б) більше трьох; в) хоча б один. Тема: «ЧИСЛОВІ ХАРАКТЕРИСТИКИ ДИСКРЕТНОЇ ВИПАДКОВОЇ ВЕЛИЧИНИ» Математичним сподіванням дискретної випадкової величини називають суму добутків всіх її можливих значень на їх ймовірності: М(Х) = х1р1 + х2р2 + … + xnpn . Аналогом математичного сподівання в математичній статистиці є середнє значення. Дисперсією дискретної випадкової величини називають математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання: D(X) = M(X – M(X))2. Дисперсію зручно обчислювати за формулою: D(X) = M(X2) – M2(X). Дисперсія в математичні статистиці показує відхилення випадкової величини від середнього значення. Яскравим прикладом ролі дисперсії служить відомий приклад з двома лікарняними палатами, в кожній з яких знаходяться по 2 пацієнти. Температура пацієнтів першої палати: _______35°_____ _____37°_________ Температура пацієнтів другої палати: __32°_________________ ___________________40°__ Математичне сподівання температури (середня температура) пацієнтів обох палат однакове: М(Х) = 36°, але значно більше відхилення від математичного сподівання у пацієнтів другої палати свідчить про кардинальну різницю стану «пацієнтів» другої палати. Про це свідчить дисперсія, яка у другому випадку значно більша за дисперсію у першому. Оскільки дисперсія виміряє відхилення від середнього у квадратних одиницях (у градусах в квадраті з попереднього приклада), то вводять наступну числову характеристику. Середнім квадратичним відхиленням дискретної випадкової величини називають квадратний корінь з дисперсії: 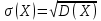 . .Приклад 1. Знайти числові характеристики дискретної випадкової величини Х, заданої законом розподілу:
Розв’язання. Математичне сподівання M(X) = – 4·0,2 + 6·0,3 + 10·0,5 = – 0,8 + 1,8 + 5 = 6. Дисперсія D(X) = (– 4)2·0,2 + 62·0,3 + 102·0,5 – 62 = 3,2 + 10,8 + 50 – 36 = 28. Середнє квадратичне відхилення 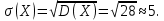 Завдання контрольної роботи 9. Знайдіть за вказаними формулами числові характеристики випадкової величини Х – кількості відвідувачів офісу, які можуть одночасно знаходитися в офісі під час епідемії коронавірусу:
10. Знайдіть за вказаними формулами числові характеристики випадкової величини Х – кількості спроб (до заблокування банкомату) вгадати забутий PIN-код картки:
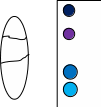
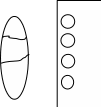
РОЗДІЛ «ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ» Математична статистика – розділ математики, в якому розглядаються математичні методи обробки масивів статистичних даних. Не плутайте з предметом «Статистика», в якому статистичні дані обробляються з економічної точки зору. Тема: «ШКАЛИ ВИМІРІВ В МАТЕМАТИЧНІЙ СТАТИСТИЦІ» Для застосування методів математичної статистики потрібно визначити, як саме описати статистичні дані перед їх обробкою. Найбільш вживаний спосіб – опис статистичних даних числами. Але є інші способи, які в підсумку можуть зводитися до числової обробки. Ми розглянемо найбільш вживані способи опису статистичних даних – опис статистичних даних у чотирьох шкалах виміру. Означення. Шкалою досліджуваної властивості (показника, ознаки) називається формалізований образ видів (значень) цієї властивості, які хоче розглянути дослідник. Шкали різних властивостей, об’єднані за способом формалізації, визначають їх класифікацію. Розглянемо сутність 4-х основних видів шкал і приклади їх застосування. Шкала найменувань (номінальна шкала) ставить у відповідність досліджуваним об’єктам їх символи (назви; числа, що слугують тільки ярликами об’єкта, тощо). При цьому досліджувані об’єкти «виміру» розпадаються на множину класів (категорій, видів, значень), що не перетинаються. Різні об’єкти можуть досліджуватися, наприклад, за однією з чотирьох властивостей – за кольором, за формою, за розміром або за попитом (Рис. 1). Так, наприклад, за кольором об’єкти можуть розпадатися на червоні, зелені, жовті і т.д. З об’єктами, що «вимірюються» за шкалою найменувань, можна виконувати тільки операцію порівняння – чи співпадають вони (наприклад, за кольором), чи ні. За результатами такої перевірки можна обраховувати наповненість (частоту, ймовірності) для різних класів, яка може використовуватись для застосування різних методів статистичного аналізу.
Рис. 1. Схематичне зображення шкали найменувань (зліва) і шкали рангів (справа). Приклади використання шкали найменувань. Приклад 1. Очевидний приклад шкали найменувань – шкала ознаки студента за спеціальністю його навчання. Наприклад:
Приклад 2. В наступному прикладі досліджується група студентів, яка закінчила вивчення даної дисципліни. Треба охарактеризувати кожного студента за ознакою: наявність у нього знань, умінь та навичок, задекларованих в програмі дисципліни. Припустимо, що кожна з ознак визначається тільки за двома критеріями – має чи не має цю ознаку студент. Тоді одним із прикладів шкали характеристики може бути упорядкована множина трьох символів, перший з яких свідчить про наявність знань (З) або відсутність ( – ) знань, другий – про наявність умінь (У) або відсутність ( – ) умінь, третій – про наявність (Н) або відсутність ( – ) навичок: {ЗУН, ЗУ–, З–Н, –УН, З– –, –У–, – –Н, – – –}.
Це також шкала найменувань. За нею можна поділити студентів на 8 груп, в кожній з яких студенти мають однакове значення досліджуваного комплексу ознак. Природньо, не кожну пару цих груп студентів можна порівняти одна з одною за успішністю вивчення даної дисципліни. Але так, як і в першому прикладі, можна порівняти студентів за приналежністю до конкретної групи і порахувати кількість студентів в кожній з груп. Порядкова шкала (шкала рангів)містить упорядковані відображення видів досліджуваної властивості. Порядок може описуватися розташуванням в множині видів (вищого рівня, найбільш виражено, більш привабливо тощо) або рангами, якими нумерують місця видів. В ранговій шкалі разом з можливостями номінальної шкали є також можливість порівняння видів, тобто їх рангів. Приклади використання порядкової шкали. Приклад 1. Оцінки експертів часто виражаються саме в порядковій шкалі. Наприклад, студент може розташувати імена викладачів за порядком оцінки ним викладача - «Який викладач більш доброзичливий?»: викладач А найбільш доброзичливий, викладач Б трохи менш доброзичливий, … викладач Р найбільш недоброзичливий. Приклад 2. За властивістю студента мати проявлені ним лідерські якості студентів можна розташувати за рангами: студент А найбільше проявив лідерські якості, студент В має порівняно зі студентом А менш виражені лідерські якості, … студент Л пливе за течією, тобто не проявив лідерські якості. Результатом опитування чи іншого способу визначення лідерських якостей може бути рейтинговий список студентів, складений у порядку зменшення вираженості цих якостей. Шкалою тут буде множина всіх перестановок прізвищ студентів. Наприклад, якщо складається рейтинговий список 20 студентів, то шкала буде містити Р20=20! списків. Від порядкової шкали можна перейти до шкали найменувань, виділивши за рейтинговим списком групу лідерів, що допоможе, наприклад, вибрати серед студентів вишу голову студентського самоврядування, або серед студентів однієї академічної групи старосту і його заступника. Очевидно, що з елементами розглянутої шкали рангів можна виконувати ті ж операції математичної логіки, що і з елементами номінальної шкали, а саме, визначення належності студента тій чи іншій рейтинговій групі та визначення кількості студентів в групі. Але розглянута шкала рангів має також і властивість порівняння всіх видів груп: студент (група), що має більш виражені лідерські якості, має вищий рейтинг. Зрозуміло, що елементи рейтингової шкали, виражені списком, не можна порівняти за ознакою «на скільки більший». Приклад 3. За допомогою комп’ютерного тестування досліджується властивість студента правильно виконати завдання. Номінальна шкала {виконано правильно, виконано неправильно} може бути замінена більш гнучкою шкалою, наприклад: {(правильно вибрано і пов’язано факти), (неправильно вибрано, але правильно пов’язано факти, або правильно вибрано, але неправильно пов’язано факти), (неправильно вибрано і неправильно пов’язано факти)}. Три значення цієї порядкової шкали природньо розташовані за рангами – вищому рангу відповідає уміння студента повністю правильно виконати завдання. Приклад 4. Яскравим прикладом шкали рангів є оцінювання успішності студентів за множиною {відмінно, добре, задовільно, незадовільно}або за шкалою ECTS {A, B, C,…}. Шкала інтервалів разом з властивостями попередніх видів шкал дає можливість оцінки видів досліджуваної властивості за рівними інтервалами і, відповідно, – можливість кількісно оцінити різницю видів (Рис. 2). Тут застосовуються майже всі статистичні методи, за винятком тих, в яких «нульова точка» однозначно відповідає відсутності даної властивості. Шкала інтервалів дозволяє суб’єктивним враженням ставити у відповідність числа зі значною частиною їх властивостей.
Рис. 2. Схематичне зображення шкали інтервалів (зліва) і шкали відношень (справа). Приклади шкали інтервалів. Приклад 1. Досліджується зацікавленість студента в освоєнні нової навчальної дисципліни. Шкала, що визначається дослідником, може мати такі значення (види, градації): «дуже цікаво», «цікаво», «в деякій мірі цікаво», «майже не цікаво», «не цікаво», «зовсім не цікаво». Відстань між сусідніми градаціями вважається однаковою. Приклад 2. Досліджується степінь згоди студента з поставленою йому оцінкою. В якості шкали дослідником обрано множину послідовних цілих чисел на числовій прямій, меншому з чисел якої ставиться у відповідність ознака «категорично не згоден», більшому – «повністю згоден». На думку окремих соціологів для оцінки привабливості професій випускники шкіл користуються інтервальною шкалою, хоча деякі соціологи привабливість професій виміряють в порядковій шкалі. Це підтверджує вказане означення шкали, в якому поділ на види залежить від дослідника. Шкала відношень вважається найбільш розповсюдженою в науці і практиці. Вона має всі властивості шкали інтервалів, до яких долучається ще наявність початку відліку – нульової точки, що дозволяє порівнювати значення видів досліджуваної властивості, використовуючи їх відношення або пропорції. Завдяки цьому шкала відношень не накладає ніяких обмежень на математичний апарат, що використовується для обробки результатів досліджень. Приклади застосування шкали відношень. Приклад 1. При дослідженні часу виконання студентом завдання в якості шкали природньо розглядати відрізок [0, tmax], де tmax – час, виділений на виконання завдання. Приклад 2. 100-бальну шкалу ECTS (без використання А, В, С,…) можна також вважати шкалою відношень. Використовуючи її, порівняння навчальних досягнень студентів може бути, наприклад, таким: «Один студент набрав балів у стільки-то разів більше, ніж інший». Таким чином, нами розглянуто основні види шкал, що використовуються в різних галузях людської діяльності; дано означення шкали досліджуваної властивості; наведено приклади застосування різних видів шкал. Це повинно спонукати студентів до отримання необхідних знань і понять щодо вимірів в професійних дослідженнях, отримання вмінь застосовувати їх, дозволить майбутнім спеціалістам з максимальною точністю і достовірністю аналізувати інформацію, ефективно та результативно застосовувати набуті знання та вміння в організації своєї професійної діяльності. Приклад застосування шкал у професії – менеджер по продажах сільгосптехніки. Шкала найменувань. Я розглядаю об’єкти: Т1, Т2, Т3, Т4, Т5, Т6, Т7, Т8, Т9, Т10, Т11, Т12 – одиниці сільгосптехніки, призначеної для продажу. Я виділяю в об’єктах таку ознаку: вид (тип, призначення) сільгосптехніки. За цією ознакою шкала найменувань містить види: сівалка, комбайн, трактор. Тоді розглядувані об’єкти можуть розподілятися по 3-х підмножинах, що не перетинаються:
З об’єктами, що «вимірюються» за шкалою найменувань, можна виконувати тільки операцію визначення приналежності – чи належать, наприклад, Т1 і Т6 одному виду, чи ні. З елементів математичної статистики для шкали найменувань використовується поняття наповненості (частоти) різних класів. Так, в даному прикладі, призначено для продажу: 4 сівалки, 3 комбайни, 5 тракторів. Порядкова шкала (шкала рангів). Я розглядаю ті ж самі об’єкти: Т1, Т2, Т3, Т4, Т5, Т6, Т7, Т8, Т9, Т10, Т11, Т12 – одиниці сільгосптехніки, призначеної для продажу. Тепер мене цікавить попит на них, оцінку якого я обераю за чотирма видами. Тоді об’єкти можуть розташуватися у порядку користування попитом так:
В ранговій шкалі разом з можливостями номінальної шкали є також можливість порівняння видів, тобто їх рангів. Так, в нашому прикладі, сівалка Т8 користується більшим попитом у споживачів, ніж трактор Т9. Тобто за даною шкалою Т8 має більш високий ранг, ніж Т9. Шкала інтервалів Я розглядаю ті ж самі об’єкти: Т1, Т2, Т3, Т4, Т5, Т6, Т7, Т8, Т9, Т10, Т11, Т12 – одиниці сільгосптехніки, призначеної для продажу. Мені важливо знати їх оцінку відвідувачами виставки Агро-Expo. Відвідувачам виставки пропонувалося відмітити своє враження від кожного виду техніки крапкою на відрізку:  І позиція ІІ позиція ІІІ позиція ІV позиція Зовсім не Є суттєві Немає суттєвих Дуже сподобалось зауваження зауважень сподобалось Тоді об’єкти можуть розташуватися, наприклад, у такому порядку:
Шкала інтервалів разом з властивостями попередніх видів шкал дає можливість оцінки видів досліджуваної властивості за рівними інтервалами і, відповідно, – можливість кількісно оцінити різницю видів. Наприклад, оцінка сівалки Т3 на 2 позиції менше оцінки комбайна Т1. Шкала інтервалів дозволяє суб’єктивним враженням ставити у відповідність числа зі значною частиною їх властивостей. Різниця шкали рангів і інтервалів: в шкалі інтервалів є сенс говорити «більше (менше) на стільки-то», а в шкалі рангів такого сенсу немає. Але в обох цих шкалах немає сенсу говорити «більше (менше) у стільки-то разів». Зато так можна говорити у шкалі відношень. Шкала відношень Я розглядаю ті ж самі об’єкти: Т1, Т2, Т3, Т4, Т5, Т6, Т7, Т8, Т9, Т10, Т11, Т12 – одиниці сільгосптехніки, призначеної для продажу. Мене цікавить їх собівартість (в умовних одиницях): Таблиця 1
Шкала відношень вважається найбільш розповсюдженою в практиці. Вона має всі властивості шкали інтервалів, до яких долучається ще можливість порівнювати значення видів досліджуваної властивості, використовуючи їх відношення або пропорції. Наприклад, собівартість одного виду у 3 рази більша за собівартість іншого. Наступна тема буде стосуватися операцій у шкалах відношень. Завдання контрольної роботи 11. Скласти і записати по одному прикладу на кожний з видів шкал зі своєї майбутньої професії. Тема: «ДИСКРЕТНІ СТАТИСТИЧНІ РЯДИ» Дискретним статистичним рядом називається перелік значень досліджуваної ознаки з відповідними частотами. Значення ознаки зазвичай беруться в зростаючому порядку. Приклад 1. Побудувати дискретний статистичний ряд собівартості сільгосптехніки з таблиці 1. Розв’зання. Позначимо xi собівартість техніки, ni частоту – кількість техніки з відповідною собівартістю. Тоді статистичний ряд матиме вид:
Основні числові характеристики статистичного ряду: середнє значення 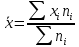 дисперсія 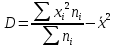 середнє квадратичне відхилення 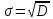 Приклад 2. Знайти основні числові характеристики статистичного ряду з прикладу 1. Розв’зання. Середнє значення 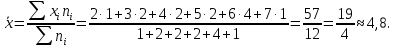 Дисперсія 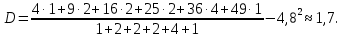 Середнє квадратичне відхилення 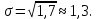 Завдання контрольної роботи 12. Побудувати дискретний статистичний ряд і знайти його основні числові характеристики за такими статистичними даними: 6, 7, 1, 3, 2, 4, 2, 3, 7, 2, 6, 5, 1, 1, 7, 6, 3, 5, 2, 1. |