Экзамен. Классификация и особенности применения По назначению и характеру выполняемых работ системы автоматики разделяют
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Основные системы автоматики. Их назначение. Отрасль техники и науки, которая объединяет теорию и методы проектирования системы автоматики, и устройств, способных выполнять свою основную работу без человека, называется автоматикой. Классификация и особенности применения По назначению и характеру выполняемых работ системы автоматики разделяют: Системы автоматического контроля служат для контроля некоторого процесса, и включают в себя датчик, усилитель, который принимает сигнал, элемент Р, реализующий последнюю операцию контроля – преобразование результата в удобной форме. Исполнительным элементом может выступать звуковой сигнал, любое другое сигнализирующее устройство (системы сигнализации). В автоматическую систему контроля входят распределители, блоки питания, стабилизаторы и другие компоненты. Независимо от числа компонентов такие системы разомкнутые, а сигнал идет в одном направлении: от контролируемого объекта Е к исполнительному компоненту Р. Системы автоматического управления служат для управления некоторым техпроцессом, используются для автоматизации процессов запуска, регулировки скорости вращения и реверса электромоторов в приводах механизмов. Одной из разновидности этой системы является система автоматической защиты. Она предотвращает наступление предельного и аварийного режимов, прекращая в необходимый момент работу. Системы автоматического регулирования удерживают регулируемый параметр в определенных пределах. Это является наиболее сложной автоматической системой, которая объединяет в себе управление и осуществление контроля. Одним из компонентов систем является регулятор. При выполнении этой системой всего одной задачи по поддержанию постоянного значения параметра, они называются системами стабилизации. Имеются процессы, нуждающиеся в изменении параметра по времени. Такие системы получили название систем программного регулирования. Виды систем автоматики. Система автоматического управления.  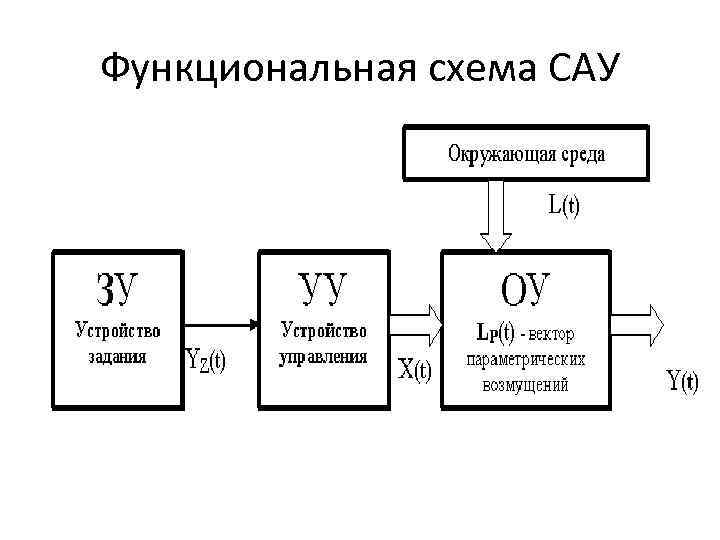 Пример про ТЭЦ,АЭС,ГЭС!!! Динамический режим работы звена. Динамическая характеристика. Динамической характеристикой звена называют зависимость выходной величины от входной в переходном процессе. Физическая задача определения выходной величины звена при изменяющемся входном сигнале сводится к решению дифференциального уравнения того или иного вида, описывающего протекание переходных процессов в звене. Дифференциальные уравнения движения динамического звена. В линейных системах автоматического регулирования протекающие процессы описываются линейными дифференциальными уравнениями, решение которых значительно упрощается с использованием методов операционного исчисления. Решение дифференциального уравнения методом операционного исчисления осуществляется в следующие три этапа; 1) переход от оригиналов к изображениям, т. е. переход от дифференциального уравнения к алгебраическому; отыскание из полученного алгебраического уравнения неизвестной функции Y (р), т. е. решение алгебраического уравнения; переход от найденного изображения Y (р) к оригиналу неизвестной функции. Дифференциальные уравнения движения звеньев имеют следующий вид: - безинерционное звено: - апериодическое - дифференцирующее: - интегрирующее: - колебательное: Передаточная функция. Передаточной функцией звена называется отношение изображения выходной величины звена к изображению входной величины при нулевых начальных условиях. Обозначим через W (р) передаточную функцию, а через X (р) и Y (р) - соответственно изображения входной и выходной величин, тогда: Переходная характеристика. Переходной характеристикой (переходным процессом) динамического звена называют зависимость выходной величины от времени при подаче на вход звена ступенчатого сигнала единичной амплитуды. Следовательно, переходная характеристика отображает реакцию звена на единичный ступенчатый сигнал. Частотные характеристики звеньев. Если на вход динамического звена поступает сигнал синусоидальной формы определенной частоты, то выходной сигнал имеет те же синусоидальную форму и частоту, но другие амплитуду и фазу. В связи с этим различают амплитудно-частотные и фазово-частотные характеристики звеньев. Амплитудно-частотная характеристика выражает отношение амплитуды колебаний на выходе звена к амплитуде колебаний на его входе в зависимости от частоты выходного сигнала (Рисунок 9, а) где Авых - амплитуда выходного сигнала; Авх - амплитуда входного сигнала; щ - угловая частота. 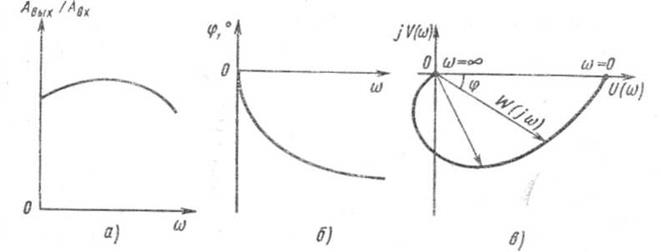 Рисунок 9 - Частотные характеристик звеньев: а- амплитудно-частотная; б - фазово-частотная; в - амплитудно-фазовая Фазово-частотная характеристика выражает зависимость разности фаз между входными и выходными колебаниями звена от частоты входного сигнала (Рисунок 9, б): Логарифмической амплитудно-частотной характеристикой (ЛАЧХ) L (щ) называют зависимость модуля частотной характеристики от частоты, представленную в логарифмическом масштабе. Логарифмической фазово-частотной характеристикой (ЛФЧХ) называют зависимость аргумента частотной характеристики от логарифма частоты. Статика элементов системы автоматического управления Различают два основных режима САУ: установивший (статический) режим работы, при котором составляющие вектора состояния системы не зависят от времени их измерения; динамический режим работы САУ, при котором составляющие вектора состояния системы являются некоторыми функциями времени. Одним из основных требований, предъявляемых к САУ, является обеспечение необходимой точности работы во всех режимах ее работы. В установившемся режиме работы САУ ее точностные характеристики могут быть определены по статической характеристике системы. Статическая характеристика называется аналитической, если функция Статическая характеристика называется неаналитической, если ее выходная величина или ее производные имеют разрывы непрерывности. 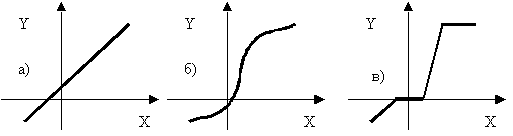 Рис. 1. Типы статических характеристик САУ На рис. 1 приведены линейная (а), нелинейная (б) и существенно нелинейная (в) статические характеристики САУ. Статическим (безинерционным) называется элемент, у которого при постоянном входном сигнале устанавливается с течением времени постоянное значение выходной координаты. Линейным статическим элементом называется безинерционный элемент, обладающий линейной статической характеристикой, уравнение которой имеет вид: Астатическим называется элемент, у которого при постоянном входном воздействии сигнал на выходе в установившемся режиме непрерывно растет с постоянной скоростью, ускорением и т. д. Для астатических элементов под уравнением статической характеристики следует понимать зависимость n-ной производной выходной величины от входной. Поскольку номер производной, принимающей постоянное значение различен, то для астатических элементов вводится понятие порядка астатизма. Одной из существенных характеристик САУ является зависимость между значением управляемого параметра и величиной внешнего воздействия на ОУ. По виду зависимости между значением управляемого воздействия и внешними возмущениями системы делят на статические и астатические. При установившихся режимах работы ошибка системы определяется как Динамика элементов системы автоматического управления Динамическими характеристиками элемента определяется его инерционность (время переходного процесса), изменение параметров элемента во время нагрузки, максимальное отклонение величины регулируемого параметра. К этим характеристикам относятся: - постоянная времени, - перерегулирование, - полоса пропускания. Элементы автоматики также могут подразделяться на инерционные и безынерционные. Примерами безынерционных элементов могут служить жесткие связи, передающие величины физических параметров без задержек по времени, т.е. переходной процесс к установившемуся состоянию отсутствует. Инерционные элементы – такие элементы, у которых переходной процесс от одного установившегося состояния к другому установившемуся состоянию имеет место. Классификация САУ по классам дифференциального управления По классам дифференциальных ура в н е н и й, которыми они описываются, различают САУ, приведенные на рис. 1.8. Линейными называют системы, которые могут быть отражены линейными операторными уравнениями (например, линейными дифференциальными уравнениями или системами этих уравнений); в противном случае система входит в класс нелинейных. Линейные и нелинейные дискретные системы характеризуются соответственно линейными и нелинейными разностными уравнениями или их системами. Линейные и нелинейные стационарные системы выражают дифференциальные уравнения или системы уравнений с постоянными коэффициентами. Линейные и нелинейные нестационарные системы описываются дифференциальными уравнениями или системами уравнений с переменными коэффициентами. Сосредоточенные системы, или системы с сосредоточенными параметрами, определяются обыкновенными дифференциальными уравнениями. Распределенные системы, или системы с распределенными параметрами, описываются дифференциальными уравнениями в частных производных. Понятия о случайных величинах. Законы распределения случайной величины. Определение 1. Случайнойназывается величина, которая в результате испытания принимает только одно значение из возможного множества своих значений, наперед неизвестное и зависящее от случайных причин. Различают два вида случайных величин: дискретные и непрерывные. Определение 2. Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное. Другими словами, возможные значения дискретной случайной величину можно перенумеровать. Описать случайную величину можно с помощью ее закона распределения. Определение 3. Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями. Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят ломаную, соединяющую последовательно точки с координатами (xi;pi), i=1,2,…n. Полученную линию называют многоугольником распределения (рис. 4.1). 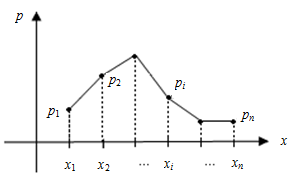 Рис. 4.1 Закон распределения дискретной случайной величины Х может быть также задан аналитически (в виде формулы): P(X=xi)=φ(xi),i =1,2,3…n. Понятия о случайных процессах. Характеристики случайных процессов. Случайным процессом называется множество или семейство случайных величин, значения которых индексируются временным параметром. Например, число студентов в аудитории, атмосферное давление или температура в этой аудитории как функции времени являются случайными процессами. Случайные процессы находят широкое применение при изучении сложных стохастических систем как адекватные математические модели процесса функционирования таких систем. Основными понятиями для случайных процессов являются понятия состояния процесса и перехода его из одного состояния в другое. Значения переменных, которые описывают случайный процесс, в данный момент времени называются состоянием случайного процесса. Случайный процесс совершает переход из одного состояния в другое, если значения переменных, задающих одно состояние, изменяются на значения, которые определяют другое состояние. Число возможных состояний (пространство состояний) случайного процесса может быть конечным или бесконечным. Если число возможных состояний конечно или счетно (всем возможным состояниям могут быть присвоены порядковые номера), то случайный процесс называется процессом с дискретными состояниями. Например, число покупателей в магазине, число клиентов в банке в течение дня описываются случайными процессами с дискретными состояниями. Математическая модель САУ. Преобразование структурных схем. Элементы САУ, математические модели которых описываются в виде передаточных функций, могут быть соединены последовательно, параллельно и с обратной связью. Рассмотрим записи эквивалентных передаточных функций при указанных типах соединений. 1. При параллельном соединении элементов на вход элементов и подается один и тот же сигнал . Эквивалентная передаточная функция параллельного соединения элементов и будет равна сумме передаточных функций и . 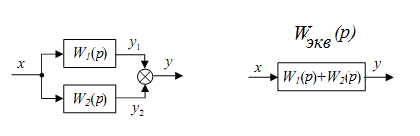 Рисунок 4.1. Параллельное соединение элементов 2. При последовательном соединении элементов и выходной сигнал первого элемента будет равен входному сигналу второго элемента, а эквивалентная передаточная функция будет равна произведению передаточных функций и . 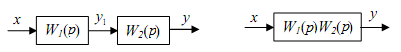 Рисунок 4.2. Последовательное соединение элементов 3. При соединении элементов с отрицательной обратной связью: 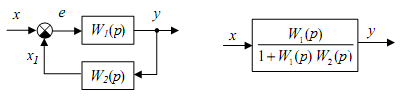 Рисунок 4.3. Соединение элементов с отрицательной обратной связью 4. При соединении с положительной обратной связью: 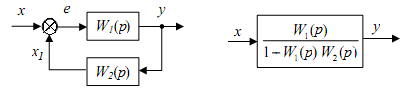 Рисунок 4.4. Соединение элементов с отрицательной обратной связью 5. Звено можно переносить через сумматор как вперед, так и назад. Чтобы при этом передаточные функции не изменились, перед сумматором нужно поставить дополнительное звено: 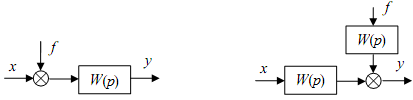 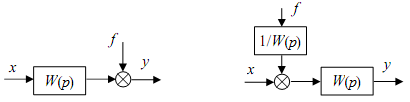 Рисунок 4.5. Перенос через сумматор 6. Звено можно переносить также через точку разветвления, сохраняя все передаточные функции: 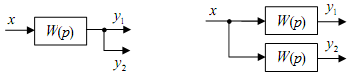 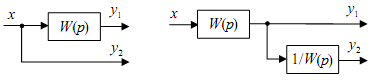 Рисунок 4.6. Перенос через точку разветвления Статический режим работы звена. Статическая характеристика. Поведение САУ как в динамике, так и в статике определяется поведением составляющих их звеньев. Звено автоматического устройства – это условно выделенная часть его, функционирующая по определенному алгоритму. Звенья САУ взаимодействуют по средствам связи. Связь – это условно выделенная часть системы, автоматически отражающая направление взаимодействия между звеньями, т.о. любая САУ может быть представлена в виде звеньев и связей между ними, такая схема системы называется структурной схемой. Точка приложения входной координаты - входом звена, а выходной – выходом. Функциональная зависимость – установившихся значений входных и выходных координат называется статической характеристикой звена. Y1=f(x1); Y2=f(x2) – статическая характеристика второго звена. По виду статической характеристики все звенья делятся на статические и астатические, линейные и нелинейные. Статические звенья – это звенья, у которых функциональная связь между входной и выходной координатами в рабочей области непрерывная и монотонная, т.е. каждому значению x отвечает единственное значение y. Если при этом статическая характеристика линейная или достаточно точно может быть аппроксимирована прямой, то такое статическое звено – линейное. При криволинейности статической характеристики или наличии в ней кусочно-линейных участков, статическое звено - нелинейное. Астатические звенья – звенья, у которых при отсутствии функциональной связи между входной и выходной координатами в статическом режиме имеется функциональная связь между входной координатой и изменениями выходной координаты. Порядок производной функциональной зависимости определяет порядок астатизма звена. Выходными координатами звена могут быть разные физические величины, которые влияют на порядок астатизма звена Виды динамических характеристик. Область применения. Перемещение спортсмена в пространстве и во времени, выполнение практически всех телесно-двигательных упражнений на снарядах и со снарядами является результатом взаимодействия внешних и внутренних сил. В результате действия и взаимодействия различных сил характер перемещения постоянно изменяется по величине и направлению. Такие изменения лежат в основе механизмов двигательных действий, что составляет сущность целостного упражнения. Познать эти механизмы позволяют динамические характеристики. Группа динамических характеристик подразделяется на три подгруппы: инерционные, позволяющие изучать особенности перемещения тела исполнителя и звеньев, которые он приводит в движение; силовые, которые применяются для познания особенностей взаимодействия частей и звеньев тела человека как биомеханической системы и ее взаимодействия с внешними телами; энергетические, посредством которых представляется возможным изучать особенности энергообеспечения работы человека как биомеханической системы, обмена энергией между нею и средой. Надо иметь в виду то обстоятельство, что энергетические характеристики определяются только путем измерений с применением расчетных и инструментальных методов. Потому, эта группа характеристик носит ограниченный характер в процессе качественного биомеханического анализа телесно-двигательных упражнений. Тем не менее знание сущности каждой динамической характеристики позволяет на логическом уровне рассуждать о механизмах двигательных действий, причинах их проявления, изменениях, строить умозаключения и в доступных пределах познавать телесно-двигательное упражнение. Инерционные характеристики отражают особенности самого движущегося тела и других, взаимодействующих с ним тел, оказывают прямое влияние на изменение и сохранение скорости точки или тела. В эту группу характеристик входят инертность, масса тела, момент инерции тела. Под инерцией понимается свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения. Примером может быть движение космического корабля в открытом космосе, где его скорость неизменна и равна той, которая была придана кораблю двигателем последней ступени ракеты - носителя. Типовое элементарное звено. Работа звена. Характеристики звеньев. САУ состоят из отдельных блоков (устройств, узлов), каждый из которых, включая и объект управления, получает на входе информацию, преобразует и передает со своего выхода на вход следующего блока. Хвх Х вых Помимо передачи сигналов блоки оказывают друг на друга и энергетическое воздействие. Чтобы понять, каким образом данный блок будет реагировать на разнообразные сигналы, его представляют в виде последовательного или параллельного (реже) соединения нескольких элементарных звеньев. Разбиение структуры на звенья делается так, что все звенья являются направленными. Звено должно влиять только на свой выход, но не на вход. Для каждого звена существует определённый диапазон входного сигнала, в пределах которого оно способно функционировать. Это рабочий диапазон звена. Характеристики звеньев разнообразны (линейные, не линейные; статические, динамические; устойчивые, не устойчивые). В большинстве случаев - устойчивые статические звенья. Основное свойство таких звеньев состоит в том, что по прошествии некоторого интервала времени после установления входного сигнала на постоянном уровне выходной сигнал тоже становится постоянным. K [ x(∞)]= у(∞)/x(∞) – коэффициент передачи или преобразование звена ( может быть размерным и безразмерным). Х и У могут быть электрическими (I;R;C;B) и не неэлектрическими (температура, давление, скорость, ускорение, расход жидкости и т.д.) k – зависит от величины входного сигнала. Если зависимость мала, то звенья называют линейными статическими. Не линейность звена может носить разнообразный характер и её можно оценить по характеристике звена. Пропорциональное звено. Уравнение взаимосвязи входного и выходного сигнала пропорционального звена является алгебраическим. Это означает, что оно может служить операторной формой записи уравнения звена: Передаточная функция пропорционального звена имеет вид: 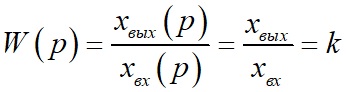 АФХ пропорционального звена не зависит от частоты ω, поэтому годограф ее вектора (рисунок ниже а)) превращается в точку С, которая находится на положительной действительной полуоси комплексной плоскости на расстоянии k от начала координат. 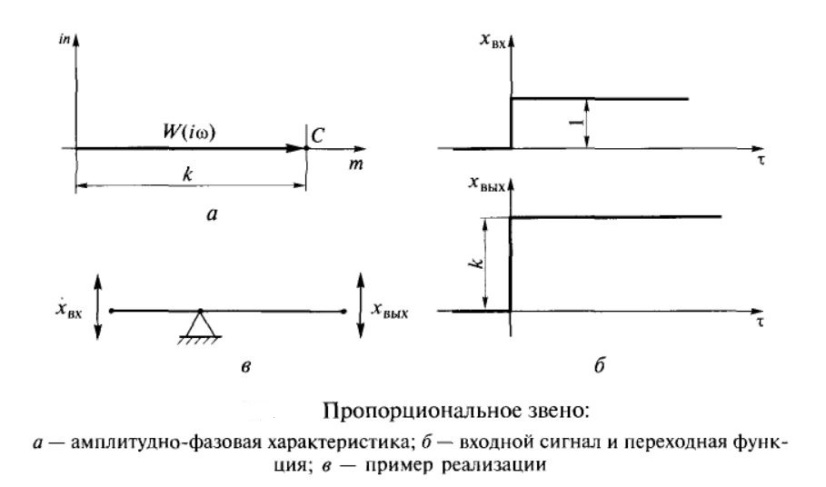 Реакция на возмущающее воздействие у пропорционального звена происходит мгновенно (инерция отсутствует). График переходной функции (рисунок б)) показывает, что выходной сигнал звена пропорционален входному. Разница между входным и выходным сигналом регламентируется величиной коэффициента усиления сигнала k. Физическим примером безынерционного звена может послужить жесткий стержень (рисунок в)), лежащий на опоре, при перемещении одного из концов которого (Хвх) – мгновенно переместится и второй конец (Хвых). Еще одним примером может послужить резистор – при подаче напряжения, ток через резистор потечет мгновенно, без задержек (в отличии от RL или RC цепей). Интегрирующее и апериодическое звенья. |
