Экзамен. Классификация и особенности применения По назначению и характеру выполняемых работ системы автоматики разделяют

• Название: Классификация и особенности применения По назначению и характеру выполняемых работ системы автоматики разделяют
• Дата: 01.02.2022
• Размер: 1.08 Mb.
• Имя файла: Экзамен.docx
• Тип: Документы; #348438
• страница: 2 из 9

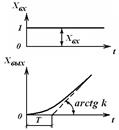
Апериодическое звено.

Апериодическим звеном называется простейший динамический элемент системы автоматического управления или его составная часть, имеющая передаточную функцию вида

(1)

на структурных схемах апериодическое звено изображается следующим образом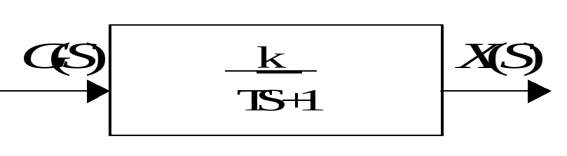



Динамические свойства апериодического звена определяются двумя параметрами:

- коэффициент усиления (коэффициент передачи) апериодического звена;

• 
  - постоянная времени апериодического звена.
  

Интегрирующее звено. Это звено, у которого скорость изменения выходной величины пропорциональна входной величине.

Уравнение идеального интегрирующего звена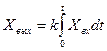

. (3.33)

Уравнение интегрирующего звена с учетом инерционных свойств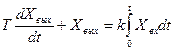

. (3.34)

Переходная характеристика интегрирующего звена представлена на рис. 3.17.

 


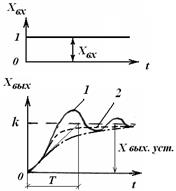
Рис. 3.17. Переходная характеристика интегрирующего звена

Передаточные функции:

– идеального звена ; (3.35)

– звена с инерцией , (3.36) где k - угловой коэффициент наклона касательной к оси абсцисс.

Примерами интегрирующего звена являются: поршневой ИМ, у которого входная величина – перемещение плунжера золотникового устройства, а выходная – перемещение силового поршня; маломощный асинхронный двигатель с полым ротором; контур R – C, если и др.

Колебательное и дифференцирующее звенья.

Колебательное звено. Колебательным называется звено, в котором при подаче на вход ступенчатого воздействия выходная величина стремится к установившемуся значению, совершая затухающие колебания.

Колебательное звено иначе называют двухъемкостным, т.е. оно должно содержать два элемента, способных запасать энергию или вещество и обмениваться этими запасами через третий элемент.

Дифференциальное уравнение колебательного звена:

(3.21)

или в операторной форме

, (3.22)

где – постоянная времени, характеризующая демпфирование (затухание) собственных колебаний звена; – постоянная времени, характеризующая раскачивание собственных колебаний звена; – коэффициент усиления.

Переходная характеристика колебательного звена представлена на рис. 3.14.

Следует иметь в виду, что не всякое уравнение второго порядка (3.21) выражает колебательный процесс.

Если , то практически будет иметь место апериодический процесс (кривая 2). При таких параметрах и динамическое звено называют апериодическим звеном второго порядка.

Если , то будет иметь место колебательный процесс (кривая 1). Чем меньше отношение , тем сильнее проявляются колебания.

Решение дифференциального уравнения для колебательного звена: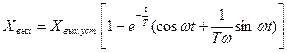

, (3.23)

где – постоянная времени, характеризующая длительность переходного процесса.

Величина может быть определена графически по кривой (рис. 3.14), как постоянная времени огибающей экспоненты.

 

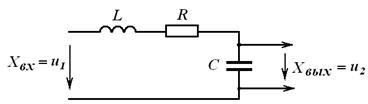
Рис. 3.14. Переходная характеристика колебательного звена

 

Аналитически величину можно определить по формуле

; . (3.24)

Постоянные времени и часто определяют по параметрам элементов колебательного звена.

Частота собственных колебаний звена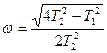

. (3.25)

Передаточная функция колебательного звена

. (3.26)

К колебательным звеньям относятся:

– электрическая цепь с последовательным соединением R, L и C;

– сообщающиеся сосуды;

– электродвигатели, способные запасать кинетическую энергию в якоре и электромагнитную в якорной цепи;

– механические элементы, обладающие массой, упругостью и вязким трением и др.

Например, для электрической цепи с последовательным соединением параметров R, L и C (рис. 3.15), постоянные времени и можно определить по формулам:


. (3.27)

 

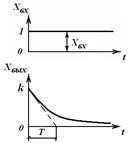
Рис. 3.15. Электрическая цепь с последовательным

соединением параметров R, L и C

 

Дифференцирующее звено. Это звено, у которого выходная величина пропорциональна скорости изменения входной величины. Как всякое реальное звено, дифференцирующее звено имеет инерционные свойства.

Дифференциальное уравнение звена (реального):

. (3.28)

Его решение

, (3.29)

где – постоянная времени звена; – коэффициент передачи.

Переходный процесс в дифференцирующем звене представлен на рис. 3.16.

Если инерционные свойства звена незначительны в сравнении с другими звеньями САР, то величину опускают и получают уравнение идеального дифференцирующего звена

. (3.30)

Передаточная функция реального звена:

, (3.31)

а идеального звена

. (3.32)

К дифференцирующим звеньям относятся: тахогенератор (датчик скорости), у которого – угол поворота вала, а – напряжение; пневматические и гидравлические успокоители; дифференцирующий трансформатор; цепь, состоящая из элементов R и C.

Дифференцирующие звенья находят широкое применение как составные элементы корректирующих устройств САР.