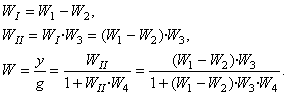Экзамен. Классификация и особенности применения По назначению и характеру выполняемых работ системы автоматики разделяют
 Скачать 1.08 Mb. Скачать 1.08 Mb.
|
|
Рис. 3.16. Переходная характеристика дифференцирующего звена Частотные характеристики систем. Представление в виде произведения и в векторной форме. Частотные характеристики САУ характеризуют реакцию систем на синусоидальное входное воздействие в установившемся режиме. К частотным характеристикам относятся: АФЧХ - амплитудно-фазовая частотная характеристика; АЧХ - амплитудно-частотная характеристика; ФЧХ - фазовая частотная характеристика; ЛАЧХ - логарифмическая АЧХ; ЛФЧХ - логарифмическая ФЧХ. АФЧХ представляет собой частотную передаточную функцию W(jω), которая получается путем замены в передаточной функции W(p) оператора Лапласа p на комплексную переменную jω. АФЧХ представляет собой вектор на комплексной плоскости в полярных координатах Н(ω) и φ(ω), которые являются соответственно АЧХ и ФЧХ: Частотная передаточная функция – отношение изображений Фурье выходного и входного сигналов. 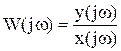 , , 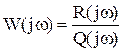 где Для линейных устойчивых систем при нулевых начальных условиях возможен взаимный однозначный переход между передаточными функциями систем в непрерывном времени. Для таких процессов преобразование Лапласа переходит в преобразование Фурье, если произвести подстановку s = jw. Частотная ПФ связана с частотными характеристиками следующим образом: Частотная передаточная функция 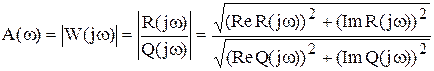 ; (10.4) ; (10.4)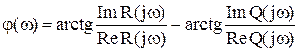 Частотную передаточную функцию можно представить в алгебраической форме: W(jω) = U(ω) + jV(ω) = ReW(jω) + jImW(jω). Взаимосвязь между различными формами представления W(jω): 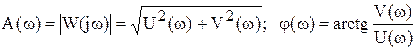 ; ;U(ω) и V(ω) можно получить непосредственно из W(jω). Для этого необходимо представить частотную ПФ в следующем виде: 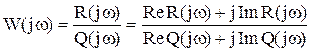 . .Затем умножить числитель и знаменатель на выражение комплексно сопряженное знаменателю. Затем выделить действительную и мнимую части. Пример: получение частотной передаточной функции из передаточной функции в форме изображений по Лапласу для статического апериодического инерционного звена 1-го порядка. W(s) = Общая форма частотной ПФ получается формальной заменой оператора s на 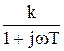 . .Чтоб перейти к алгебраической форме помножим числитель и знаменатель на выражение комплексно-сопряженное знаменателю 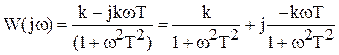 Вывести частотные ПФ самостоятельно для всех звеньев. Итак, частотные характеристики можно построить различными способами: 1. Можно аналитически получить частотную передаточную функцию звена (системы), а затем промоделировать выражения (10.4). 2. Можно подавать на вход звена (системы) гармонические входные воздействия с различной частотой и вычислять АЧХ и ФЧХ по формулам (10.1), (10.2). Эти два метода являются достаточно трудоемкими, особенно когда речь идет о построении частотных характеристик сложных систем. 3. Можно воспользоваться средствами компьютерного моделирования. Специальный блок, разработанный в Simulink – «Анализатор частотных характеристик» производит построение АЧХ, ФЧХ и АФЧХ звена или системы. Рассмотрим, как работает блок и как проводить компьютерные эксперименты по снятию частотных характеристик звена (системы). Типы соединения звеньев систем.
Обратная связь. Цепи с обратной связью. В большинстве цепей с зависимыми источниками имеется по крайней мере два пути прохождения сигнала: прямой (от входа к выходу) и обратный (с выхода на вход). Обратный путь прохождения сигнала реализуется с помощью специальной цепи обратной связи (ОС). Таких путей, а значит, и цепей ОС может быть несколько. Наличие в цепях с зависимыми источниками ОС придает им новые ценные качества, которыми не обладают цепи без ОС. Например, с помощью цепей ОС можно осуществить температурную стабилизацию режима работы цепи, уменьшить нелинейные искажения, возникающие в цепях с нелинейными элементами, улучшить технические параметры усилителей и т. д. Введение ОС позволяет создавать цепи, генерирующие колебания различной формы, моделирующие различные функции (суммирование, интегрирование, дифференцирование и др.). Кроме положительных, ОС могут оказывать и отрицательные последствия на цепь. Так, ОС могут образовываться за счет различных "паразитных" связей, возникающих в результате неудачного монтажа элементов цепи или при нерациональном формировании элементов в подложке микросхемы и др. Подобные ОС могут возникать на высоких частотах за счет различных "паразитных" емкостей создающих цепи обратной связи с выхода на вход. "Паразитные" ОС могут оказывать неконтролируемые воздействия на работу цепи и поэтому должны учитываться в необходимых случаях при расчетах. Все вышеизложенное свидетельствует о важности изучения цепей с ОС. Обратные связи могут быть классифицированы по различных признакам: по характеру связи – положительной (ПОС), отрицательной (ООС) и комплексной; по структуре – внешней и внутренней; по характеру реализующих ее элементов – активной и пассивной, линейной и нелинейной, частотно зависимой и частотно независимой и т. д. С точки зрения анализа важным являются способы соединения четырехполюсников прямой передачи и цепи ОС. На рис. 14.1 представлены основные схемы соединения четырехполюсника каналов прямого усиления с передаточной функцией Hу(p) и четырехполюсника цепи ОС с передаточной функцией Hос(p). Причем, в качестве четырехполюсника с Hу(p) обычно используют активные цепи (усилитель), а в качестве цепи ОС с передаточной функцией Hос(p) пассивный четырехполюсник. В дальнейшем ограничимся случаем, когда усилитель и цепь ОС являются линейными четырехполюсниками. 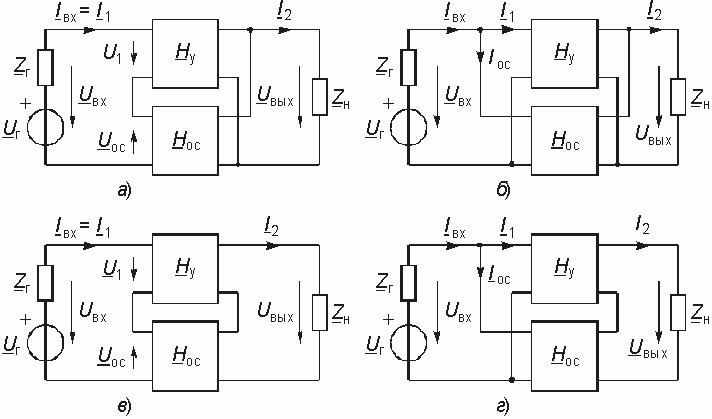 Данные схемы соответствуют последовательно-параллельному (а), параллельному (б), последовательному (в) и параллельно-последовательному (г) соединению четырехполюсников. В соответствии с этим для анализа подобных сложных четырехполюсников могут использоваться H, Y, Z, F-параметры соответственно, поэтому в литературе иногда эти структуры называют ОС H, Y, Z и F-типа соответственно. В соответствии со структурными схемами (рис. 14.1) различают следующие виды ОС: последовательной по напряжению (рис. 14.1, а), т. к. Uос зависит от Uвых; параллельной по напряжению (рис. 14.1, б), поскольку ток Iос является функцией выходного напряжения U2; последовательной по току (рис. 14.1, в), т. к. Uос в этой схеме зависит от выходного тока I2; параллельной по току (рис. 14.1, г), потому что Iос будет зависеть от выходного тока I2. Для определения типа ОС (по току или напряжению) необходимо помнить, что ОС по напряжению будет максимальной при ХХ на выходе и минимальной при КЗ на выходе, а ОС по току будет максимальной при КЗ на выходе и минимальной (равной нулю) при ХХ на выходе. Объекты регулирования и их свойства Объект регулирования является элементом АСР, и свойства всей системы во многом определяются свойствами объекта. Изучение свойств объектов регулирования — важный и часто основной этап разработки АСР. Объект регулирования в отличие от остальных элементов АСР является заранее заданным элементом, свойства которого определяются его значением в технологическом процессе. Поэтому создание АСР сводится к подбору остальных элементов с такими свойствами, чтобы свойства всей системы обеспечивали требуемую точность стабилизации регулируемого параметра, что невозможно сделать без знания свойств объекта. С позиций теории регулирования объект рассматривают как устройство, преобразующее по определенному закону свои входные сигналы в выходные. Состояние объекта в каждый момент времени определяется его выходными сигналами (регулируемыми параметрами), зависимость которых от входных (т. е. характер преобразования сигналов) и обусловливает свойства объекта. Другие свойства объектов, характеризующие их физическую природу, конструкцию, условия эксплуатации, находящуюся в них среду и т. п., как указывалось, несущественны для процессов регулирования. Поэтому часто самым различным по своей природе объектам присущи одинаковые зависимости выходных сигналов от входных. При управлении инженерными системами их разбивают на элементарные объекты регулирования, как правило, с одним регулируемым и одним регулирующим параметрами. Управление такими объектами осуществляется одноконтурными АСР. Поэтому здесь будут рассматриваться свойства только объектов регулирования с одним выходным сигналом. Принято различать статические и динамические свойства объектов регулирования. Статические свойства объекта — это его свойства в установившемся состоянии (в статике), т. е. при неиз-меняющихся входном и выходном сигналах. При этом зависимость установившегося значения выходного сигнала от входного называется статической характеристикой объекта. | ||||||

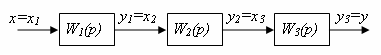
 . (2)
. (2)
 (3)
(3) (4)
(4) (5)
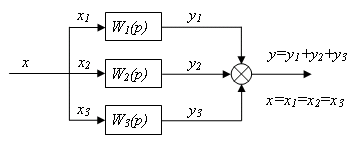
(5)
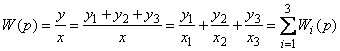 .
.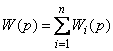 . (1)
. (1)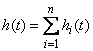 , (2)
, (2)