Одна схема передачи на основе переменного модулятора MSK для обе. Ключевые слова безопасность физического уровня беспроводная связь

• Название: Ключевые слова безопасность физического уровня беспроводная связь
• Дата: 06.04.2023
• Размер: 391.87 Kb.
• Имя файла: Одна схема передачи на основе переменного модулятора MSK для обе.docx
• Тип: Документы; #1041404

Одна схема передачи на основе переменного модулятора MSK для обеспечения безопасности беспроводного физического уровня беспроводной сети

Гоччжэнь Цзан, Баохуа Хуан, Лихуа Чэнь, Юаньюань Гао

Колледж коммуникационной инженерии, Университет науки и технологии НОАК, Нанкин, Китай, [e-mail]

Аннотация — В данной работе исследуются методы генерации сигнала MSK (минимальное смещение ключа) и представлены 8 типов структур MSK modulator. Результаты показывают, что структура модулятора MSK имеет определенную функцию шифрования формы сигнала для входных сообщений. Основываясь на этом открытии и идее частотно-хоппинговой связи, мы предлагаем схему передачи физического уровня с модуляцией MSK, где структура модулятора MSK может быть изменена в соответствии с секретом между источником и пунктом назначения. С помощью теоретического анализа и экспериментального моделирования мы показываем, что BER (битовая частота ошибок) достигает около 50%, что делает демодированиепрактически невозможным для подслушивающего устройства в предлагаемой схеме, тем самым обеспечивая связь между источником и пунктом назначения. Кроме того, эта схема передачи безопасности не зависит от вариаций канала беспроводной средыи очень подходит для беспроводных сетей, где канал остается статическим в течение большей части срока службы сети.

Ключевые слова — безопасность физического уровня; беспроводная связь;

Модуляция MSK

I. ИНТРОДУКЦИЯ

Беспроводная связь особенно уязвима для атак безопасности из-за присущей среде передачи открытости. В последнее время безопасность физического уровня привлекает все большее внимание [1-8]. Общий подход к повышению безопасности нафизическом уровне заключается в том, чтобы полагаться на вариации каналов беспроводной среды. Хотя этот тип подход не всегда подходит для беспроводных сетей, где канал остается статическим в течение большей части срока службы сети [8]. Для этих сценариев более подходящим является независимый метод безопасности физического уровня, который будет полагаться на секрет, известный источнику и месту назначения, но не подслушивающему устройству. В последнее время для беспроводной связи было исследовано несколько подходов к обработке сигналов для повышения безопасности передачи информации на физическом уровне [6-8]. Метод безопасности физического уровня, который использует разнообразие созвездий QAM (квадратурной амплитудной модуляции) в беспроводных сетях, предложен в [8], который не зависитот характеристик канала и может обеспечить секретность Шеннона, а любая атака методом перебора со стороны подслушивающего устройства влечет за собой высокие накладные расходы и ничтожную вероятность успеха.

Модуляция MSK была хорошо изучена и широко примененак беспроводной связи , поскольку она имеет некоторые явные преимущества, такие как постоянная амплитуда, высокая эффективность полосы пропускания, небольшая внеполосная мощность и т.д . В данной работе изучены модифицированные методы генерации сигнала MSK и представлены 8 типов MSK модуляторных структур (включая основную квадратурную структуру). А затем, ссылаясь на идею частотно-скачкообразной коммуникации, предлагается новая схема передачи физического уровня на основе модуляции MSK, где структура модулятора MSK может быть изменена в соответствии с секретом между источником и пунктом назначения. Благодаря теоретическому анализу и экспериментальному моделированию мы можем обнаружить, что BER (битовая частота ошибок) на подслушивающем устройстве всегда достигает около 50% в предлагаемой схеме, что эквивалентно случайному угадыванию с демодуляционной целью и делает подслушивание демодуляции практически невозможным, тем самым обеспечивая связь между источником и пунктом назначения. Более того, новая схема не может принести повышенной сложности.

Остальная часть настоящего документа организована следующим образом. В разделе II представлены 8 видов метода генерации сигналаMSK, а затем анализируется функция шифрования структуры модулятора MSK для входных сообщений. В разделе III представлена новая схема передачи, основанная на переменном модуляторе MSK для обеспечения безопасности физического уровня. А теоретический анализ и моделирование ltsпредставлены в разделе IV. Наконец, в разделе V кратко излагается наша работа.

См. GENERATING METHODS МСК СИГНАЛ

MSK является особой формой двоичной непрерывно-фазовой модуляции 2FSK с индексом модуляции h = 0,5 и имеет квадратурное выражение для символа kth (k ≥ 1) как s _MSK(t)=I_kAcos2πf_dtcos2πf_c t-Q_kAsin2πf_dtsin2πf_ct, (k-1)T _b≤t≤kT_b (1)

Эта работа была поддержана Национальным научным фондом Китая в рамках грантового 61201242 и Фондом предварительных исследований PLA UST. 978-1-4673-7687-7/15/$31.00 ©2015 IEEE

где A — амплитуда сигнала, T_b — ширина символа, f_d = 1/(4T_b), f_c = m/(4T_b) — модулированная несущая частота, m —

положительное целое число. Cos2πf_dt и sin2πf_dt называются весовыми функциями внутрифазной и квадратурной составляющих S_MSK(t) соответственно. I_k = cosφ_k и Q_k = a_kcosφ_k называются эквивалентными данными, соответственно. А k = ±1 — k-е входное сообщение; φ_k - это фазовое состояние сигнала, которое приводит к непрерывности фаз между соседними интервалами. С помощью некоторых тригонометрических преобразований (1) показывает, что форма сигнала MSK является

синусоида, имеющая одну из двухвозможных e частот f₁ = f_c + f_d и f₂ = f_c − f_d в интервале (k-1)T_b ≤ t ≤ kT_b.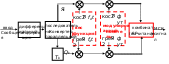

Рисунок 1. Принципиальная блок-схема модулятора MSK

Согласно возможному значению_k и φ_k в (1), принципиальную блок-схему модулятора MSK можно получить на фиг.1, что часто встречается в некоторых литературах, таких как [9-11]. На практике возникают некоторые проблемы при реализации блок-схемы. Обратите внимание, что на рисунке 1, после задержки сигнала ветви Q T_b, интервалы символов {I_k} и {Q_k} равны 2iT_b

(2i+2)T_b и (2i+1)T_b(2i+3)T_b, соответственно, где целое число i ≥ 0. В то время как в (1) k-й интервал символа равен (k-1)T_b kT_b, а возможное время перехода полярности равно t = kT_b = (2i+1)T_b для {I_k}, и t = kT_b = 2iT _b для {Q_k}, то символьные интервалы {I_k} и {Q_k} равны (2i−1)T_b (2i+1)T_b и 2iT_b (2i+2)T_b соответственно. Во время этих интервалов символов вес functions cos2πf_dt и sin2πf_dt встречается: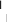

cos2πf td t= −(2 1) (2 1)i Tb i+ Tb = sin2πf td t=2 (2 2)iTb i+ Tb , и sin2πf td t=2iTb(2 2) i+ Tb = −_cos2πf td t_{= +}(2 1) (2 3)i Tb i₊ Tb , которые являются полупериодом синусоидального импульса. Таким образом, фактические весовые функции в модуляторе MSK на рис.1 должны быть sin2πf_dt и −cos2πf_dt для I и Q ветвей соответственно. Более того, во время двух смежных символов интервала 4T_b, форма импульса представляет собой одну полнопериодическую форму волны sin2πf_dt (полярность не учитывается). Для простоты в фактической схеме sin2πf_dt и cos2πf_dt часто используются в качестве весовых функций для ветви I и Q соответственно, а затем сумматор используется в качестве комбайнера. Если в качестве единицы измерения используется T b, то соответствующий выходной сигнал может быть выражен как s_MSK(t)=I_nAsin2πf_dtcos2πf_ct+Q_nAcos2π ф_дтсин2πф_кт, н≥1 (2)

где, In = [u1 u1 u3 u3 u5 u5... у2и-1 у2и-1... ], Qn = [u0 u2 u2 u4 u4 u₆ u₆... у_2и у_2и... ], и {u_n = +1 или −1, n ≥ 1} — биполярный дифференциальный код входного сообщения {a_n}, а ширина его символа — T_b. u₀ = +1 или −1, является начальным значением Q_n. Здесь для символа nth (n ≥ 1) интервал равен (n−1)T_b ≤ t ≤ nT_b. Поскольку модулятор MSK на рис.1 может быть получен непосредственно по выражению сигнала MSK, мы называем его основным модулятором MSK. На самом деле, если некоторые части модулятора, такие как весовая функция, модулированный носитель и комбанер, будут модифицированы просто, будет 7 типов модифицированной структуры модулятора MSK. Подробности можно увидеть в ТАБЛИЦЕ I, а базовый модулятор MSK является первым типом. Теоретически можно доказать, что выходные сигналы этих модифицированных модуляторов в ТАБЛИЦЕ I являются сигналами MSK. Доказательство не представлено в этой статье с учетом ограничений по страницам.

ТАБЛИЦА I. ТХЕ ГENERATING METHODS МСК СИГНАЛ

Метод генерации	Выражение выходного сигнала	Замечание
1-й тип	sMSK(t)=InAsin2πfdtcos2πfct+QnAcos2πfdtsin2πfct	In = [u1 u1 u3 u3 u5 u5... у2и+1
2-й тип	sMSK(t)=InAsin2πfdtcos2πfct−QnAcos2πfdtsin2πfct	u2i+1... ], Qn = [u0 u2 u2 u4 u4 u6 u6... у2и у2и ... ], где {un = +1 или −1, n ≥ 1} — биполярное расстройство дифференциальный код {an}, и u0 = +1 или −1, — начальное значение Qn.
3-й тип	sMSK(t)=InAsin2πfdtsin2πfct+QnAcos2πfdtcos2πfct
4-й тип	sMSK(t)=InAsin2πfdtsin2πfct−QnAcos2πfdtcos2πfct
5-й тип	sMSK(t)=InA|sin2πfdt|cos2πfct+QnA|cos2πfdt|sin2πfct
6-й тип	sMSK(t)=InA|sin2πfdt|cos2πfct−QnA|cos2πfdt|sin2πfct
7-й тип	sMSK(t)=InA|sin2πfdt|sin2πfct+QnA|cos2πfdt|cos2πfct
8-й тип	sMSK(t)=InA|sin2πfdt|sin2πfct−QnA|cos2πfdt|cos2πfct

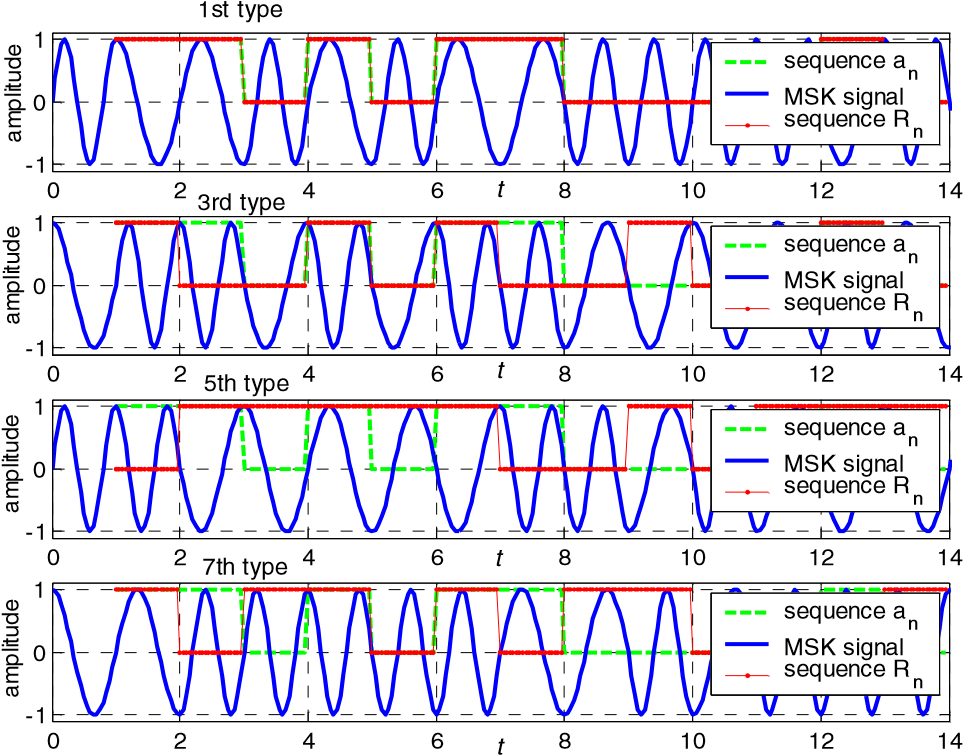Рисунок 2. Сигналы MSK, генерируемые с использованием различных методов генерации, и соответствующие сообщения, восстановленные с помощью базового демодулятора

С помощью программного обеспечения MATLAB сигнал MSK может быть сгенерирован в соответствии с методами, перечисленными в ТАБЛИЦЕ I. В order для легкого наблюдения мы позволяем T_b = 1, f_c = 1/T_b, затем f₁ = 1,25/T_b, f₂ = 0,75/T_b. 2, показано построение некоторых выходных сигналов, которые генерируются для одних и тех же входных сообщений {a_n} в соответствии с 4 нечетными типами метода генерации в ТАБЛИЦЕ I. Из этих графиков видно, что: 1) все выходные сигналы соответствуют характерным сигналам сигналаMSK, что означает, что все они являются сигналами MSK; 2) формы сигналов выходного сигнала, генерируемые с использованием различных методов, различны, хотя их входные сообщения одинаковы; 3) выходные сигналы, генерируемые с использованием различных методов, не могут бытьизменены во временной области. Замечено, что любой тип сигнала MSK может быть демодулирован с помощью другого типа демодулятора MSK, в то время как восстановленные сообщения неверны. Соответствующие сообщения, восстановленные с помощью базового демодулятора, также строятся как the последовательность R_n на рис. 2. Из этих графиков мы видим, что восстановленные сообщения отличаются, и только сообщения первого типа совпадают с входными сообщениями. Другими словами, сигнал MSK может быть правильно демодулирован только демодулятором с типом same в качестве модулятора. Если получатель не знает структуру модулятора, невозможно правильно восстановить реальные исходные сообщения. Поэтому, если структура модулятора передатчика изменяется непрерывно, приемник не может правильно восстановить реальные исходные сообщения, передаваемые без изменения правила структуры модулятора MSK. Это означает, что с учетом модулированной формы сигнала структура модулятора MSK имеет определенную функцию шифрования формы сигнала для входных сообщений. Более того, этот процесс шифрования может быть реализован полностью на физическом уровне, который не может быть легко обнаружен третьей стороной коммуникаций. Эта разновидность структуры модулятора MSK может открыть новый путь для применения MSK modulation для передачи информации безопасности.

См. A SECURITY TRANSMISSION SCHEME BASED ON THE VARIABLE MSK MODULATOR

Рассмотрим модель системы беспроводной передачи, изображенную на рисунке 3. Источник связывается с пунктом назначения, и один подслушивающийего слушатель подслушивает передачу. В источнике сообщения модулируются модулятором MSK, а затем передаются в пункт назначения. Ссылаясь на идею частотно-скачкообразной связи, структура модулятора MSK может быть изменена в соответствии с секундойt между источником и пунктом назначения, которая не известна подслушивающему устройству. Чтобы получить низкую вероятность перехвата на подслушивающем устройстве, секрет должен иметь псевдослучайный паттерн, такой как последовательность М. Для удобства предположим, что messages передаются каждым кадром, а структура модулятора MSK фиксируется над кадром и изменяется от кадра к кадру в соответствии с секретом.



Рисунок 3. Модель системы: источник связывается с пунктом назначения, один подслушивающий подслушивает передачу

Поскольку правило изменения структуры модулятора MSK в источнике известно месту назначения, принятый сигнал может быть правильно демодулирован в пункте назначения с помощью демодулятора с соответствующей структурой. Хотя подслушивающий может обнаруживать принятые сигналы как сигналы MSK и демодулировать их, он не может правильно восстановить переданные сообщения, поскольку он не знает изменяющегося правила. Таким образом, передаваемые сообщения могут быть защищены в безопасности.

Замечено, что схема передачи, предложенная в данной работе, изменяет структуру модулятора, относящуюся к идее частотно-скачкообразной связи, но она может получить большее преимущество, чем частотно-скачкообразная связь. Во-первых, изменение частоты в частотно-скачкообразной связи может быть легко обнаружено в частотной области, как одно заметное изменение; при этом изменение структуры модулятора в нашей схеме не имеет какой-либо отметки во временной и частотной областях, и не может быть обнаружено третьей стороной связи. Во-вторых, хотя тип структуры модулятора MSK, приведенный в ТАБЛИЦЕ I, конечен, изменение между этими структурами является случайным, и невозможно правильно восстановить передаваемые сообщения с помощью демодулятора, соответствующего модулятору в ТАБЛИЦЕ I один за другим последовательно или в paralle1 вслепую. Поскольку любой тип демодулятора может демодулировать принятый сигнал, атранс-сбрасываемые сообщения неизвестны получателю в коммуникациях, невозможно судить, какие восстановленные сообщения являются реально передаваемыми. С этой точки зрения наша схема безопасна. В-третьих, секретный ключ нужен для управления изменением модулятора наструктуру демодулятора, а его безопасность является основой информационной безопасности в нашей схеме, поэтому кажется, что он недостаточно безопасен, как традиционный секретный ключ шифрования. На самом деле, замечено, что секретный ключ в нашей схеме напрямую не применяетсяd к передаваемым сообщениям, даже если он получен, к сожалению, подслушивающим устройством, подслушивающий не может расшифровать демодулированные сообщения без каких-либо инструкций об этом, так как нет ничего примечательного об изменении модуляторной структуры в передаваемом сигнале MSK. Таким образом, можно видеть, что наша схема по-прежнему безопасна с учетом шифрования с секретным ключом.

В. SECURITY ANALYSIS И SIMULATION RESULTS

В [1] автор показал, что информационную безопасность можно оценить с точки зрения BER. Целью информационной безопасности является то, что пункт назначения может получать передаваемые сообщения максимально правильно, а подслушивающий может получать их правильно какможно чаще. Это означает, что BER → 0 в пункте назначения, а BER → 0,5 в подслушивающем устройстве. В этом разделе мы теоретически анализируем безопасность вышеуказанной схемы передачи по каналу AWGN (добавление белого гауссовского шума) в терминах BER at подслушивающего устройства, а затем моделируем ее с помощью программного обеспечения MATLAB.

А. Теоретический анализ

Рисунок 4. Базовый демодулятор MSK

Поскольку существует 8 типов сигналов MSK, например, мы демодулируем их с помощью базового демодулятора MSK, как показано на рисунке 4 соответственно. Другие типы демодуляторов MSK также могут использоваться аналогичным образом. Здесь мы предполагаем, что правило отображения sy mbol на модуляторе заключается в том, что если передается '0', _{a i} = +1, и если '1' передается, _{a i} = −1, то соответствующее правило принятия решения заключается в том, что если dX > 0, принимается решение, что '0' передается, и если dX < 0, принимается решение, что '1' передается для ветви I и Q ветвь, где dX обозначает статистику окончательного решения ветви I или Q.

1) Первый тип сигнала MSK, подлежащего демодуляции

Во-первых, мы предполагаем, что первый тип сигналов MSK в TABLE I демодулируется, а затем демодулятор имеет тот же тип, что и модулятор. Здесь принятый сигнал может быть выражен как y(t)=s_MSK(t)+n_c(t)+n_s(t) (3)

где n_c(t) и n_s(t) — внутрифазная и квадратурная составляющие канального шума n(t), соответственно. Шум n(t) рассматривается как белый гауссовский с двусторонней плотностью спектра мощности n₀/2.

Окончательная статистика решений dI для I отрасли может быть получена как

dI 2 b ⎡⎣ f t i A f t f t n t ⎤⎦dt

+ b (2i+2)Tb (4)

= A/4 a _i − πf t dt_d + n t_c ( )sin2πf t_d cos2πf tdt_c

iT b b

= 0,5а_{2 1i}+ AT_b +n_I

Шум n_I не зависит от одного образца к другому, с одинаковой дисперсией

n tc f td f t dtc n T0 b /4 (5) nI ⎢⎣ 2 b ⎥⎦

Таким образом, dI можно рассматривать как гауссовскую случайную величину со средним d = _2i+1AT_b/2 и дисперсией σ² = n₀T_b/4. Условный PDF (функция вероятности density) dI для '0' и '1' в качестве передаваемого сообщения может быть выражен как

f0( )x = 2πσ1 2 exp⎛⎜⎝−2σ12 (x − d )2⎞⎟⎠ (6)

f x1( ) = 21 2 exp⎛⎜− σ12 (x + d )2⎞⎟⎠ πσ ⎝ 2

Согласно правилу принятия решения, BER I филиала можно получить как

P_eI 0.5 f x dx( ) 0.5 f ( )x dx 0.5erfc( E_b / n₀ ) (7)

где E_b=A²T_b/2 — битовая энергия передаваемого сигнала MSK, а erfc(⋅) — функция комплементарной ошибки. Аналогичным образом, мы также можем получить BER ветви Q как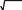

PeQ = 0,5erfc( Eb /n0 ) (8)

Как правило, сообщения для ветвей I и Q независимы. Тогда BER в точке B на рис.4 можно получить как

P_eB1 = 0,5P_eI + 0,5P_eQ = 0,5erfc( E_b / n₀ ) (9)

После дифференциального декодирования BER сигнала MSK по каналу AWGN может бытьлегко сохранен как

Pe1=2PeB1=erfc( E nb/ 0) (10)

2) Второй тип сигнала MSK, подлежащего демодуляции

Далее рассмотрим второй тип сигнала MSK в ТАБЛИЦЕ I демодуляцией. Поскольку сигнал для I ветви такой же, как и у первого типа, итоговая статистика решений dI и BER для I ветви может быть такой же, как (4) и (7).

Аналогичным образом, статистика final решений dQ для ветви Q может быть получена как

(2 3) i+ T_b

dQ =−A/4∫(2 1)i₊ Tb a_2i+2 (1+cos4πf t dt_d ) + = +n_Q d_Q n_Q (11)

Здесь d_Q равен отрицательному значению d_Q в предыдущем случае. И тогда dQ можно рассматривать как гауссовскую случайную величину со средним d = −a_2i+2AT_b/2 и дисперсией σ² = n₀T_b/4. В базовом демодуляторе правило принятия решения не может изменяться с изменением входного сигнала. И тогда, подобно предыдущему случаю, BER ветви Q можно получить как

PeQ = −1 0.5erfc( Eb /n0 ) , и тогда BER в точке B на рис.4 может быть обтained как

P_eB2 = 0,5P_eI + 0,5P_eQ = 0,5 (12)

Согласно приведенному выше анализу, мы можем обнаружить, что восстановленные сообщения в ветви I являются все ожидающими, а те, что в ветви Q, являются отрицательными от ожидающих, когда шум канала не учитывается. Тогда входные сообщения дифференциального декодера являются правильными и ложными в свою очередь, а после дифференциального декодирования BER сигнала MSK по каналу AWGN можно легко получить, как

P_e2=2P_eB2=1 (13)

3) Третий тип сигнала MSK, подлежащего демодуляции

Далее рассмотрим третий тип сигнала MSK в ТАБЛИЦЕ I для демодуляции. Как и в предыдущем случае, окончательное решение статистики dI равно dI = A ⎡a2i ∫2(2 1)iTib+ Tb sin4πf tdtd + a2 2i+ ∫(2 1) ii++ TTbb π f tdtd ⎤⎦⎥+ = +nI dI nI (14) 4 ⎢⎣

Когда sign(a_2i) = sign(a_2i+2), где sign(⋅) — функция signum,

dI = 0,25Aa i sin4 f tdtd = 0 (15)

2 _б

dI — это просто шум n_I. И когда знак (_2i) ≠ знак (знак_{2i + 2}),

d Aa T_I = _{2i b} ^/π=−Aa T_{2 2i}+ _b ^/π (16)

dI становится сигналом принятия решения для передаваемых_2i или _2i+2, в то время как он должен быть сигналом решения для _2i+1, передаваемых фактически. В общем, передаваемые сообщения случайны и независимы в коммуникациях, поэтому вероятность того, что _2i+1 совпадает с_2i или _2i+2 равна 1/2. Тогда BER I ветви составляет около 1/2. Аналогично приведенному выше анализу для ветви I, BER ветви Q также получается как около 0,5. Тогда BER в точке B на фиг.4 и после дифференциального декодирования могут быть получены как

P_e3 = P_eB3 = 0,5P_eI + 0,5P_eQ = 0,5 (17)

так как все битовые ошибки ветвей I и Q случайны с вероятностью 0,5.

Как и в вышеуказанных случаях, BER для других типов сигналов MSK, подлежащих демодуляции, может быть получен, как показано в ТАБЛИЦЕ II. Подробностине представлены в настоящем документе с учетом ограничений по страницам.

ТАБЛИЦА II. БЕР Т ХЭ 4-Й 8-Й ТЯП МСК СИГНАЛЬ БУДЕТ ЭМОДУЛИРОВАН

Тип	4-й тип	5-й тип	6-й тип	7-й тип	8-й тип
БЕР I филиала	PeI = 0,5	PeI = 0,5	PeI = 0,5	PeI = 0,5	PeI = 0,5
BER филиала Q	PeQ = 0,5	PeQ = 0,5	PeQ = 0,5	PeQ = 0,5	PeQ = 0,5
BER в точке B	PeB4 = 0,5	PeB5 = 0,5	PeB6 = 0,5	PeB7 = 0,5	PeB8 = 0,5
БЕР	е4= 0,5	е5= 0,5	е6= 0,5	е7= 0,5	е8= 0,5

Теперь мы предполагаем, что изменение структуры модулятора MSK полностью случайно, а затем вероятность того, что любой тип сигнала MSK передается, равна, и все равно 1/8,

так как существует 8 типов передаваемых сигналов MSK. Так, средний BER новой схемы по каналу AWGN можно получить как

8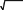

P_e = 0,125∑P_ei = +0,5 0,125erfc( E_b / n₀ ) ≈ 0,5 (18)

i=1

B. Результаты моделирования

В этом разделе BERсхемы n EW моделируется с помощью программного обеспечения MATLAB. Здесь мы предполагаем, что в качестве секретного ключа используется M-последовательность длиной 16. Последовательность М и две ее сдвинутые последовательности используются в качестве управляющих сигналов для весовой функции, модулированной несущей и комбайнаторноймодулятора для изменения структуры модулятора среди 8 типов, перечисленных в ТАБЛИЦЕ I соответственно. Пусть подслушивающий может обнаружить передаваемый сигнал MSK и демодулировать принятый сигнал с помощью базового демодулятора, потому что ничего не имеет о сигналеэкрета s. Фактически, последовательность M может быть легко сгенерирована, и модификация каждого модуля может быть легко реализована переключателем, управляемым назначенным управляющим сигналом. С этой точки зрения новая схема не может принести большой сложности увеличения по сравнению с традиционной системой передачи модуляции MSK.

0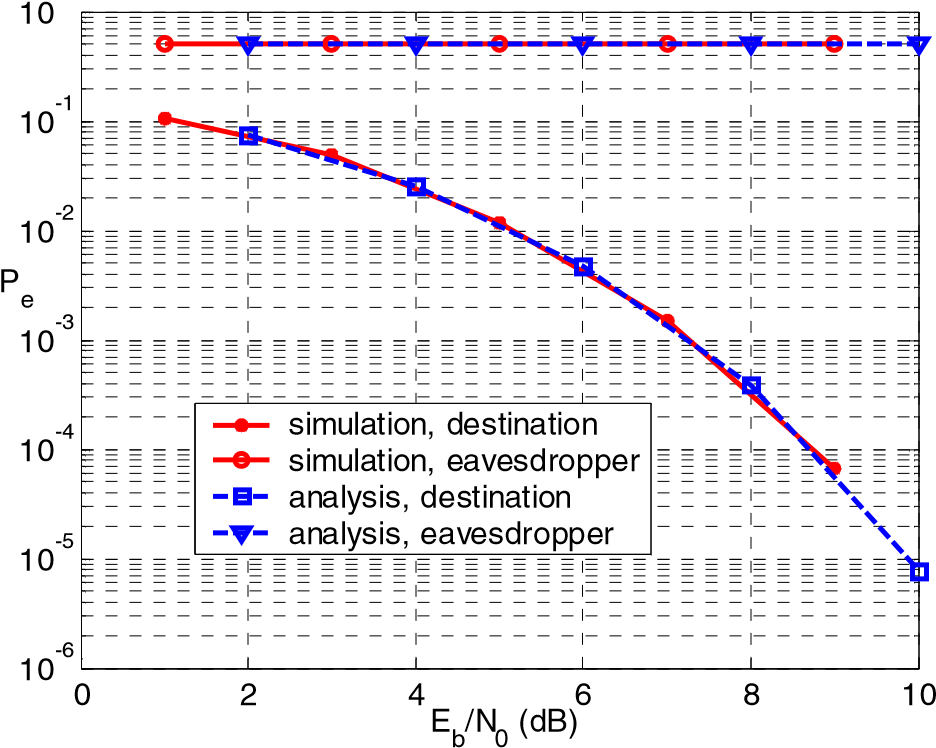

Рисунок 5. BERs в пункте назначения и подслушивающий

BERs в пункте назначения и подслушивающий устройство изображены на рисунке 5, соответственно. Здесь кривые анализа на фиг.5 получены согласно (10) и (18). Из этих кривых видно, что в новой схеме BER на подслушивающем устройстве достигает примерно 50% во время измерений для различных значений SNR, что почти эквивалентно случайному угадыванию передаваемых сообщений, тем самым обеспечивая связь между источником и пунктом назначения.

V. CОНКЛЮЗИЯ

В статье исследуются модифицированные методы генерации сигнала MSK и представлены 8 типов структур модуляторов MSK. Результаты показывают, что структура модулятора MSK имеет определенную функцию шифрования формы сигнала для входных сообщений. Исходя из этого вывода, в данной работе предложена одна новая схема защищенной передачи с модуляцией MSK, где структура модулятора MSK может быть изменена в соответствии с секретом между источником и пунктом назначения. BER этой схемы анализируется теоретически и моделируетсяс помощью программного обеспечения MATLAB. Результаты показывают, что предложенная схема может обеспечить высокую безопасность передачи с точки зрения BER и низкую сложность увеличения. Фактически, наша идея может быть применена к системе с другими форматами модуляции, такими как MPSK или MQAM.

REFEРЕНСЕС

1. 
   А.Д. Уайнер, «Канал проводного подключения», Bell Syst. Tech. J., vol. 54, no. 8, pp. 1355-1387, 1975.
   
2. 
   Y.S. Shiu, S.Y. Chang, H.C. Wu, S.C.H. Huang and H.H. Chen, "Physical layer security in wireless networks: a tutorial," IEEE wireless Communications, vol.18, no.2, pp. 66-74, 2011.
   
3. 
   Л. Чен, «Безопасность физического уровня для совместного ретрансляции в вещательных сетях», Конференция по военной связи 2011 года, стр. 91-96, 2011 год.
   
4. 
   L. Dong, Z. Han, A.P. Petropulu and H.V. Poor, "Improving wireless physical layer security through cooperating relays," IEEE Transactions on Signal Processing, vol. 58, no. 3, pp. 1875-1888, 2010.
   
5. 
   B. Raef, E. Ersen, H. Xiang, T. Ender and X. Jian, "Cooperative security at the physical layer: a summary of recent advances," IEEE Signal Processing Magazine, pp. 16-28, 2013.
   
6. 
   X. Li, Z.Z. Gao, G.M. Lv and S.H. Zhu, "Generalized antieavesdropping space-time network coding for cooperative communications," 2013 IEEE Wireless Communications and Networking Conference, pp. 4163-4168, 2013.
   
7. 
   Y. Liu, L. Li and M. Pesavento, "Повышение безопасности физического уровня в ненадежных ретрансляционных сетях с искусственным шумом: подход, основанный на частоте ошибок символов", 2014 IEEE^8-й sensor Array and Multichannel Signal Processing workshop (SAM), стр. 261-264, 2014.
   
8. 
   M.I. Husain, S. Mahant and R. Sridhar, "CD-PHY: безопасность физического уровня в беспроводных сетях через разнообразие созвездий", 2012 MilCom, стр. 1-9, 2012.
   
9. 
   H. Zhang, B.N. Zhang, D.X. Guo, X.G. Wang and J. Chen, "Digital communications technology," Posts & Telecom Press, 2008.
   
10. 
    C.X. Fan, L.N. Cao, "Principles of communications", 6th edition, National Defense Industry Press, 2010.
    
11. 
    J.G. Proakis, "Digital communications", 4th edition, McGraw Hill Education Companies, 2001.