Коллоидная химия. Коллоидная химия Коллоидная химия наука о поверхностных явлениях и дисперсных системах. Поверхностное явление
 Скачать 1.77 Mb. Скачать 1.77 Mb.
|
|
Мономолекулрная адсорбция. Изотерма Лангмюра. Простейшие закономерности были получены в теории генри. Ленгмюр предложил теорию, согласно которой, адсорбция рассматривается как квазихимическая реакция. При этом:
Зависимость адсорбции от концентрации 1 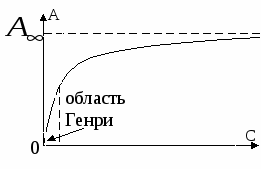 ) ) 2) область высоких концентраций Для энергии Гиббса: g – энтропийный множитель. В случае изотермы Генри энергия Гиббса характеризует переход адсорбата из стандартного состояния в объёме в стандартное состояние на поверхности. В случае изотермы Ленгмюра 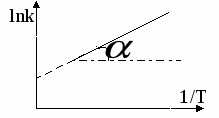 , тогда , тогда 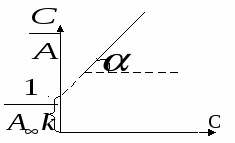 Т.е. в области высоких концентраций число свободных мест обратно пропорционально количеству адсорбата. Адсорбция смеси газов на однородной поверхности. В этом случае процесс адсорбции рассматривают как две параллельно протекающие реакции. 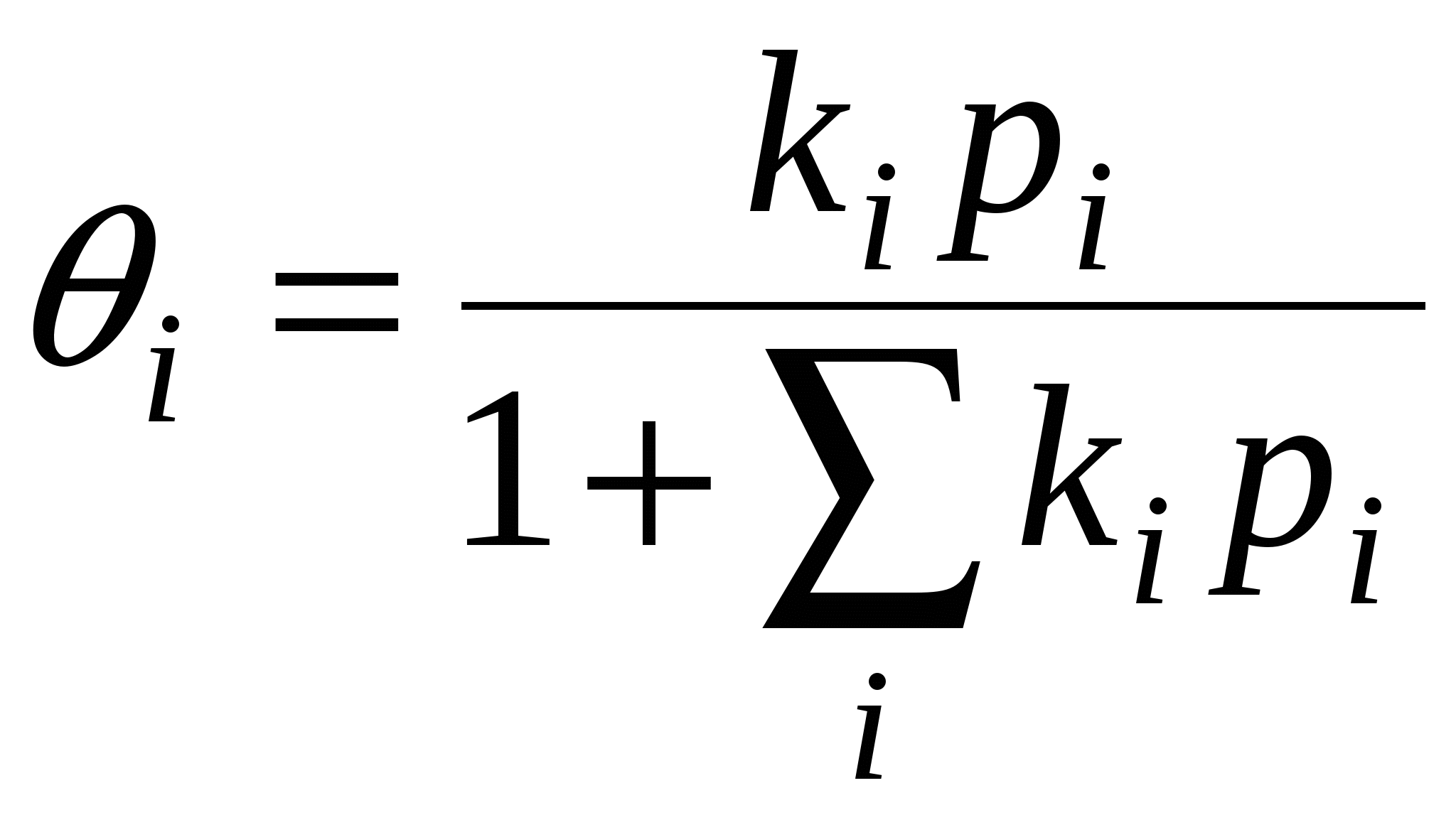 Адсорбция смеси газов на неоднородной поверхности.
В этом случае отношение
«+» - симбатная зависимость, «-» - антибатная зависимость, «Н» - корреляции нет. «+» - адсорбция протекает по одинаковому механизму. На наиболее энергетически выгодных участках преимущественно адсорбируется газ, обладающий большим сродством к поверхности. «-» - адсорбция протекает по различным механизмам и до определенного момента времени конкурентной борьбы за поверхность нет. Мономолекулярная адсорбция преимущественно реализуется при физической адсорбции газов при малых значениях p, а также на границе раздела жидкость/газ. Полимолекулярная адсорбция. Теория БЭТ (Брунауэр, Эммет, Теллер). В случае, когда образование монослоя недостаточно для компенсации поверхностной энергии, адсорбция полимолекулярна и её можно рассматривать как результат вынужденной конденсации под действием поверхностных сил. Основные положения:
П  оверхность рассматривается как совокупность адсорбционных мест. Справедливо условие динамического равновесия: скорость конденсации на свободных местах равна скорости испарения с занятых. оверхность рассматривается как совокупность адсорбционных мест. Справедливо условие динамического равновесия: скорость конденсации на свободных местах равна скорости испарения с занятых. a – коэффициент конденсации (доля молекул, сконденсировавшихся на поверхности); Zm – максимальное число свободных мест. Для первого слоя условия динамического равновесия: 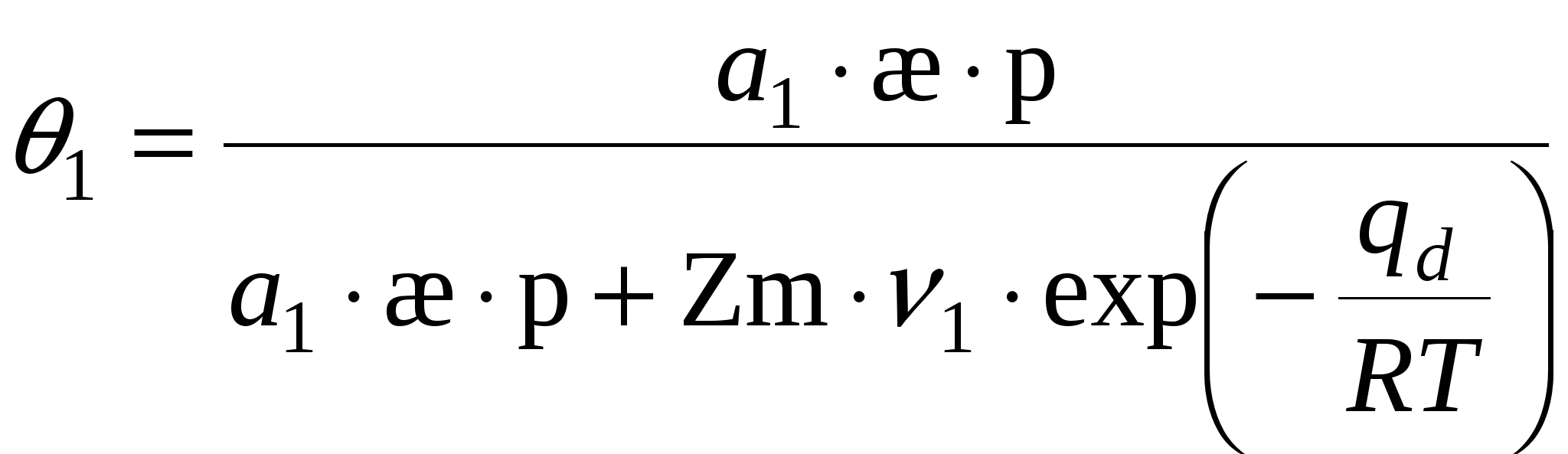 Для второго слоя будет справедливо: Для i-го слоя: Для упрощения принимают, что а и ν одинаковы для всех слоев, кроме первого. Для всех слоев кроме первого теплота адсорбции постоянна. Для последнего слоя теплота адсорбции равна теплоте конденсации. В результате было получено уравнении 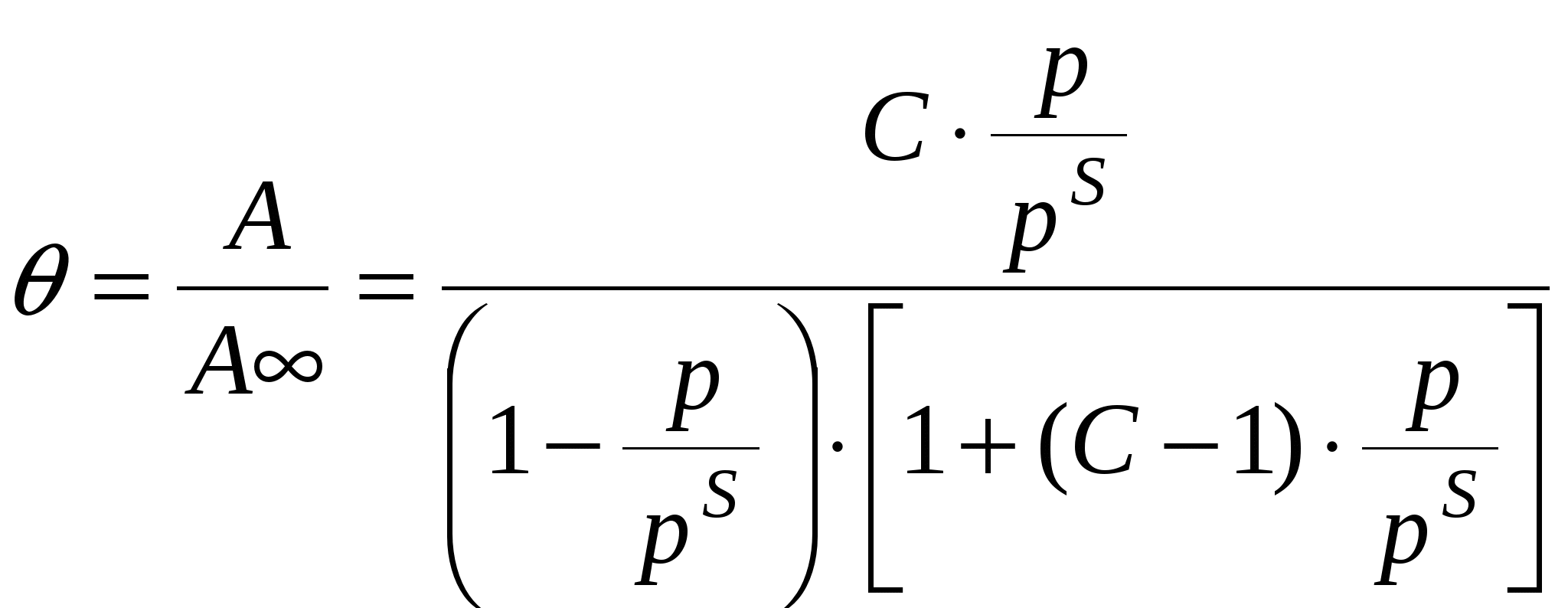 (*) (*)C – константа, В случае теории БЭТ, константа С характеризует энергию Гиббса чистой адсорбции. Уравнение содержит только одну константу, а также это уравнение очень важно для определения удельной поверхности адсорбента. Поскольку в результате адсорбции теплота выделяется, определение удельных поверхностей ведут при низких температурах. 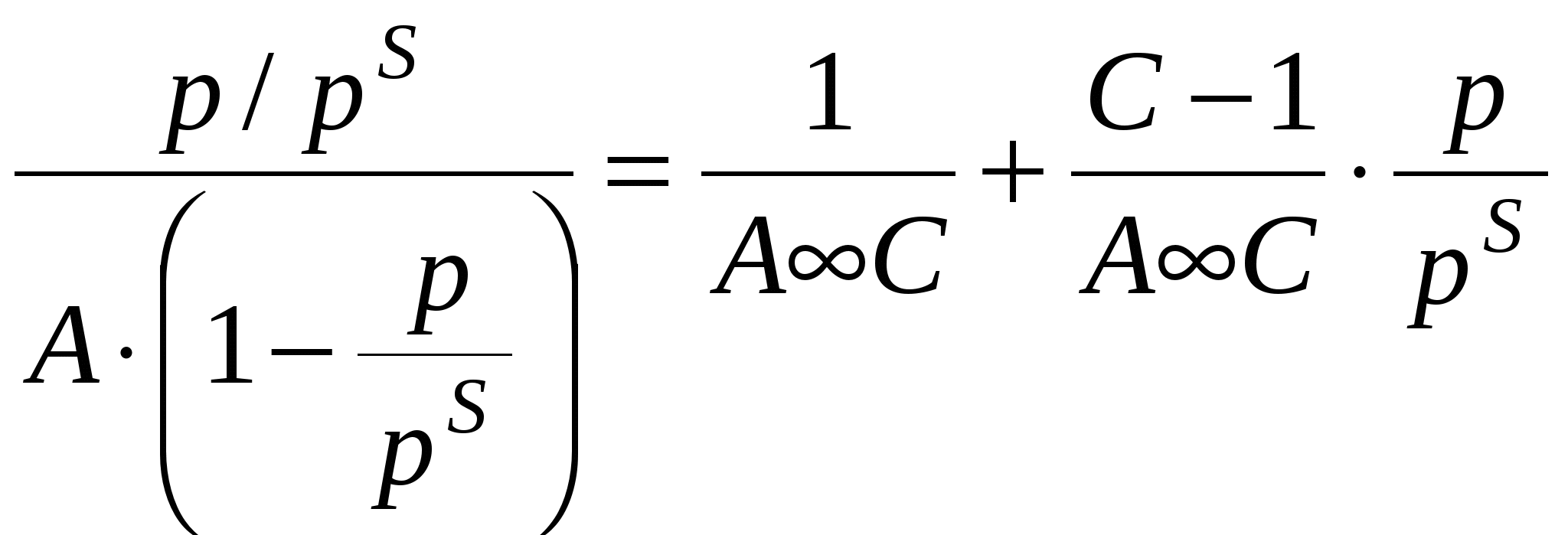 ???????????? ????????????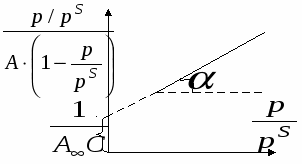 Основной недостаток теории – пренебрежение горизонтальными взаимодействиями в пользу вертикальных. Уравнение выполняется в области значений Там, где Учет взаимодействий адсорбат-адсорбат. Взаимодействия проявляются при адсорбции на неполярной поверхности разветвленных молекул или молекул. Способных образовывать ассоциаты. В этом случае изменяется форма изотерм адсорбции. А 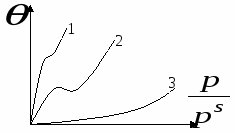 дсорбент не полярен. дсорбент не полярен. Графику 1 соответствуют слабые взаимодействия адсорбат-адсорбат, сильное адсорбат-адсорбент. Графику 2 соответствуют сильное взаимодействие адсорбат-адсорбат, сильное адсорбат-адсорбент. Графику 3 соответствуют сильное взаимодействие адсорбат-адсорбат, слабое адсорбат-адсорбент. В случае взаимодействия между молекулами адсорбата необходим учет изменения коэффициентов активности. И это уравнение записывают в виде: k – аттракционная постоянная. Потенциальная теория Поляни. Данная теория не выводит какого-либо типа изотермы адсорбции, а дает возможность расчета изотерм при другой температуре. Адсорбция – это результат притяжения адсорбата к поверхности адсорбента за счет действия адсорбционного потенциала, который не зависит от присутствия других молекул и зависит от расстояния между поверхностью и молекулой адсорбата. Поскольку поверхность неоднородная, расстояние заменяют на адсорбционный объём Адсорбционный потенциал – это работа перенесения 1 моль адсорбата вне данного адсорбционного объёма в данную точку адсорбционного объёма (или работа переноса 1 моль насыщенного пара адсорбата, находящегося в равновесии с жидким адсорбатом в отсутствии адсорбента в равновесную с адсорбентом паровую фазу). Х 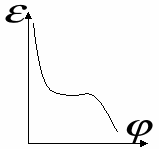 арактеристическая кривая арактеристическая криваяДля данного адсорбента и различных адсорбатов справедливо: Для разных типов адсорбатов 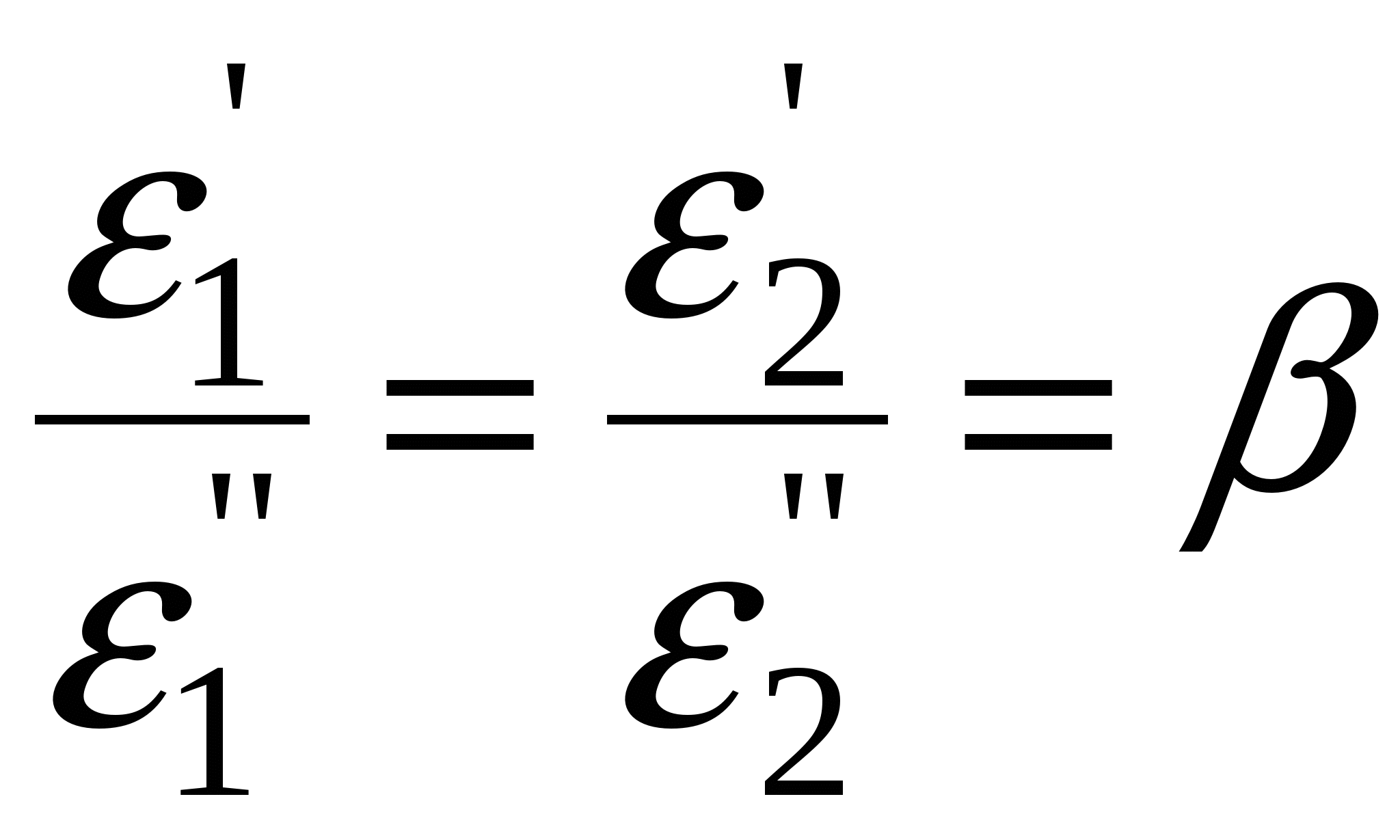 , ,где Теория капиллярной конденсации. Протекание процесса адсорбции во многом зависит от структуры пористого тела.
В случае микропористых сорбентов, поля адсорбционных сил перекрываются. В случае макропористых сорбентов, поры выполняют роль транспортных каналов. Процессы коденсации наиболее значимы в переходнопористых телах. Капиллярная конденсация начинается при определенных значениях p и 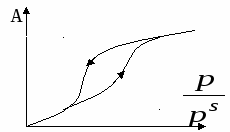 - для случая смачивания, центр кривизны находится в газовой фазе. - для случая смачивания, центр кривизны находится в газовой фазе.В случае капиллярной конденсации изотерма адсорбции имеет гистерезисный вид. Процессу адсорбции соответствует нижняя ветвь, процессу десорбции – верхняя. Все виды пор можно свести к трем видам:
В 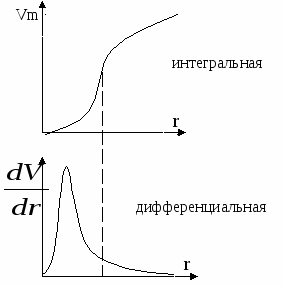 условиях смачивания конденсация осуществляется при более низких давлениях, что энергетически выгодно. По десорбционной ветви получают кривые распределения пор по размерам. условиях смачивания конденсация осуществляется при более низких давлениях, что энергетически выгодно. По десорбционной ветви получают кривые распределения пор по размерам. Максимум дифференциальной кривой смещен влево относительно точки перегиба интегральной. Общий объём малых пор невелик, однако имеет большие значения площади поверхности. С увеличением размера пор, их объём возрастает как | ||||||||||||||||||||||||||||||||||||||||||

 роцессное заполнение осуществляется со дна поры.
роцессное заполнение осуществляется со дна поры. 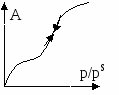
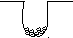
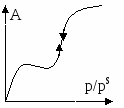 истерезиса нет. Прямой и обратный ход описываются уравнением:
истерезиса нет. Прямой и обратный ход описываются уравнением: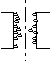 на нигде нет, заполнение поры пойдет по стенкам цилиндра.
на нигде нет, заполнение поры пойдет по стенкам цилиндра. 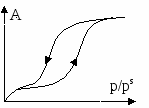 Изотерма и будет иметь гистерезисный вид.
Изотерма и будет иметь гистерезисный вид.