Коллоидная химия. Коллоидная химия Коллоидная химия наука о поверхностных явлениях и дисперсных системах. Поверхностное явление

• Название: Коллоидная химия Коллоидная химия наука о поверхностных явлениях и дисперсных системах. Поверхностное явление
• Дата: 23.01.2018
• Размер: 1.77 Mb.
• Имя файла: Коллоидная химия.doc
• Тип: Документы; #35001
• страница: 1 из 6

Коллоидная химия

Коллоидная химия – наука о поверхностных явлениях и дисперсных системах. Поверхностное явление – явление на границе раздела фаз.

Дисперсные системы – это многофазные системы, состоящие как минимум из двух фаз, одна из которых находится в мелкораздробленном состоянии.

Дисперсионная фаза (ДФ) – мелкораздробленная фаза, а дисперсионная среда (ДС)– это сплошная часть дисперсионной системы. Т. о., у дисперсных систем два признака: гетерогенность (качественный признак) и дисперсионность (количественный).

Дисперсность – величина, обратная линейному размеру частицы (м^-1): , где а – размер частицы.

Классификация:

1. 
   по степени дисперсности:
   
   • 
     высокодисперсные (10^-7- 10^-9 м ) – космическая пыль;
     
   • 
     среднедисперсные (10^-7 – 10^-5м) – чай, кофе;
     
   • 
     грубодисперсные (10^-5 – 10^-3м).
     
2. 
   по геометрическому признаку:
   

Система	Признак	Тип
Трехмерные	3	Объемные
Двумерные	2	Тонкие пленки
Одномерные	1	Капилляры

3. 
   по кинетическому состоянию ДФ
   

кинетическое состояние ДФ



свободнодисперсные связнодисперсные

(капиллярные тела)



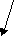Золи суспензии макропористые

микропористые (>200 нм)

(<2 нм) переходнопористые

Гели пасты (2 – 200 нм)

ДФ	ДС	Тип
Тв	Тв	Минералы
Тв	Ж	Коллоидные растворы
Тв	Г	Дым
Ж	Тв	Сок растений, почва
Ж	Ж	Эмульсии (молоко)
Ж	Г	Туман
Г	Тв	Твердые пены (капиллярно – пористые тела)
Г	Ж	Пены (мыльная)
Г	Г	Для коллоидной химии нет

4. 
   по энергии взаимодействия ДС и ДФ:
   

• 
  Лиофильные (сильное взаимодействие).
  
• 
  Лиофрбные (слабое взаимодействие).
  

5. 
   по величинам удельной поверхности:
   

- межфазовая поверхность

- для частиц сферической формы (м^-1)

S_уд всегда очень большая величина.
Поверхностная энергия G_S:

– полная поверхностная энергия системы.



Поверхностная энергия может преобразовываться в энергию Гиббса, тепловую работу, механическую работу, в работу химическую, в электрическую энергию.
Свойства дисперсных систем:

1. 
   Молекулярно – кинетические (диффузия, осмос, седиментация).
   
2. 
   Оптические (светопоглощение и светорассеяние).
   
3. 
   Электро-кинетические (электрофорес, электроосмос, потенциал седиментации, потенциал течения).
   

Молекулярно – кинетические свойства

МКТ рассматривает дисперсные системы с позиции истинных растворов, т. е. ДС – это растворитель, а ДФ – растворенное вещество. Выделяют следующие свойства: броуновское движение, осмос, седиментация. Для дисперсионных систем характерны два вида устойчивости:

• 
  Агрегативное – устойчивость по отношению к слипанию.
  
• 
  Седиментационная – по отношению к силе тяжести.
  

Седиментация.

Седиментация – это движение частиц под действием силы тяжести. Потеря седиментационной устойчивости ведет к расслаиванию системы.

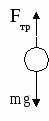В начальный момент времени mg>F_тр (равноускоренное движение).

В момент времени t, который соответствует установлению равновесие: .

Закон Стокса: 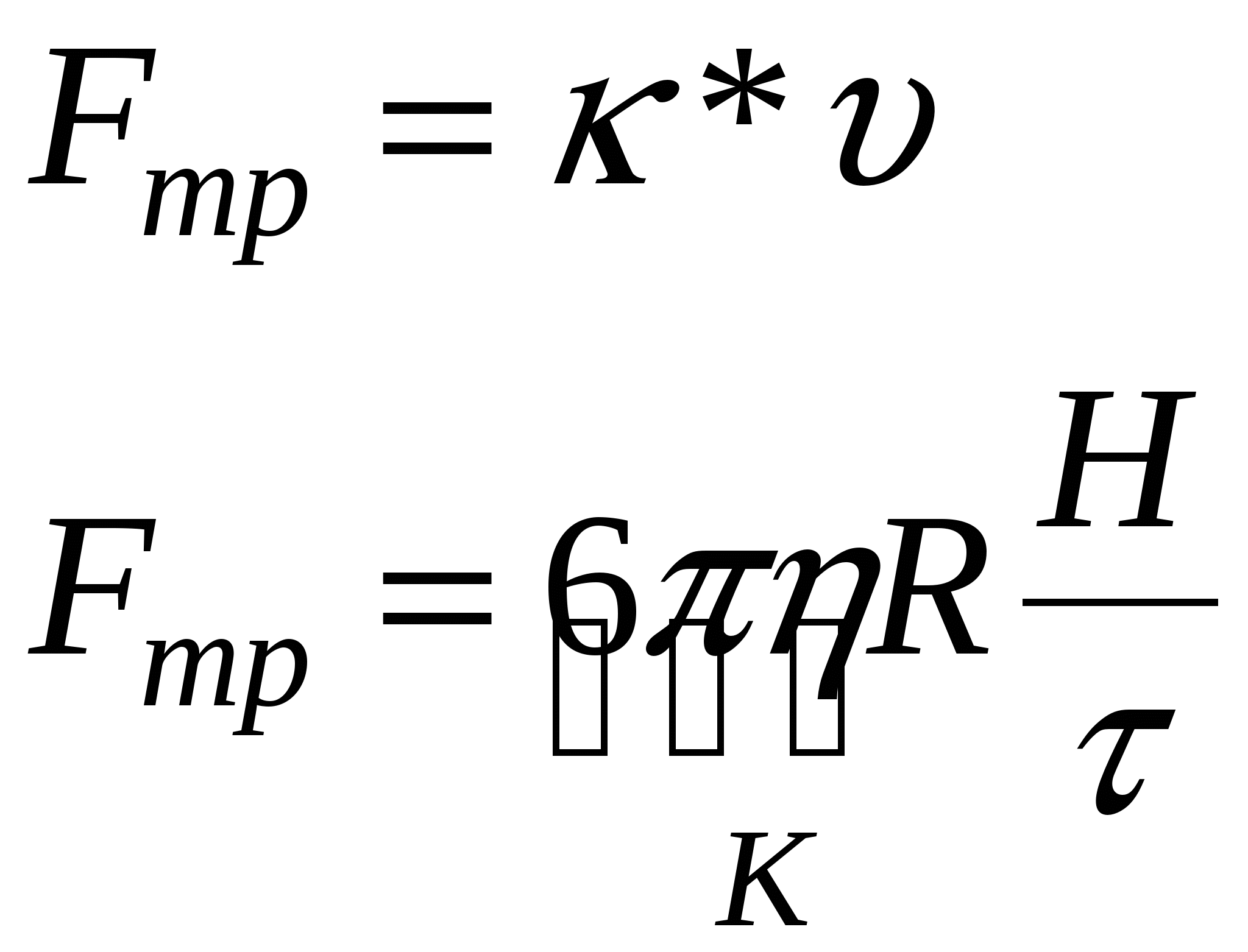, где

- коэффициент трения, R – радиус частицы, Н – высота, τ – время.



- плотность дисперсной фазы, - плотность дисперсионной среды

- основная формула седиментационого анализа: измеряя массы веществ, осевших в какой – либо момент времени, можно узнать размер этих частиц.



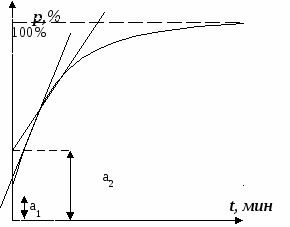
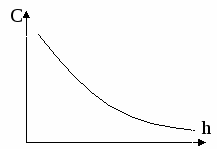
Кривая накопления (относительно изменения массы)- по ней находят кумулятивную фракцию - это доля частиц, осевших к данному моменту времени: .

Это отрезок, который отсекает на оси ординат касательная, проведенная к данной точке кривой накопления.

После диффиренцирования:
Максимум и точка перегиба совпадают:


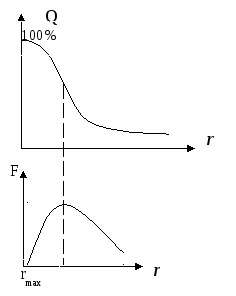
Система называется монодисперсной, если в ней преобладают частицы одного размера; если двух размеров – бидисперсная:

П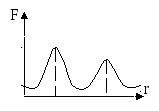оли дисперсная: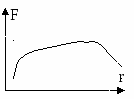



Диффузия.

Диффузия – это процесс, направленный на выравнивание концентраций в первоначально неоднородной среде. По своей сути противоположен седиментации.

S 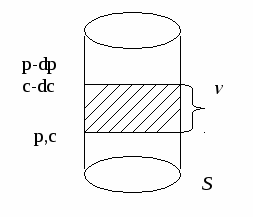– площадь поперечного сечения, p-dp, c-dc.Давление и концентрация меньше, ν - расстояние

Два уровня. Движущей силой процесса диффузии выступает градиент осмотического давления:

. В состоянии равновесия и для первой частицы справедливо: , – из закона Стокса.

N – число частиц (Na), С – концентрация, ν – высота

. - число частиц в объеме, диф. поток в единице времени, ν – линейная скорость движения, высота к единице поверхности.



Получаем диффузионный поток: , т. к. .

- 1-й закон Фика;


- уравнение Эйнштейна (коэффициент диффузии).
Поскольку все направления движения равновероятны, была предложена проекция среднеквадратичного сдвига:

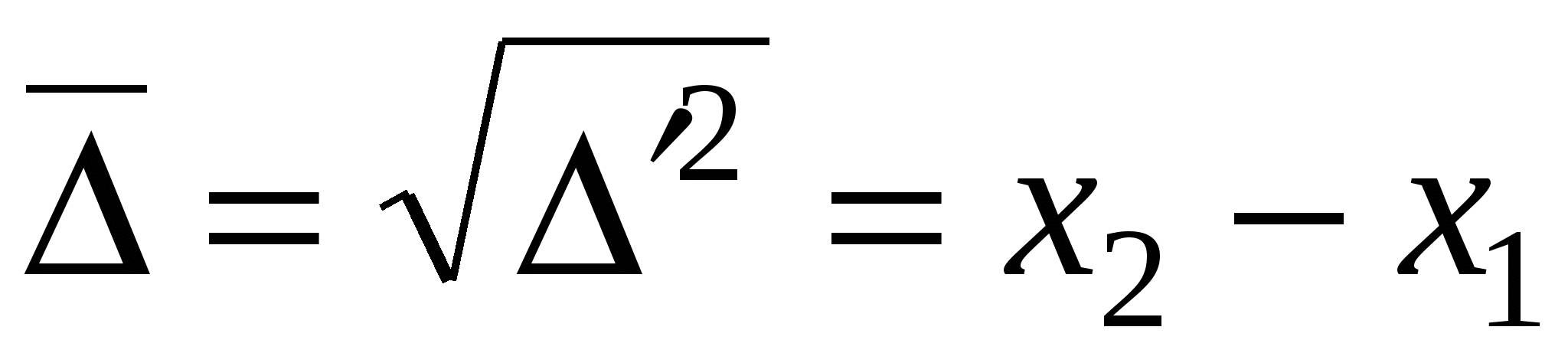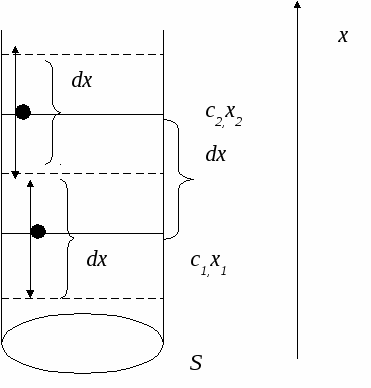, Идут вверх: ; идут вниз: .

Переносимая масса:

диффузионный поток в единицу времени через единицу поперечного сечения.

- по 1 – му закону Фика.

,




- уравнение для среднеквадратичного сдвига

D 10^-11 – 10^-14 м²/с, [D]=[м²/с]

Коэффициент диффузии – это поток вещества, переносимый через цилиндр с единичной площадью поперечного сечения в единицу времени.
Седиментационное диффузионное равновесие.

При условии постоянства Р и Т, т.е. при P=const, T=const.

Для системы, находящейся в состоянии равновесия справедливо: .

Если система находится в поле действия постоянной силы, то , где Е – поле силы тяжести.

- поле потенциальной силы.

Согласно уравнению Гиббса-Дюгема



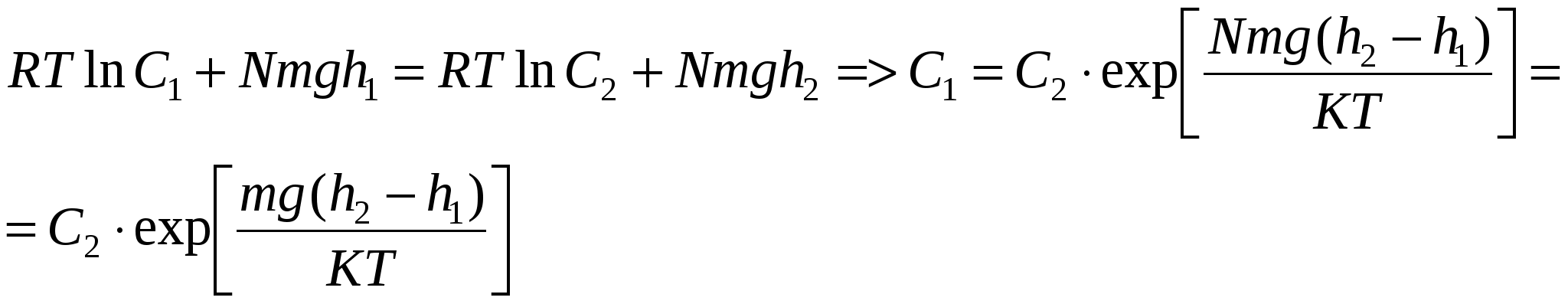
Пусть существует какой-то нулевой уровень, когда h₂=0, h₁=h.

С₁С, С₂=С₀

- гипсометрический закон, барометрическая формула.






Осмос.




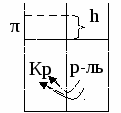
Осмосом называется движение растворителя (дисперсионной среды) к коллоидному раствору через полупроницаемую мембрану. Движущей силой осмотического процесса является неравенство химического потенциала по обе стороны от перегородки.
Кр = р-ль + ДФ, т.к. V₁ = V₂ = >



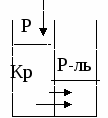
Чистка воды обратным осмосом:
Осмотическое давление рассчитывается по уравнению Вант-Гоффа: , С – концентрация, здесь [C] = [моль/м³].

, n – частичная концентрация

, Сm – массовая концентрация, m₀ – масса одной частицы, [n] = [м^-3].

Консервирс:

60 г/моль

30 г/моль 0,5 моль/л

,

Вирус: , толщина 10 мкм.

1. 
   Сm₁≠Cm₂, r₁ = r₂. Если растворы разной концентрации.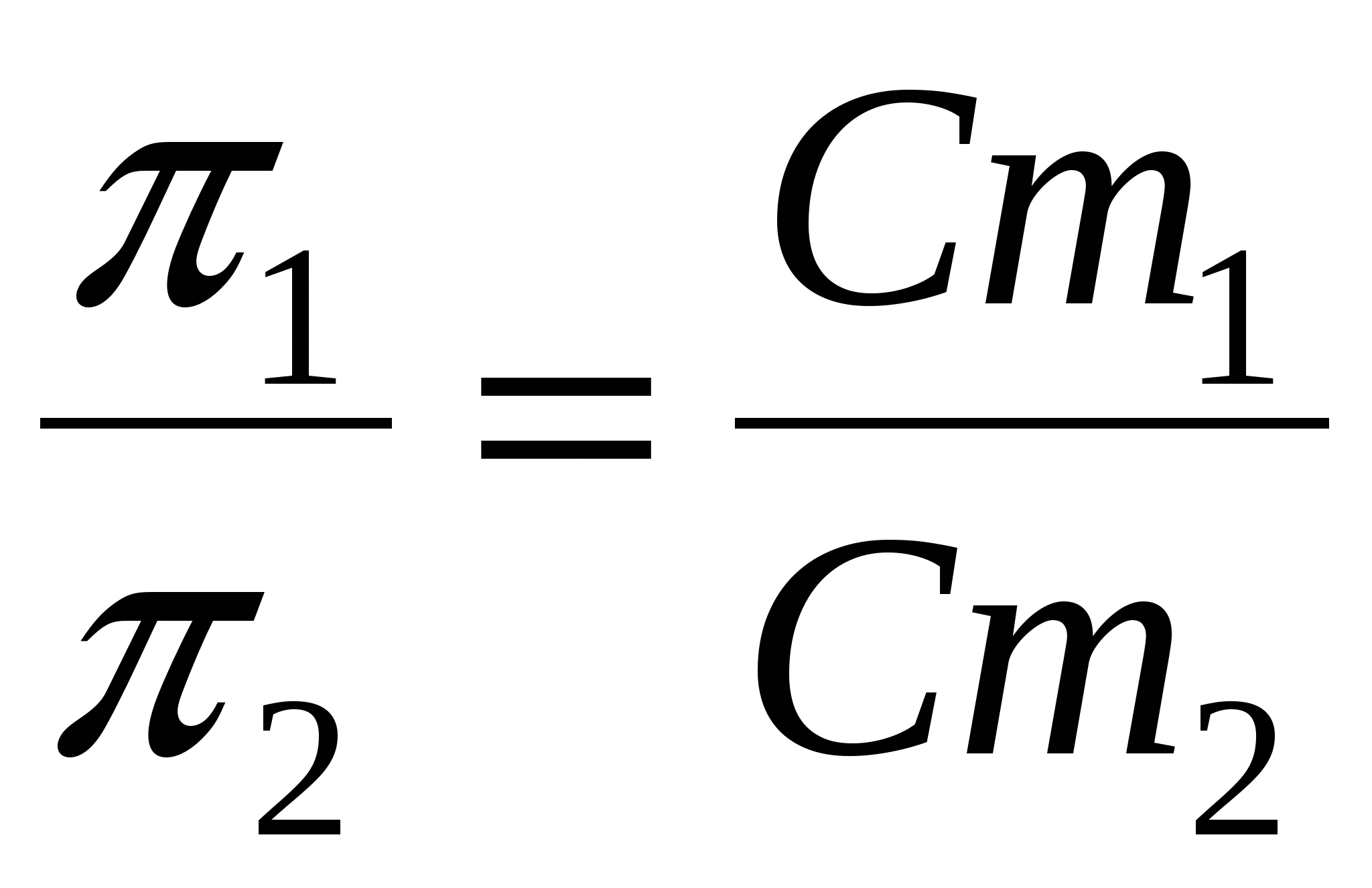
   
2. 
   Cm₁ = Cm₂, но r₁≠r₂. =>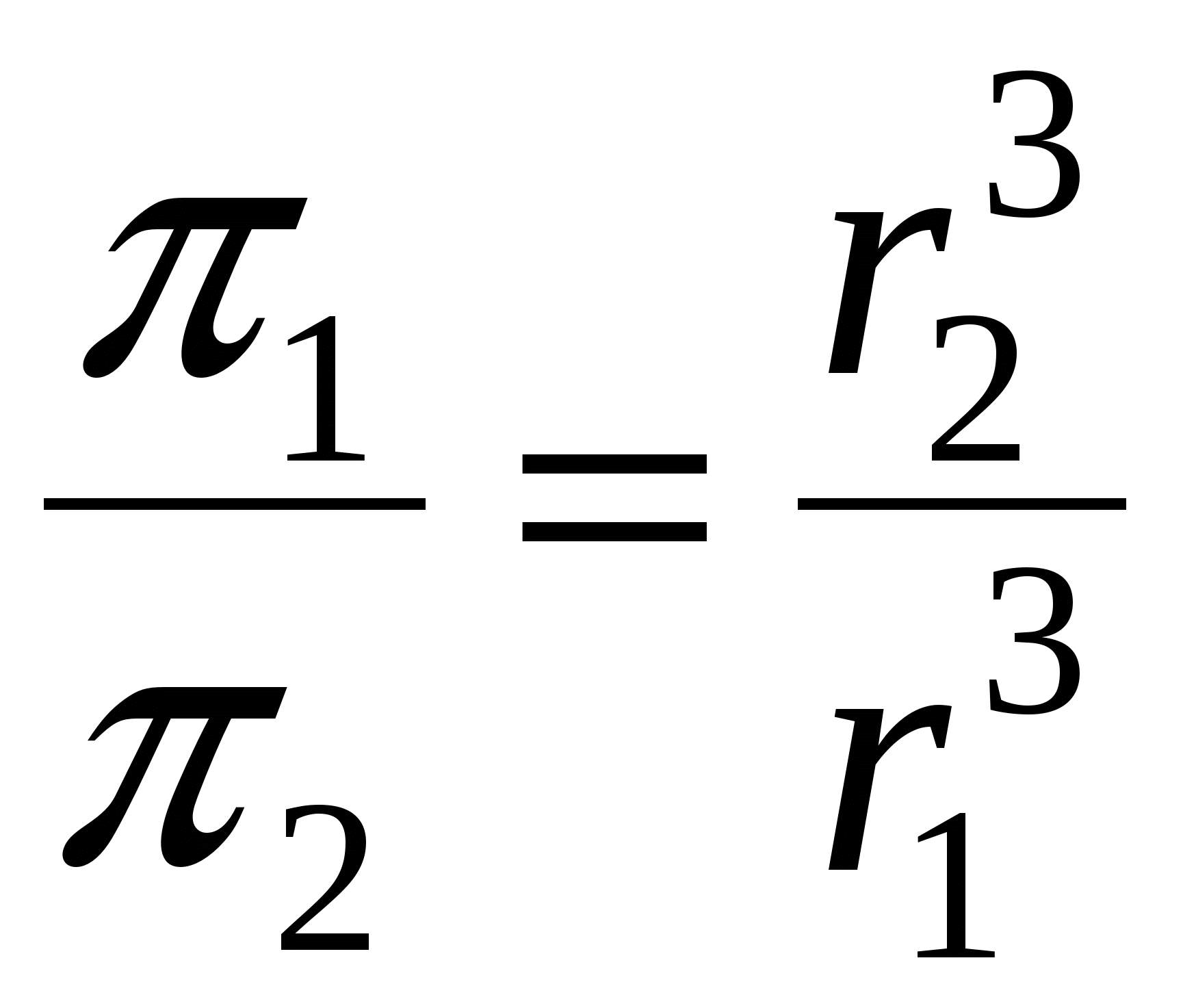 , т.к. 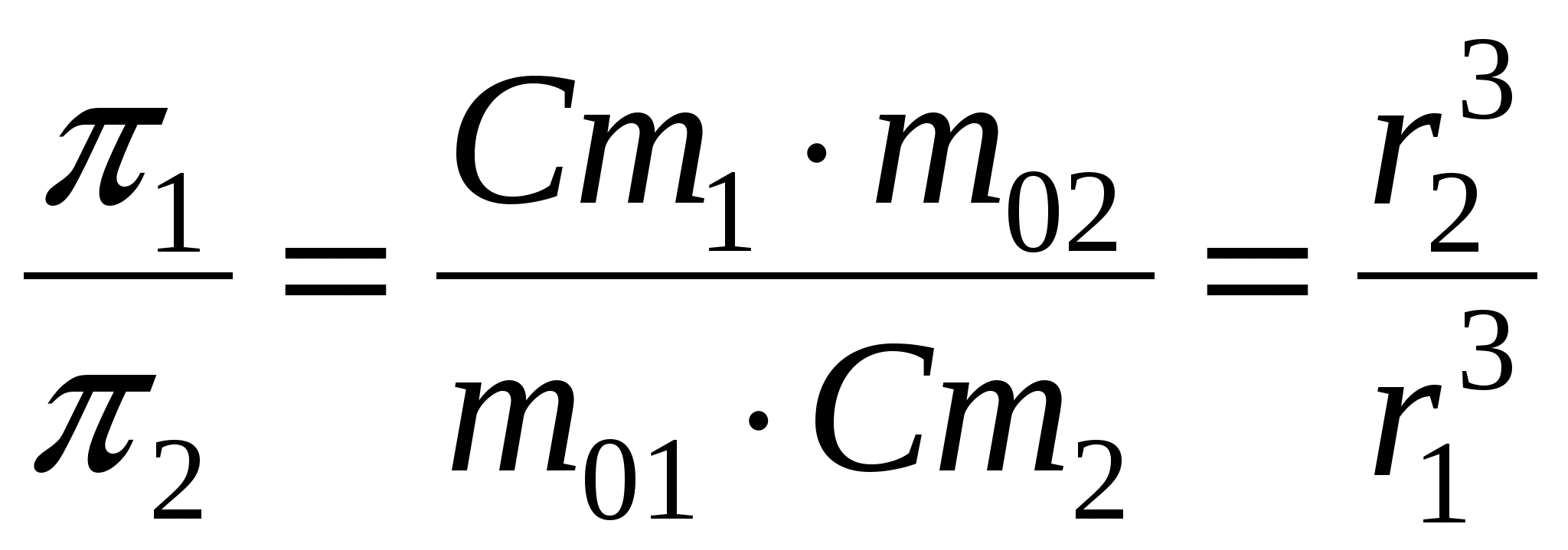; 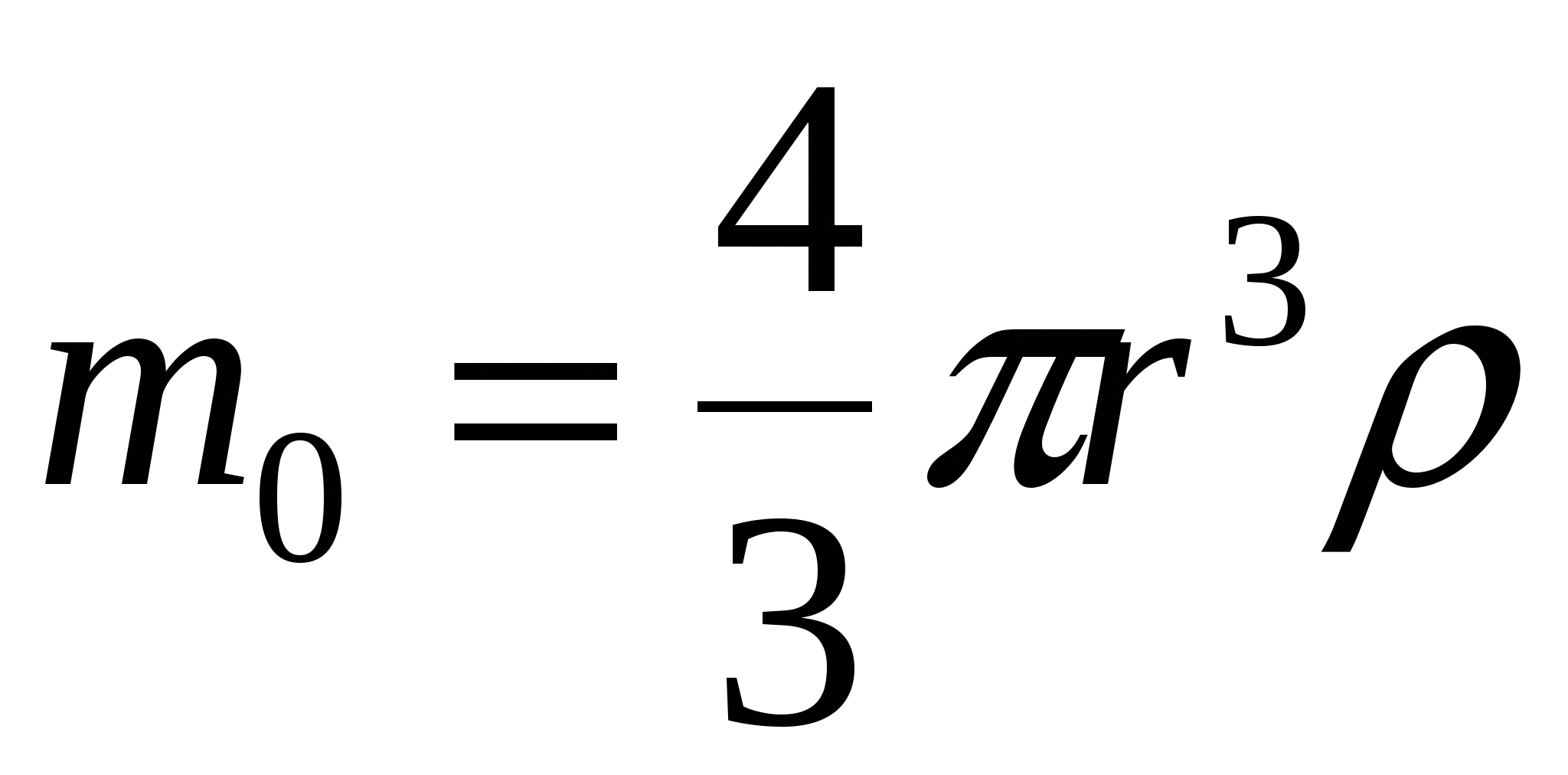, т.е. где r₁(ДФ) = 10^-7н и r₂(р-ль) = 10^-3 = >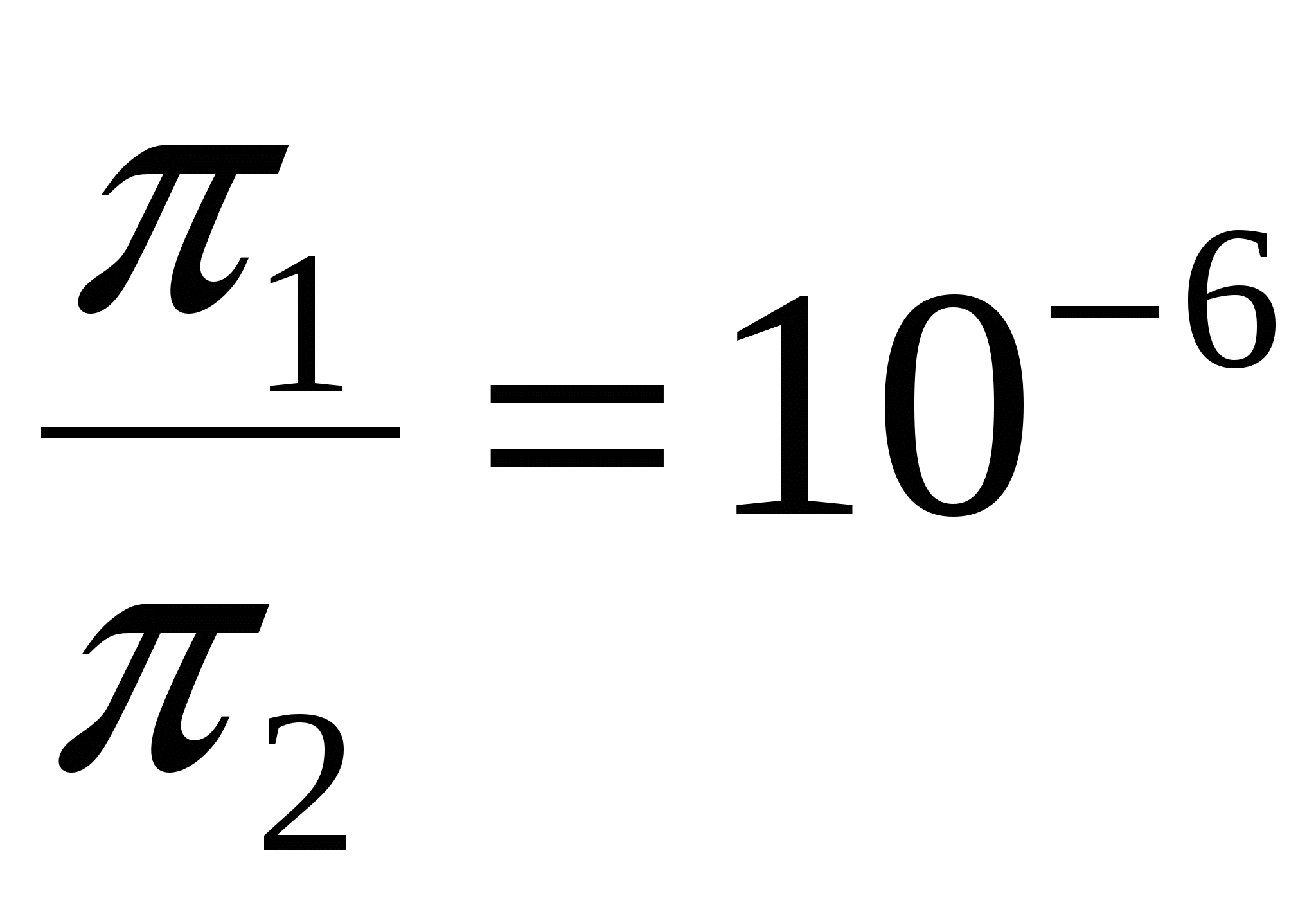
   

В коллоидных системах осмотическое давление много ниже, чем в истинных растворах.

Эндоосмос и эктоосмос: внутрь ограниченного объема; наружу.

Оптические Свойства. Светорассеяние и Светопоглощение.

В зависимости от типа поверхности можно рассматривать следующие ситуации:

1) , плоская поверхность – зеркальное отражение

2) , искривленная поверхность – дифракция, интерференция

3) - рассеяние

Для коллоидных систем характерно релеевское светорассеяние.

Условия:

1.

2. изотропная среда

3. «белый золь»: а) частицы не окрашены; б) частицы не электропроводны; в) сферическая форма.

4. концентрация мала

5. объем системы мал.

Световой поток с напряженностью возбуждает в частицах дисперсной фазы дипольный момент (), в результате частица рассматривается как суммарный асциллирующий диполь. Рассеянный свет полностью поляризован в плоскости, перпендикулярной к направлению светового луча. При этом в плоскости поляризации существует анизотропия световых волн.

,

- число частиц в м³; V – объем одной частицы; R – расстояние до источника; - длина волны; n, n₀ – показатели преломления ДФ и ДС; I₀ – интенсивность падающего света; - угол между дипольным моментом и направлением рассеянного луча.

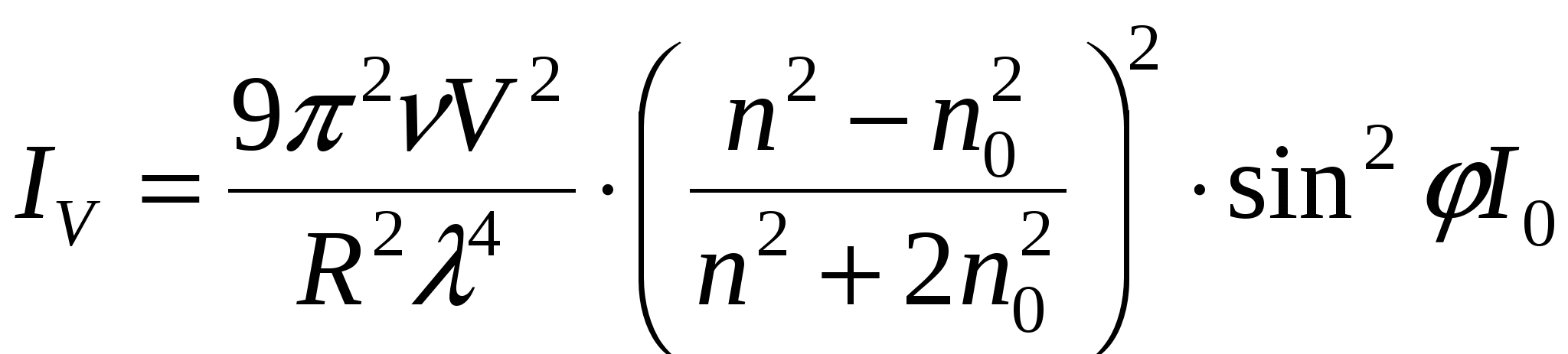При светорассеянии света (световой поток) меняет направление, но не длину волны.







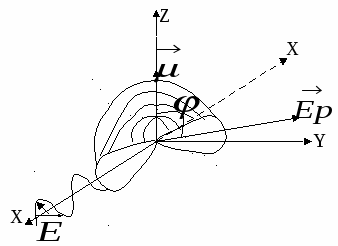
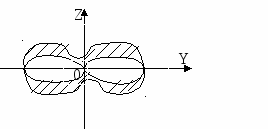
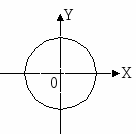
Не заштрихованная часть – неполяризованный свет, заштрихованная – поляризованный.

Сечение фигуры плоскостями yOx и zOy называется индикатрисами светорассеяния (Фигуры Ми).

Закон Релея: .

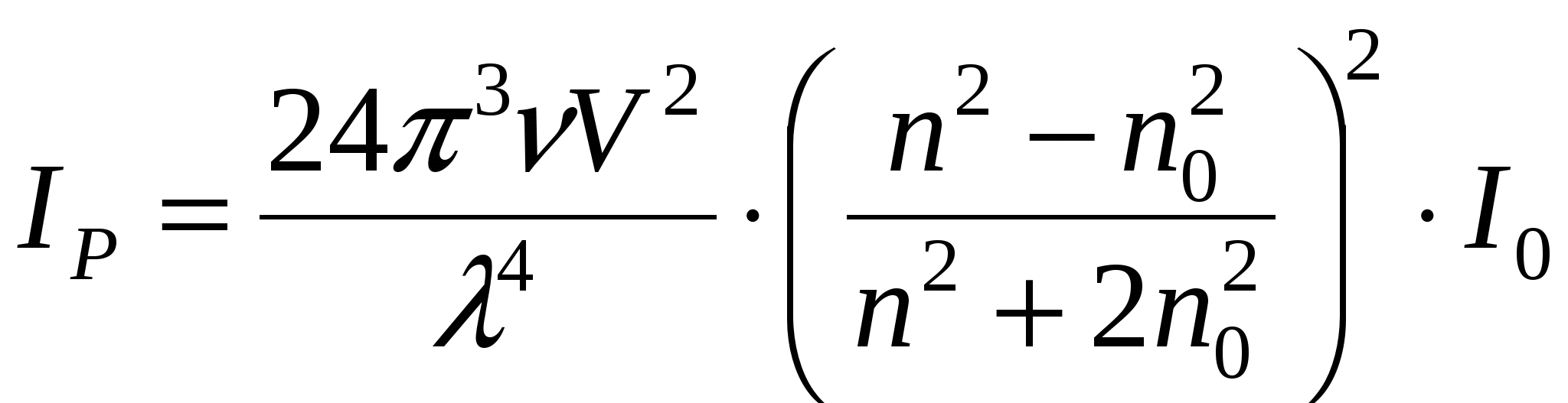Интенсивность рассеянного света пропорциональна числу частиц, их объему и обратно пропорциональна .



Для частиц сложной формы интенсивность рассеянного света I_P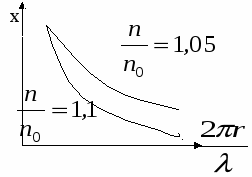




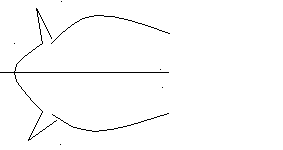
Индикатриса для частиц сложной формы
Светопоглощение.

Интенсивность проходящего света уменьшается на величину интенсивности света рассеянного во всех направлениях. Поэтому интенсивность поглощенного системой света будет зависеть от толщины слоя дисперсной системы через которую прошел свет.





- Закон Бугера-Ламберта-Бера

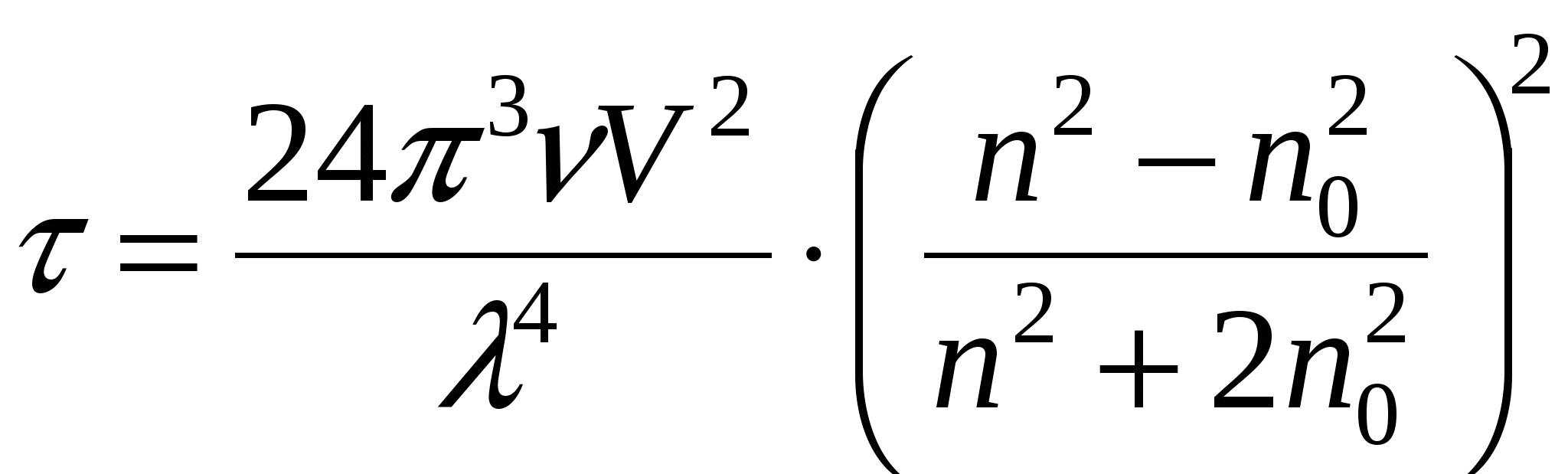- мутность системы [м^-1]

Мутность – это величина, обратная расстоянию, на котором интенсивность падающего света ослабляется в е раз.

Для дисперсных систем окраска растворов – функция от размеров частицы, для молекулярных нет.

Увеличение размера частицы сдвигает максимум светопоглощения в сторону больших длин волн.