Конкурс математических и компьютерных работ школьников Вектор будущего 2007

• Название: Конкурс математических и компьютерных работ школьников Вектор будущего 2007
• Дата: 14.04.2021
• Размер: 202 Kb.
• Имя файла: Metod_matematicheskoy_indukcii__Ego_primenenie_k_resheniyu_algeb.doc
• Тип: Конкурс; #194821

Министерство образования Саратовской области

Саратовский государственный социально - экономический университет

Областной конкурс математических и компьютерных работ школьников

«Вектор будущего – 2007»


«Метод математической индукции.

Его применение к решению алгебраических задач»
(секция «математика»)


Творческая работа

ученицы 10«А» класса

МОУ «Гимназии №1»

Октябрьского района г. Саратова

Арутюнян Гаянэ.


Руководитель работы:

учитель математики

Гришина Ирина Владимировна.

Саратов

2007

Содержание:

Введение…………………………………………………………………………………3

Принцип математической индукции и его

доказательство…………………………………………………………………………..4

Примеры решений задач………………………………………………………………..9

Заключение……………………………………………………………………………..16

Литература………………………...……………………………………………………17

Введение.

Метод математической индукции можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно и подкреплять свою мысль доказательством, проведённым по всем правилам логики.
        В настоящее время выросла область применения метода математической индукции, но в школьной программе ему, к сожалению, отводится мало времени. А ведь это так важно - уметь размышлять индуктивно.

Принцип математической индукции и его доказательство

Обратимся к существу метода математической индукции. Рассмотрим различные утверждения. Их можно подразделить на общие и частные .Приведем примеры общих утверждений .

Все граждане России имеют право на образование.

Во всяком параллелограмме диагонали в точке пересечения делятся пополам.

Все числа, оканчивающиеся нулем, делятся на 5 .

Соответствующие примеры частных утверждений:

Петров имеет право на образование.

В параллелограмме ABCD диагонали в точке пересечения делятся пополам.

140 делится на 5.

Переход от общих утверждений к частным называется дедукцией (от латинского deductio- вывод по правилам логики).

Рассмотрим пример дедуктивного вывода.

Все граждане России имеют право на образование. (1)

Петров – гражданин России. (2)

Петров имеет право на образование. (3)

Из общего утверждения (1) при помощи (2) получено частное утверждение (3).

Обратный переход от частных утверждений к общим называется индукцией (от латинского inductio- наведение).

Индукция может привести как к верным, так и к неверным выводам.

Поясним это двумя примерами.

140 делится на 5. (1)

Все числа, оканчивающиеся нулем, делятся на 5 . (2)

140 делится на 5. (1)

Все трехзначные числа делятся на 5. (2)

Из частного утверждения (1) получено общее утверждение (2). Утверждение (2) верно.

Второй пример показывает, как из частного утверждения (1) может быть получено общее утверждение (3) , притом утверждение (3) не является верным.

Зададимся вопросом, как пользоваться в математике индукцией, чтобы получать только верные выводы. Рассмотрим несколько примеров индукции, недопустимой в математике.

Пример 1.

Рассмотрим квадратный трехчлен следующего вида Р(x)= x² + x + 41, на который обратил внимание еще Леонард Эйлер.

Р(0) = 41, Р(1) = 43, Р(2) = 47, Р(3) = 53, Р(4) = 61, Р(5) = 71, Р(6) = 83, Р(7) = 97, Р(8) = 113, Р(9)=131, Р(10) = 151.

Мы видим, что всякий раз значение трехчлена - простое число. На основании полученных результатов утверждаем, что при подстановке в рассматриваемый трехчлен вместо x любого целого неотрицательного числа всегда в результате получается простое число.

Однако сделанный вывод не может считаться достоверным. В чем же дело? Дело в том, что в рассуждениях высказаны общие утверждения относительно любого х только на основании того, что это утверждение оказалось справедливым для некоторых значений х.

В самом деле, при более внимательном изучении трехчлена Р(х) числа Р(0), Р(1), …, Р(39) - простые числа , но Р(40) = 41² – составное число. И совсем явно: Р(41) = 41² +41+41 кратно 41.

В этом примере мы встретились с утверждением, справедливым в 40 частных случаях и все же вообще оказавшимся несправедливым.

Рассмотрим еще несколько примеров.
Пример 2.

В 17 веке В.Г. Лейбниц доказал, что при всяком натуральном n числа вида n³ — n кратны 3, n⁵ — n кратны 5, n⁷ — n кратны 7. На основании этого, он предложил, что при всяком нечетном k и натуральном n число n^k— n кратно k , но скоро сам заметил, что 2⁹ –2=510, которое, очевидно, не делится на 9 .

Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще.

Естественно возникает вопрос: имеется утверждение, справедливое в нескольких частных случаях; все частные случаи рассмотреть невозможно; как же узнать, справедливо ли это утверждение вообще?

Этот вопрос иногда удается решить посредством применения особого метода рассуждений, называемого методом математической индукции. В основе этого метода лежит принцип математической индукции, заключенный в следующем: утверждение справедливо для любого натурального n , если:

1. 
   оно справедливо для n= 1;
   
2. 
   из справедливости утверждения для какого-то произвольного натурального n=k , следует его справедливость для n= k+1.
   

Доказательство.

Предположим противное, то есть пусть утверждение справедливо не для всякого натурального n. Тогда существует такое натуральное число m, что

1. 
   утверждение для n=m несправедливо,
   
2. 
   для всех n

Очевидно, что m>1, так как при n=1 утверждение справедливо (условие 1). Следовательно, m—1 - натуральное число. Для натурального числа m—1 утверждение справедливо, а для следующего натурального числа m оно несправедливо. Это противоречит условию 2. Полученное противоречие показывает неверность предположения. Следовательно, утверждение справедливо для всякого натурального n, ч. т. д.

Доказательство, основанное на принципе математической индукции, называется доказательством методом математической индукции. Такое доказательство должно состоять из двух частей, из доказательства двух самостоятельных теорем.

Теорема 1. Утверждение справедливо для n=1.

Теорема 2. Утверждение справедливо для n=k+1, если оно справедливо для n=k, где k-произвольное натуральное число.

Если обе эти теоремы доказаны, то на основании принципа математической индукции утверждение справедливо для любого
натурального n.

Необходимо подчеркнуть, что доказательство методом математической индукции, безусловно, требует доказательства обеих теорем 1 и 2. Пренебрежительное отношение к теореме 2 приводит к неверным выводам (примеры 1-2). Покажем на примере, сколь обязательно доказательство теоремы 1.

Пример 3. «Теорема»: всякое натуральное число равно следующему за ним натуральному числу.

Доказательство проведем методом математической индукции.

Предположим, что k=k+1 (1).

Докажем, что k+1=k+2 (2). Для этого к каждой части «равенства» (1) прибавим 1.Получаем «равенство» (2). Выходит, что если утверждение справедливо для n=k, то оно справедливо и для n=k+1., ч.т.д.

Очевидное «следствие» из «теоремы»: все натуральные числа равны.

Ошибка заключается в том, что теорема 1, необходимая для применения принципа математической индукции не доказана и не верна, а доказана только вторая теорема.

Теоремы 1 и 2 имеют особое значение.

Теорема 1 создает базу для проведения индукции. Теорема 2 дает право неограниченного автоматического расширения этой базы, право перехода от данного частного случая к следующему, от n к n+1.

Если не доказана теорема 1 , а доказана теорема 2 , то, следовательно, не создана база для проведения индукции, и тогда бессмысленно применять теорему 2 ,так как и расширять-то, собственно, нечего.

Если не доказана теорема 2 , а доказана только теорема 1, то, хотя база для проведения индукции и создана, право расширения этой базы отсутствует.

Замечания.

1. 
   Иногда вторая часть доказательства опирается на справедливость утверждения не только для n=k, но и для n=k-1. В этом случае утверждение в первой части должно быть проверено для двух последующих значений n.
   
2. 
   Иногда утверждение доказывается не для всякого натурального n, а для n > m, где m – некоторое целое число. В этом случае в первой части доказательства утверждение проверяется для n=m+1, а если это необходимо, то для нескольких последующих значений n.
   

Подытожив сказанное, имеем: метод математической индукции позволяет в поисках общего закона испытывать возникающие при этом гипотезы, отбрасывать ложные и утверждать истинные.

Далее отметим отличия математической индукции от понимания индукции в широком смысле слова.

Всем известна роль процессов обобщения результатов отдельных наблюдений и опытов (т.е. индукции) для эмпирических, экспериментальных наук. Математика же издавна считалась классическим образцом осуществления чисто дедуктивных методов, так как явно или неявно всегда подразумевается, что все математические предложения (кроме принятых за исходные - аксиом) доказываются, а конкретные применения этих предложений выводятся из доказательств, пригодных для общих случаев (дедукция).

Что же значит индукция в математике? Следует ли ее понимать как не вполне надежный способ, и как искать критерий надежности таких индуктивных методов? Или достоверность математических заключений той же природы, что и опытные обобщения экспериментальных наук, таких, что любой доказанный факт неплохо было бы еще и «проверить»? В действительности дело обстоит не так.

Индукции (наведение) на гипотезу играет в математике очень большую, но чисто эвристическую роль: она позволяет догадываться, каким должно быть решение. Но устанавливаются же математические предложения только дедуктивно. И метод математической индукции есть чисто дедуктивный метод доказательства. В самом деле, доказательство, проводимое этим методом, состоит из двух частей:

1. 
   так называемый «базис» – дедуктивное доказательство искомого предложения для одного (или нескольких) натурального числа;
   
2. 
   индукционный шаг, состоящий в дедуктивном доказательстве общего утверждения. Теорема именно доказывается для всех натуральных чисел. Из базиса, доказанного, например, для числа 0, мы получаем, по индукционному шагу, доказательство для числа 1, затем таким же образом для 2, для 3 …- и так утверждение может быть обосновано для любого натурального числа.
   

Иначе говоря, название «математическая индукция» обусловлено тем, что этот метод просто ассоциируется в нашем сознании с традиционными индуктивными умозаключениями (ведь базис действительно доказывается только для частного случая); индукционный шаг, в отличие от основанных на опыте критериев правдоподобности индуктивных умозаключений в естественных и общественных науках, есть общее утверждение, не нуждающееся ни в какой частной посылке и доказываемое по строгим канонам дедуктивных рассуждений. Поэтому математическую индукцию называют «полной» или «совершенной», так как она есть дедуктивный, совершенно надежный метод доказательства.

Примеры решений задач

Индукция в алгебре

Рассмотрим несколько примеров алгебраических задач, а также доказательство различных неравенств, решаемых с применением метода математической индукции.

Задача 1. Угадать формулу для суммы и доказать её.

А(n)= 2 1² + 32² + …..+(n+1) n².

Решение.

1. Преобразуем выражение для суммы А(n):

A(n)= 21² + 32² + ….+ (n+1) n² = (1+1) 1² + (2+1) 2² + …. + (n+1) n²= =11² + 22² + …+nn² + 1² + 2² +… +n² =1³ + 2³ +… +n³+1² + 2² +… +n²= В(n) + C(n), где B(n) = 1³ + 2³+ …..+ n³, C(n)= 1² + 2² +…+ n².

2. Рассмотрим суммы C(n) и B(n).

а) С(n) = 1² + 2² +…+ n². Одна из часто встречающихся задач на метод математической индукции, доказать, что для любого натурального n , выполняется равенство

1² + 2² +…+ n² = (1)

Предположим, что (1) верно при всех nN.

б) B(n) = 1³ + 2³+ …..+ n³ . Пронаблюдаем, как изменяются значения B(n) в зависимости от n .

B(1) = 1³ = 1 .

B(2) = 1³ + 2³ = 9 = 3² = ( 1 + 2 )²

B(3) = 1³+ 2³+ 3³ = 36 =

Таким образом, можно предположить, что
B(n) = (1 + 2 + ….+ n)² = (2)

в) В результате для суммы А(n) получаем

А(n) = =

= (*)

3. Докажем полученную формулу (*) методом математической индукции.

а) проверим справедливость равенства (*) при n = 1.

А(1) = 2 =2,

Очевидно, что формула (*) при n= 1 верна.

б) предположим, что формула (*) верна при n=k , где kN, то есть выполняется равенство

A(k)=

Исходя из предположения, докажем справедливость формулы при n=k+1. Действительно,

A(k+1)=

=

=

Так как формула (*) верна при n=1, и из предположения, что она верна при некотором натуральном k, следует ее справедливость при n=k+1, на основании принципа математической индукции заключаем, что равенство


выполняется при всяком натуральном n.

Задача 2.

Вычислить сумму 1—2 + 3—4 +…(—1)^n-1n.

Решение.

1. 
   Выпишем последовательно значения сумм при различных значениях n.
   

A(1)=1, A(2)=1—2= —1, A(3)=1—2+3=2, A(4)=1—2+3—4= —2,

A(5)=1—2+3—4+5=3, A(6)=1—2+3—4+5—6= —3.

Наблюдая закономерность, можем предположить, что A(n)= — при 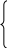четных n и A(n)= при нечетных n. Объединим оба результата в единую формулу:

A(n) = , где r – остаток от деления n на 2.

И r, очевидно, определяется следующим правилом

0, если n – чётное,

r =

1, если n – нечётное.
Тогда r (можно догадаться) представимо в виде:

Окончательно получим формулу для A(n):

A(n)=

(*)
Докажем выполнение равенства (*) при всех nNметодом математической индукции.

2. а) Проверим равенство (*) при n=1. А(1) = 1=

Равенство справедливо

б) Предположим, что равенство

1—2+3—4+…+(—1)^n—1 n =

верно при n=k. Докажем, что оно справедливо и при n=k+1, то есть

A(k+1)=

В самом деле,

A(k+1)=A(k)+(—1)^k(k+1) =

=

=

Что и требовалось доказать.

Метод математической индукции применяется также для решения задач на делимость.

Задача 3.

Доказать, что число N(n)=n³ + 5n делится на 6 при любом натуральном n.

Доказательство.

1. 
   При n=1 число N(1)=6 и потому утверждение справедливо.
   
2. 
   Пусть при некотором натуральном k число N(k)=k³+5k делится на 6. Докажем, что N(k+1)= (k+1)³ + 5(k+1) делится на 6. Действительно, имеем
   N(k+1)= (k+1)³ + 5(k+1)=(k³+5k)+3k(k+1)+6.
   

Поскольку k и k+1 — рядом стоящие натуральные числа, то одно из них обязательно четно, поэтому выражение 3k(k+1) делится на 6. Таким образом, получаем, что N(k+1) также делится на 6. Вывод число N(n)=n³ + 5n делится на 6 при любом натуральном n.

Рассмотрим решение более сложной задачи на делимость, когда метод полной математической индукции приходится применять несколько раз.

Задача 4.

Доказать, что при любом натуральном n число не делится нацело на число 2ⁿ⁺³.

Доказательство.

1. 
   При n=1 утверждение очевидно, так как 8 не делится на 16.
   
2. 
   Предположим теперь, что утверждение справедливо при n=k, т.е. число не делится нацело на 2^k+3. Докажем тогда, что число не делится нацело на число 2^k+4
   

Представим в виде произведения =

= (*)
По предположению первый множитель в (*) не делится нацело на число 2^k+3, то есть в представлении составного числа в виде произведения простых чисел число 2 повторяется не более чем (k+2) раза. Таким образом, чтобы доказать, что число не делится нацело на 2^k+4, надо доказать, что не делится на 4.

Для доказательства этого утверждения докажем вспомогательное утверждение: для любого натурального n число 3²ⁿ +1 не делится на 4. Для n=1 утверждение очевидно, так как 10 не делится на 4 без остатка. При предположении, что 3^2k+1 не делится на 4, докажем, что и 3^2(k+1)+1 не делится
на 4. Представим последнее выражение в виде суммы:

3^2(k+1)+1=3^2k+2+1=3^2k_*9+1=(3^2k+1)+8_*3^2k. Второе слагаемое суммы делится на 4 нацело, а первое не делится. Следовательно, вся сумма не делится на 4 без остатка. Вспомогательное утверждение доказано.

Теперь ясно, что не делится на 4, так как число 2^k является четным числом.

Окончательно получаем, что число не делится нацело на число 2ⁿ⁺³ ни при каком натуральном n.

Рассмотрим теперь пример применения индукции к доказательству неравенств.

Задача 5.

При каких натуральных n справедливо неравенство 2ⁿ > 2n + 1?

Решение.

1. При n=1 2¹ < 2*1+1,

при n=2 2² < 2*2+1,

при n=3 2³ > 2*3+1,

при n=4 2⁴ > 2*4+1.

По-видимому, неравенство справедливо при любом натуральном n3. Докажем это утверждение.

2. При n=3 справедливость неравенства уже показана. Пусть теперь неравенство справедливо при n=k, где k — некоторое натуральное число, не меньшее 3, т.е.

2^k > 2k+1 (*)

Докажем, что тогда неравенство справедливо и при n=k+1, то есть 2^k+1>2(k+1)+1. Умножим (*) на 2, получим 2^k+1>4k+2. Сравним выражения 2(k+1)+1 и 4k+2.

4k+2—(2(k+1)+1)=2k—1. Очевидно, что 2k—1>0 при любом натуральном k. Тогда 4k+2>2(k+1)+1, т.е. 2^k+1>2(k+1)+1. Утверждение доказано.

Задача 6.

Неравенство для среднего арифметического и среднего геометрического n неотрицательных чисел (неравенство Коши).
Если , ,…, - любые неотрицательные числа, то

(*)
Равенство имеет место лишь при =
Доказательство.

1. 
   При n=2 неравенство справедливо
   

- это неравенство является следствием очевидного неравенства:

2. 
   Предположим, что неравенство верно при n=k; докажем, что оно будет верным и при n=2k.
   

Действительно,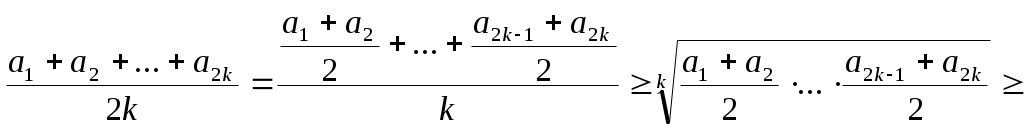


=
Так как неравенство (*) имеет место при n=2, то оно будет выполняться для n=4, 8,16… и т.д., то есть, вообще, для всякого n= (p=1,2,3,…)

3. 
   Пусть теперь n-произвольное натуральное число. Если n , то найдём такое натуральное число s, что n+s= . Тогда для любых неотрицательных чисел , согласно доказанному, справедливо неравенство:
   

Положим в этом неравенстве 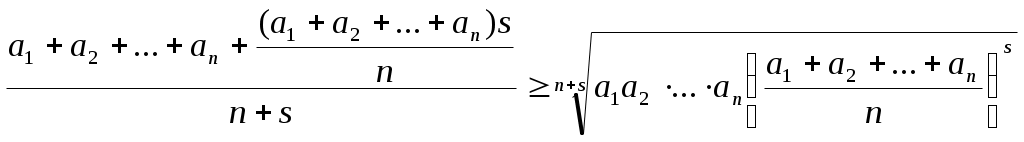, получим

, откуда, обозначив , будем иметь

, найдём, что

Возведём обе части последнего неравенства в степень (n+s), получим

, откуда следует, что , т.е. , или
Покажем, что в неравенстве (*) равенство имеет место в том и только в том случае, если = .

Ясно, что если 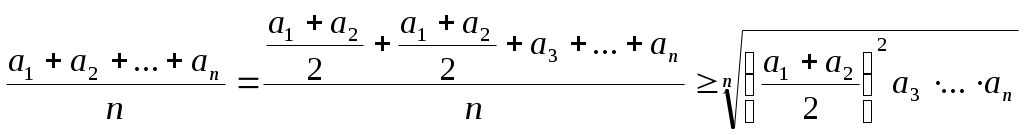= , то соотношение (*) превращается в равенство. Докажем, что если хотя бы два из этих чисел не равны между собой, то в (*) левая и правая части не равны между собой. Пусть . Тогда

Так как 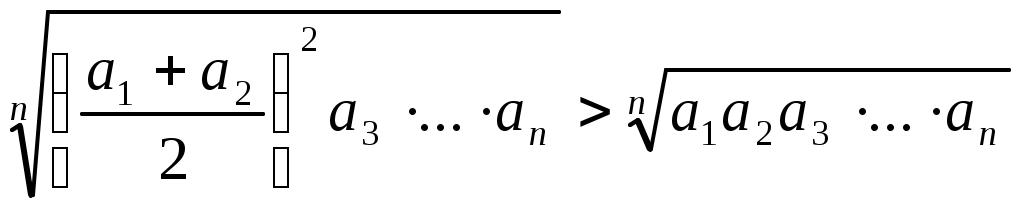, то , следовательно,

, а потому (**)

Если хотя бы одно из чисел равно нулю, то неравенство (**) также справедливо.

Заключение.

При выполнении работы я изучила суть метода математической индукции и его доказательство. В работе представлены задачи, в которых большую роль сыграла неполная индукция, наводящая на правильное решение, и затем проведено доказательство, полученное с помощью метода математической индукции.

Литература.

1. 
   Болтянский В.Г., Сидоров Ю.В., Шабурин М.И. Лекции и задачи по элементарной математике; Наука, 1974.
   
2. 
   Виленкин Н.Я. , Шварцбурд С.И. Математический анализ.—
   М.: Просвещение, 1973.
   
3. 
   Галицкий М.Л., Мошкович М.М, Шварцбурд С.И. Углубленное изучение курса алгебры и математического анализа.— М.: Просвещение, 1990.
   
4. 
   Потапов М.К., Александров В.В., Пасиченко П.И. Алгебра и анализ элементарных функций.— М.: Наука, 1980.
   
5. 
   Соминский И.С., Головина М.Л., Яглом И.М. О математической индукции.— М.: Наука, 1967.