Суровый конспект. Конспект лекций курса Теория и расчет измерительных приборов и систем
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
12.6 Метод относительных погрешностей.В некоторых случаях функция преобразования измерительного устройства выражается произведением нескольких множителей и является постоянной величиной, не зависящей от изменения входной величины. Для таких случаев может быть применён метод относительных погрешностей. Механизмы, состоящие из рычагов или фрикционных передач, нередко исследуют и рассчитывают, используя понятие об относительной погрешности. Различают два вида относительных погрешностей: радиальная погрешность и тангенциальная погрешность. Относительной радиальной погрешностью называют частное от деления абсолютного отклонения радиального размера на номинальное значение этого размера. Для относительной радиальной погрешности характерно то обстоятельство, что в последовательной передаче, в независимости от принадлежности отклонения к любому звену, погрешность имеет постоянный коэффициент влияния ±1. Выходные параметры многих преобразовательных элементов измерительных устройств выражаются сложной степенной зависимостью через величины его отдельных параметров: пружины, мембранные коробки, сильфоны, индуктивные преобразователи и т.д. Выходной сигнал: 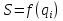 . .Относительная ошибка: 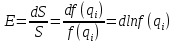 , т.е. относительная ошибка функции равна дифференциалу натурального логарифма этой функции. Аналогично, что если функция зависит от нескольких параметров, то максимальное значение относительной ошибки результата равно полному дифференциалу натурального логарифма функции, причём при вычислении дифференциала следует брать сумму абсолютных значений дифференциалов всех членов логарифма (т.е. все частные ошибки складываются). , т.е. относительная ошибка функции равна дифференциалу натурального логарифма этой функции. Аналогично, что если функция зависит от нескольких параметров, то максимальное значение относительной ошибки результата равно полному дифференциалу натурального логарифма функции, причём при вычислении дифференциала следует брать сумму абсолютных значений дифференциалов всех членов логарифма (т.е. все частные ошибки складываются).Пример: расчёт усилия винтовых цилиндрических пружин производится по формуле: 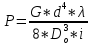 P- осевое усилие пружины. G- модуль сдвига материала. d- диаметр проволоки. λ- ход пружины. Do-средний диаметр, D- наружный диаметр пружины. i – число рабочих витков пружины. 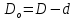 Находим натуральный логарифм P: 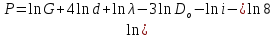 Находим дифференциал этого выражения: причём в правой части берём сумму абсолютных значений его членов 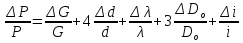 Учитывая вероятностный характер проявления первичных погрешностей, суммарную относительную погрешность осевого усилия пружины находят квадратическим сложением членов приведенного выражения: 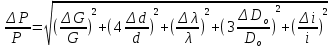 12.7 Метод плеча и линии действия.Данный метод разработан профессором Н.А. Калашниковым, в созданной им теории реальных механизмов, применительно, главным образом, к механизмам с высшими парами (зубчатые, кулачковые и другие). По этой теории погрешности механизма можно представить как приращение обобщенного плеча, перпендикулярного к линии действия некоторой обобщенной силы. Метод предназначен для определения суммарной погрешности. Недостаток: метод пригоден для исследования только механизмов. Суть метода: при исследовании реальных механизмов по Калашникову, любой механизм представляют как совокупность простейших. За прототип простейшего механизм принимают линию действия и соответствующие ей плечи (плечо). Линия действия – линия, по которой передаётся действие элементов звеньев. Плечо – перпендикуляр, опущенный из оси вращения звена на соответствующую линию действия. Различают погрешности, возникающие в процессе изготовления и эксплуатации механизма, которые вызывают общее избыточное приращение по линии действия, состоящее из трёх составляющих. 1.∆Fr – приращение, вызванное избыточным изменением обобщенного плеча в следствии нарушения процесса образования рабочей поверхности и из-за погрешностей подвижных звеньев механизма. 2.∆Fл.д. – приращение, создаваемое погрешностями, направленными по линии действия или параллельно ей. 3.∆Fн.з. – приращение, создаваемое погрешностями неподвижных звеньев механизма. 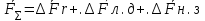 13. Влияние векторных первичных погрешностей на показания измерительного устройства.Векторными первичными погрешностями называются погрешности, характеризуемые некоторым направлением и некоторым числовым значением. Они выражают первичные погрешности относительного положения геометрических элементов в звеньях и кинематических парах и относятся только к нулевым параметрам механизма, то есть к таким, номинальные размеры которых до образования первичной погрешности равны нулю. Эти параметры существуют в механизме, как бы потенциально, проявляясь только в момент образования ошибки. Механизмы бывают плоские и пространственные. Первичная погрешность может возникать в плоскости его движения (первичные погрешности эксцентриситета или плоского переноса) и не в плоскости его движения (пространственного переноса). Векторные первичные погрешности образуются из ошибок в технических условиях на изготовление и сборку механизма. Все векторные первичные погрешности можно свести к двум группам: 1.погрешности эксцентриситетов и перекосов геометрических элементов в звеньях. 2.погрешности эксцентриситетов и перекосов в кинематических парах. Для векторных погрешностей характерно не только непостоянство модулей, но и непостоянство их направлений, что делает весьма затруднительным регулирование этих погрешностей. Каждую плоскую векторную погрешность можно пересчитать в одну или две скалярные первичные погрешности. В одну – проецируя её на линию действия сил. В две – находя составляющие по осям звеньев или же линиям движения точек по ним. Любая векторная погрешность пространственного перекоса может быть пересчитана в две скалярные первичные погрешности, для этого она должна быть переведена в плоскость движения механизма. Для этого используется множитель, равный косинусу угла, составленного направлением первичной погрешности с плоскостью движения механизма. Вследствие случайности модуля и направления векторной первичной погрешности она пересчитывается в случайные скалярные первичные погрешности. В зависимости от требуемой точности расчёта векторную первичную погрешность можно представить в виде: 1. максимальной первичной погрешности, принимая для неё наиболее неблагоприятные направления по линии движения одной из точек для данного положения механизма; 2. некоторого среднего значения первичной погрешности, полученного с помощью теории вероятности, если функция распределения направления векторной первичной погрешности и ее величина известны или гипотетически предполагаются. 14. Погрешности механизма, вызванные неточностью направляющих. На долю направляющих приходится около половины всех кинематических пар механизмов. Поэтому рассмотрение способов учета влияния неточностей направляющих на погрешность движения направляемых звеньев является весьма актуальным. Действие направляющих может быть основано на взаимном скольжении, качении или упругой деформации деталей направляющих устройств. По характеру возможных движений направляющие делятся на вращательные и поступательные. 14.1 Учет влияния зазора во вращательной паре. При наличии зазора шейка шарнира и отверстия будут располагаться несоосно. 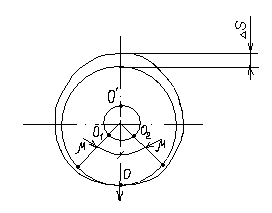 При этом положение подвижного элемента определяется направлением равнодействующей сил, действующих в сочленении. Равнодействующая сил соответствует реакции шарнира и проходит через точку касания обоих элементов пары. В процессе вращательного движения звена изменяется направление действия реакции и, следовательно, перемещается точка соприкосновения элементов шарнира, т.е. происходит взаимное перекатывание соприкасающихся элементов кинематической пары. Для каждого мгновенного положения механизма может быть определена действующая погрешность 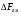 вдоль выходной линии действия, вызванная смещением оси шарнира в пределах зазора. Эта погрешность определяется: вдоль выходной линии действия, вызванная смещением оси шарнира в пределах зазора. Эта погрешность определяется: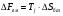 (*) (*)где 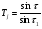 (**) (**)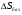 - действующее смещение идеального центра вращения; - действующее смещение идеального центра вращения;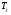 - коэффициент влияния смещения центра; - коэффициент влияния смещения центра;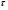 , ,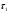 - находятся из схемы преобразованного механизма. - находятся из схемы преобразованного механизма.Формулы (*) и (**) являются универсальными при сохранении требований к дефектному перемещению 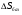 и расстановке углов и расстановке углов 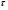 и и 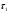 . . Смещение идеального центра вращения направляющей следует рассматривать для трех видов вращательных направляющих:
Для опор скольжения характерным является смещение идеального центра цапфы из центрального положения относительно отверстия на размер 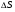 /2, где /2, где 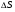 - зазор по направлению действующей реакции. - зазор по направлению действующей реакции. Если при реверсировании работы механизма направление действия реакции отклоняется из-за сил трения на угол 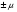 , то вызываемая этим реакция перемещения центра будет определяться: , то вызываемая этим реакция перемещения центра будет определяться: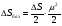 В наихудшем случае, когда не будет иметь место перекатывание (скатывание) центра цапфы из точки 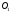 в точку в точку 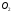 , а при реверсировании механизма центр цапфы будет переходить из точки , а при реверсировании механизма центр цапфы будет переходить из точки 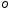 в диаметрально противоположную точку в диаметрально противоположную точку 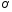 . При этом проекция перемещения центра цапфы равна величине полного зазора: . При этом проекция перемещения центра цапфы равна величине полного зазора: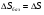 При вращательных направляющих, выполненных на опорах качения, следует принимать во внимание как размер радиального зазора в подшипниках качения 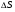 , так и размер радиального биения Е наружного кольца относительно внутреннего. В этом случае размер перемещения звеньев: , так и размер радиального биения Е наружного кольца относительно внутреннего. В этом случае размер перемещения звеньев: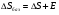 Для вращательных направляющих, выполненных на упругих опорах, следует также учитывать проекции смещения центра поворота в процессе движения звена. При этом можно воспользоваться исследованиями А.Т.Драудина, в которых получены следующие результаты: - для одиночной плоской пружины 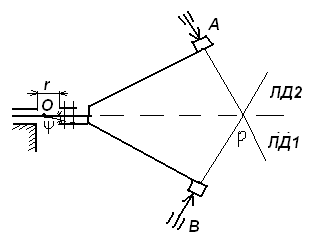 При базовой линии, направленной вдоль оси пружины, проекция смещения идеального центра О при повороте на угол ψот нейтрального положения определяется: 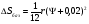 где r – длина свободного участка пружины. - для крестообразного упругого шарнира 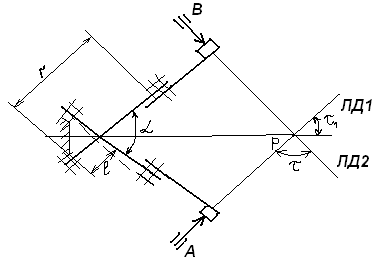 При базовой линии, направленной вдоль оси продольной симметрии, проекция смещения центра на ось продольной симметрии (базовую ось) 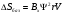 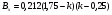 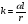 , , 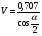 , ,l– большее расстояние от центра О до заделки. При 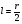 и и 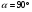 k=1, V=1, следовательно: k=1, V=1, следовательно: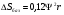 , ,где ψ – угол отклонения от нейтрального положения. 14.2 Учет влияния погрешностей прямолинейных направляющих. При рассмотрении поступательного движения направляемого звена механизма возможны два случая:
1 случай: линии действия пересекаются. В случае, когда линии действия пересекаются в точке Р, особенности рассмотрения проявления погрешностей для поступательных направляющих связаны с тем, что центр мгновенного поворота точка О удален в бесконечность, и базовая линия Р-Р проходит через точку Р, перпендикулярно к траектории идеального движения. С учетом этой особенности могут быть использованы для расчета ранее рассмотренные формулы: 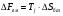 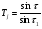 Здесь под 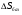 следует понимать погрешность траектории точки Р или любой другой точки, лежащей на нормали Р-Р. следует понимать погрешность траектории точки Р или любой другой точки, лежащей на нормали Р-Р. 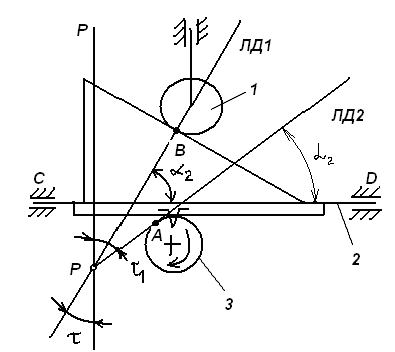 На рисунке показан механизм с поступательно движущимся звеном 2. Это звено снабжено зубчатой рейкой, зацепляющимся в точке А с зубчатым колесом 3, приводящим в движение весь механизм. На звене 2 расположена клиновая линейка, воздействующая в точке В на вертикальный роликовый толкатель 1. Линии действия ЛД1 и ЛД2, проходящие через рабочие точки А и В, пересекаются в точке Р. Базовая линия Р-Р проведена через точку Р, перпендикулярно к траектории движения звена 2. Погрешности направляющих С и D должны быть приведены к дополнительному перемещению 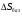 вдоль линии Р-Р. Перемещения должны учитывать при расчете избыточного приращения по выходной линии ЛД2 по известной формуле: вдоль линии Р-Р. Перемещения должны учитывать при расчете избыточного приращения по выходной линии ЛД2 по известной формуле: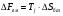 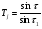 Отметим, что при контроле непрямолинейности хода направляемого звена 2 механизма погрешность 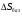 следует измерять по базовой линии Р-Р. следует измерять по базовой линии Р-Р. При расчете погрешности направляющей удобно пользоваться углами, отсчитываемыми между линиями действия и линией движения. 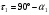 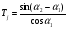 2 случай. Линии действия параллельны. Если линии действия рабочих точек параллельны, то тогда формула 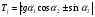 для определения коэффициентов влияния не годна, т.к. 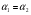 ,следовательно, ,следовательно, 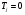 Кроме того не может быть применено и понятие о базовой линии, т.к. не только центр поворота удален в бесконечность, как это было в случае прямолинейного поступательного перемещения, но и отсутствует точка пересечения двух линий действия. Кроме того не может быть применено и понятие о базовой линии, т.к. не только центр поворота удален в бесконечность, как это было в случае прямолинейного поступательного перемещения, но и отсутствует точка пересечения двух линий действия. 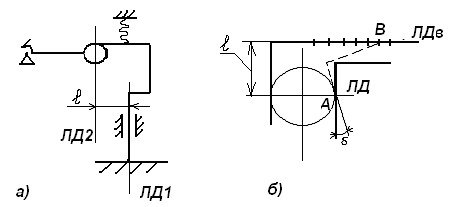 На рис.а показана направляющая для измерительного стержня и рабочей контактной плоскости рычажно-зубчатого индикатора. Рабочая точка А соответствует точке контакта измерительного наконечника с измеряемым изделием, а точка В является точкой соприкосновения плоскости со сферой, закрепленной на качающемся звене рычажного механизма отсчетного прибора. На рис.б показана направляющая в виде штанги и рамки штангенциркуля. Через рабочую точку А проходит линия действия ЛД, а в точке В расположен отсчетный индекс для снятия отсчета по линейной шкале, с которой совпадает и линия движения ЛДв. Возникающая погрешность на выходе вследствие погрешности направляющей пары связано с возникновением перекоса направляемого звена на угол δ и расстоянием l между линиями действия. 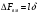 В случае, когда l=0, т.е. линии действия совпадают, имеет место выполнение принципа Аббе, и влияние перекоса направляемого звена становится погрешностью второго порядка малости. Повышение точности работы поступательных направляющих достигается в некоторых случаях путем разделения транспортных и измерительных функций, выполняемых этими направляющими. Обычно в этих случаях в качестве измерительных направляющих используют образцовые поверхности, разгруженные от усилий, связанных с сопротивлениями перемещения кареток. 15. Сетка влияния конечных погрешностей. Это совокупность графиков, показывающих изменение всех конечных погрешностей в зависимости от значения входного сигнала, причем графики для всех конечных погрешностей можно построить в одной или в разных координатных сетках, но обязательно в одинаковом масштабе. Значение каждой конечной погрешности подсчитывается при 3-8 значениях входного сигнала. При построении сетки влияния следует иметь ввиду:
15.1 Анализ сетки влияния первичных погрешностей.
Если 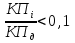 ,то погрешность может быть отнесена к маловлияющей, и можно ее исключить. ,то погрешность может быть отнесена к маловлияющей, и можно ее исключить.Определение ожидаемой суммарной погрешности, т.е. суммирование конечных погрешностей. 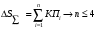 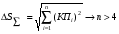
16. Технологическо - эксплуатационный точностной анализ механизмов Данный анализ, главным образом, касается выявления производственных погрешностей изготовления деталей и определения степени их влияния на точность передачи движения механизмом. Он основывается на выбранном технологическом процессе изготовления деталей и должен отвечать на вопросы о том, как связана производственная погрешность размера или формы детали с первичной погрешностью, а допуск с действительным рассеиванием размера детали. Технологическо-эксплуатационный анализ рассматривает также вопросы, связанные с эксплуатацией приборов. Задачами этого анализа являются:
Определение ошибки мертвого хода отнесено к данному анализу потому, что мертвый ход связан с вероятностными величинами зазоров в подвижных сопряжениях, определение которых является предметом технологического точностного анализа, и упругими деформациями звеньев, что непосредственно связано с условиями эксплуатации механизма. 16.1 Технологические составляющие первичных погрешностей механизма К технологическим составляющим первичных погрешностей относятся погрешности изготовления и сборки деталей механизма, вызывающие дополнительные перемещения ведомого звена. Различают следующие виды погрешностей изготовления деталей: погрешности размеров, формы, относительного расположения поверхностей детали, погрешности связанные с шероховатостью. Источником технологических погрешностей изготовления деталей может быть множество причин связанных с оборудованием, режущим и измерительным инструментом, деформациями, изменением твердости обрабатываемой детали, изменением внешних условий. Технологические погрешности в основном случайны. 16.2 Оценка законов распределения технологических первичных погрешностей. Можно указать 3 способа оценки законов распределения производственных погрешностей, два из которых считаются экспериментальными, а один приближенно-табличным. 1-й способ. Заключается в оценке закона распределения технологической погрешности методом математической статистики в условиях реального производства. 2-й способ. Статистическое исследование финишных операций получения параметров. Базируется на предположении, что финишные операции обеспечивают точность измерительного устройства. 3-й способ. Табличный. Используется в проектном расчете. Заключается в использовании опыта предшествующих поколений. Значительные работы в этом направлении выполнены профессором Бородачевым, на основе обследования различных технологических приемов обработки деталей и изучении исследований точности производства, проведенных другими технологами. Им схематизированы разные условия производства, которые приведены к 16-ти типам кривых распределения. Стандартные апроксимации функции распределения случайных составляющих погрешности измерения даны в ГОСТ 8.011. Обычно при ориентировочных расчетах ограничиваются двумя законами:
16.3 Относительные числовые характеристики распределения первичных погрешностей Рассмотрим график рассеяния технологических погрешностей изготовления вала с величиной допуска по чертежу равным 2δ. По оси абсцисс отложены погрешности 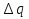 размера вала, а по оси ординат - плотности вероятности рассеяния этих погрешностей, определенные опытным путем. размера вала, а по оси ординат - плотности вероятности рассеяния этих погрешностей, определенные опытным путем. f (x) 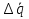 aB x 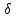 δ δ Δ0 Смещение центра группирования действительного рассеяния размеров относительно середины поля допуска для наружного размера детали равно 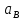 . . Абсолютные характеристики: Профессором Бородачевым были предложены относительные характеристики:
С помощью коэффициента 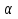 Бородачев связал величину смещения Бородачев связал величину смещения 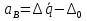 центра группирования отклонения размера детали относительно середины поля допуска с величиной половины допуска. Этот коэффициент служит для определения величины систематической составляющей погрешности изготовления детали, которая равна центра группирования отклонения размера детали относительно середины поля допуска с величиной половины допуска. Этот коэффициент служит для определения величины систематической составляющей погрешности изготовления детали, которая равна 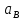 . .
Оба эти коэффициента α, λ зависят от способа обработки и состояния оборудования, а также от симметричности (несимметричности) рассеяния размеров детали относительно середины поля допуска, т.е. α, λ зависят только от вида закона распределения погрешности. 16.4 Законы распределения технологических погрешностей Изучение технологических погрешностей изготовления деталей ведется статистическими методами на основе выявления законов распределения этих погрешностей. Аналитическое выражение закона распределения технологических погрешностей зависит от влияния исходных факторов технологического процесса, изготовления и сборки детали. В случае однородного влияния исходных факторов распределение погрешностей с одной производственной партии подчиняется закону нормального распределения. f (x)   x Рассеяние по закону Гаусса имеет место при следующих условиях возникновения погрешностей:
Однако случайные условия, которые должны сопутствовать возникновению распределения по закону Гаусса, зачастую нарушаются, и могут возникнуть факторы, имеющие доминирующие значения. | ||||||||||||||||||||||

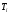
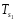
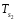
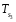
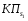
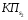
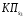
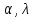 ).
).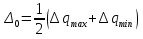
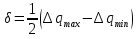
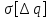
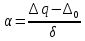 - относительная асимметрия
- относительная асимметрия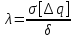 - относительное среднее квадратическое отклонение
- относительное среднее квадратическое отклонение