Суровый конспект. Конспект лекций курса Теория и расчет измерительных приборов и систем
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
|
18.2 Последовательность расчёта точности партии однородных измерительных устройств. 1.Для выбранной схемы прибора определяют погрешности схемы. 2.Выделяют основные устройства и определяют их частные погрешности. 3.Для каждой первичной погрешности находят числовые характеристики, связанные с полем допуска: 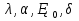 . .4.Вычисляют коэффициент влияния для каждой погрещности. Если коэффициент влияния имеет случайный характер, то для него находят статистические характеристики 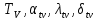 , а также нормируемую корелляционную функцию. r( , а также нормируемую корелляционную функцию. r(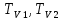 ). ).5.Составляют сводную таблицу расчётных данных для определения результирующей погрешности прибора. 6.По данным таблицы определяют статистические характеристики прибора, например, положения механизма в нескольких положениях ведущего звена при выбранном проценте риска. 7.Для приборов, предназначенных для абсолютных измерений, строят графики значений средних и предельных погрешностей положений механизма в зависимости от положений ведущего звена. 8.Для приборов, применяемых для дифференциальных измерений, определяют статистические характеристики погрешности перемещения механизма в нескольких положениях ведущего звена при выбранном проценте риска. 19.Компенсация погрешностей механизмов. 19.1 Виды конечных погрешностей механизма. Компенсаторами называют специально вводимые в механизм регулировочные устройства, воздействующие на тот или иной его параметр (или же нулевой параметр) для уменьшения его погрешности положения или же перемещения. Процесс введения величин с помощью компенсатора носит название регулирование механизма. Компенсаторы повышают технологичность конструкции, позволяя расширять допуски на изготовление её элементов при сохранении заданной точности прибора. Настройка компенсаторов и регулирование механизма выполняются после его изготовления, следовательно, большинство первичных погрешностей, случайных по характеру их возникновения, проявляются в виде систематических ошибок, и только небольшая их часть, относящаяся к нулевым параметрам механизма, а также предельные погрешности эксплуатационного характера, сохраняют неустойчивый случайный характер. Таким образом, конечные погрешности с точки зрения выбора компенсаторов и системы регулирования механизмов целесообразно делить следующим образом: 1.Конечные погрешности систематического характера. 1.1.Одинаковые по величине или закону их изменения в функции от положения ведущего звена не только для единичного механизма, но и для всех механизмов данного типа. 1.2.Повторяющиеся при многократных действиях каждого конкретного экземпляра механизма, но различны для различных отдельных экземпляров. 2.Конечные случайные погрешности, т.е. такие погрешности, величина или закон изменения которых не повторяются не только в различных экземплярах данного типа, но и при повторных действиях каждого конкретного экземпляра. Конечные погрешности первой группы представляют собой непрерывные функции перемещения ведущего звена. Действие таких погрешностей проявляется по всей шкале прибора, в каждой её точке. Главную часть конечных погрешностей, входящих в эту группу, составляют конечные погрешности в некоторых звеньях, которые практически сохраняют своё постоянство в течение всего периода работы механизма. Конечные погрешности подгруппы 1.1. могут быть уменьшены или вовсе устранены либо путём исправления конструкции, чертежа, размера, либо путём введения в эту конструкцию такого компенсаторного устройства, которое компенсирует как постоянные погрешности (во всех экземплярах механизма), так и погрешности, возникающие в связи с изменением условий эксплуатации механизма. Конечные погрешности подгруппы 1.2. могут быть достаточно полно скомпенсированы, но здесь требуется индивидуальная регулировка каждого конкретного экземпляра механизма. Конечные погрешности 2-ой группы наиболее многочисленны. К ним относятся, главным образом, конечные погрешности, возникающие от первичных погрешностей в нулевых параметрах, но они возникают также и за счёт местных искажений. Они влияют на нестабильность показаний и, как правило, нормируются в приборах наряду с допустимой погрешностью в весьма жёстких пределах. Предупреждение погрешностей этого рода достигается конструктивными средствами, например, такими, как:
19.2 Классификация погрешностей по закономерности их изменения и по способам регулировки 19.2.1 Погрешности постоянные (аддетивные) ΔS Sa So Sb S Так выглядит погрешность начального положения в рычажных механизмах, которая приводит к несимметричности градуировочной характеристики. Погрешность может быть скомпенсирована, для этого вводится постоянный компенсатор. Система регулировки заключается в следующем: с помощью измерительного устройства измеряем любое значение So в пределе от Sa до Sb. Это значение точно соответствует тому, которое необходимо знать в соответствии с градуировочной характеристикой.
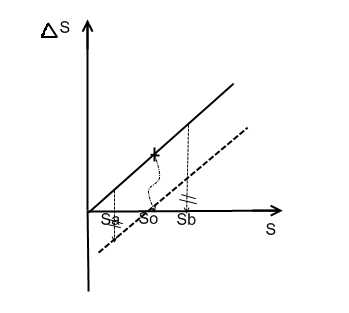 К таким погрешностям относятся все погрешности масштабов, погрешности, вызванные отклонением длин рычагов, отклонения значений электрических сопротивлений. Частичная компенсация погрешности производится введением постоянного компенсатора. Опустив прямую, необходимо сделать ее симметричной относительно оси абсцисс, чем мы максимально уменьшаем значение погрешности по модулю. Для полной компенсации вводится масштабный компенсатор, который в состоянии уменьшить передаточное отношение. Например: изменение длины рычага в аналитических весах. Такой компенсатор позволяет регулировать длины плеч весов. Регулировка осуществляется в двух точках (можно брать 2 любые точки).
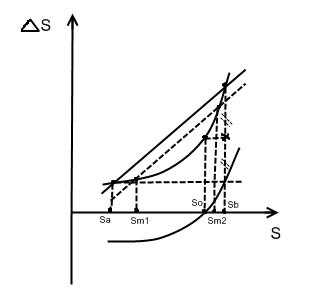 Под нелинейной погрешностью понимается погрешность монотонно убывающая или возрастающая, но изменяющаяся нелинейно. Она частично может быть скомпенсирована введением постоянного компенсатора. Отыскиваем So, для чего делим максимальную ординату пополам, поэтому метод называется половинения погрешности. На практике вводят компенсатор и определяют погрешности по краям шкалы. Когда они становятся равными по краям шкалы и противоположными по знаку, регулировку прекращают. Sm1, Sm2- определяют апроксимирующую прямую Sa =Sm1, Sb =Sm2, т.е. вводят масштабный компенсатор так, чтобы по краям шкалы погрешности были нулевые. Для полной компенсации должен вводиться и третий компенсатор, но на практике обычно обходятся двумя, т.е. компенсация частичная.
ΔS S Так, например, выглядит кинематическая погрешность зубчатых колес. Такие погрешности компенсируются крайне сложно. Для частичной компенсации таких погрешностей необходимо вводить 4 компенсатора, чего на практике никогда не делают. Для борьбы с такими погрешностями вводят искусственные эксцентриситеты зубчатых колес. Для уменьшения конечной суммарной погрешности зубчатые передачи ставят в конце кинематической цепочки, ввиду трудности компенсации.
ΔS S Так обычно выглядит суммарная конечная погрешность. Такую погрешность необходимо представить приближенно в виде многочлена некоторой степени, и в зависимости от вида многочлена вводят соответствующий компенсатор. В заключение отметим, что первичных погрешностей вовсе некомпенсируемых в механизме нет, т.к. компенсаторами являются те же параметры механизма, которые служат источниками первичных погрешностей, а именно: размеры, начальные размеры, начальные положения. Речь может идти лишь о простоте компенсации и ее полноте, что связано с соответствием действия компенсатора той конечной погрешности, которую устраняют. Основная литература 1. Коротков В.П.,Тайц Б.А. Основы метрологии и теории точности измерительных устройств .-М.:Изд-во стандартов, 1988. 2. Грейм И.А. Элементы проектирования и расчет элементов приборов. –Л.: Машиностроение, 1972. 3. Рудзит Я.А., Плуталов В.И. Основы метрологии, точность и надежность в приборостроении. –М.: Машиностроение, 1991. Дополнительная литература 1. Кемпинский М.М. Точность и надежность измерительных приборов. –Л.: Машиностроение, 1972. 2. Иванцов А.И. Основы теории точности измерительных устройств. –М.: Издательство стандартов, 1972. |
