Суровый конспект. Конспект лекций курса Теория и расчет измерительных приборов и систем
 Скачать 0.59 Mb.
|
16.4.1 Закон Максвелла, закон эксцентриситета.f(x) α=-0.28 λ=0.38 x Ему подчиняются все существенно положительные погрешности (эксцентриситет, перенос, биение, погрешность формы). 16.4.2 Закон равномерной плотности или закон равной вероятности.α=0; 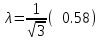 f(x) x Этому закону подчиняются погрешности изготовления угла и погрешности угловой координаты. Начальная фаза векторных погрешностей тоже подчиняется этому закону. 16.4.3 Закон арккосинуса.f(cos(x)) f(sin(x)) α=0 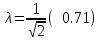 -1 +1 cos(x) sin(x) Этому закону подчиняются функции случайного аргумента cos(x) и sin(x), если случайный аргумент x распределён по закону равномерной плотности. Также этому закону подчиняются коэффициенты влияния векторных погрешностей. 17. Эксплуатационные составляющие первичных погрешностей механизма.Эксплуатационные составляющие первичных погрешностей проявляются в процессе работы механизма. К ним относится: износ поверхностей, силовые и температурные деформации деталей, а так же смещение в зазорах подвижных сопряжений вызванные изменением направления действующих в механизме сил. Эксплуатационные погрешности неподдающиеся расчёту учитываются по опытным данным. 17.1 Влияние износа на точность работы механизма.∆f ∆fэ ∆fпр γ 3 2 1 t Процесс износа можно представить в виде кривой, выражающей количественную зависимость износа ∆f от времени t. Зона 1 графика соответствует начальной стадии износа, в которой происходит интенсивное смятие гребешков микропрофиля поверхности детали. При этом несущая поверхность детали резко увеличивается(в первый момент она составляет около 0,001 от общей опорной геометрической площади).Удельное давление в этот период огромно. Предварительный износ ∆fпр поверхностей происходит при сборке и пробных испытаниях прибора. Он составляет от 20 до 60% от высоты гребешков микропрофиля. Зона 2 соответствует эксплуатационному износу. Зона 3- выходу детали из строя (катастрофический износ). Предварительный износ приводит к увеличению зазора в посадке, поэтому при особо точных расчётах ошибок механизма следует учитывать этот зазор, а также зазор, образующийся вследствие выдавливания смазки между трущимися поверхностями. Для уменьшения эксплуатационного износа принимаются следующие меры: повышение шероховатости для подвижных соединений, выбираются пары антифрикционных материалов, трение скольжение заменяют трением качения, если трущимися материалами являются металлы, то применяют различные смазки. 17.2 Деформации деталей.Наиболее типичными для механизмов приборов являются следующие деформации: от собственного веса, от внутреннего напряжения, от внешней нагрузки и температурная. От собственного веса. Сила веса может вызывать в детали, а, следовательно, и в звене, деформации растяжения, сжатия, изгиба или кручения в зависимости от расположения центра тяжести относительно опор. С точки зрения точности опасны не столько сами деформации, сколько их изменение в процессе работы механизма. Деформации от собственного веса могут стать переменными, если будут изменяться осевые моменты инерции, либо положение центра тяжести звена относительно его опор. В основном учитываются для крупных деталей, а также для деталей характеризующихся значительным выносом центра тяжести от оси вращения (стрелки измерительных приборов). От внутренних напряжений. Внутренние напряжения возникают в процессе изготовления детали, могут быть объёмными (после холодной штамповки, волочения, литья, ковки, сварки, закалки и т.д.) или поверхностными ( после всех операций резания и калибрования). Первые распространяются по всему объёму детали, другие распределяются на небольшой глубине от поверхности. Внутренние напряжения практически не поддаются расчёту, так как неизвестен характер их распределения, но они существуют и вызывают изменение размеров и формы детали. Особенно опасны объёмные деформации от внутренних напряжений, которые могут быть незаметны в процессе изготовления прибора (если цикл изготовления прибора значительно меньше срока старения материала), но они проявляются в период его эксплуатации. Для уменьшения объёмных напряжений следует выбирать материалы с устойчивой структурой и применять искусственное старение материала. Особенно большие внутренние напряжения возникают при закалке. Поэтому детали сложной формы следует подвергать лишь поверхностной закалке или применять другие методы упрочнения поверхности. От внешней нагрузки. Величины этих деформаций можно рассчитать если известен характер изменения нагрузки. В приборных мелкомодульных зубчатых передачах применяют валики небольшого диаметра от 1,5 до 10 мм при крутящем моменте в несколько Н*м, что создаёт соразмерные с общей погрешностью механизма деформации от скручивания валиков, а также изгиба и сдвига штифтов. Существуют способы определения этих деформаций. Для штифтового соединения величина деформации скручивания равна: 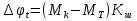 где Кш – коэффициент пропорциональности рад/Н*м, зависит от диаметра валика и максимальной высоты микронеровностей штифтового отверстия. Мк – передаваемый соединением крутящий момент. Мт – момент трения между валиком и ступицей колеса. Температурная деформация Температурные деформации ( 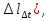 вызванные изменением температуры детали можно определить по формуле: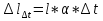 l – размер детали. α – коэффициент линейного расширения детали. ∆t – перепад температур детали. Особенно чувствительны к температурным деформациям такие приборы как: телескопы, измерительные машины, теодалиты, ганиометры. В установившемся тепловом режиме возможны два варианта распределения температуры: 1. постоянна температура, 2. постоянен градиент температуры. Расчёт температурной деформации возможен в обоих случаях. Расчёт температурных деформаций не возможен при неустановившемся тепловом режиме. Тогда задачей конструктора является сведение к минимуму влияния температуры на точность прибора. Этого можно добиться следующими способами: подбор материалов с близкими коэффициентами линейного расширения, оградить детали и весь прибор от температурного влияния окружающей среды (теплоизоляция, термостатирование, экранизация, применение конструктивных температурных компенсаторов). 18. Расчет точности партии однородных измерительных устройств При расчете точности партии изготавливаемых измерительных устройств имеют дело не с конкретными величинами, или же законами изменения первичных погрешностей, а располагают лишь допусками, ограничивающими предельными значениями возможных первичных отклонений элементов прибора. Очевидно, что при сборке деталей механизма все отклонения размеров годных деталей будут находиться в пределах заданных допусков. То же самое относится к динамическим и температурным погрешностям, ограниченным возможными пределами, а внутри этих пределов они могут иметь любое значение. Так как погрешности, действующие в каждом экземпляре прибора и при определенных условиях его использования могут иметь любые значения, лежащие в пределах допуска, то при расчете точности измерительных устройств следует считать эти погрешности случайными величинами (функциями). Суммирование влияния отдельных погрешностей на результирующую точность прибора не должно исходить из алгебраического сложения действия наибольших возможных отклонений, лежащих в границах допуска. Трудно ожидать столь неблагоприятного одновременного сочетания неточностей. В обычных условиях сборки прибора можно ожидать, что в каждый экземпляр прибора попадут детали с отклонениями, лежащими в разных участках полей допуска. Для учета влияния случайного характера погрешностей звеньев механизма необходимо суммировать действие всех отклонений на основе теории вероятности. Сущность этого метода заключается в учете не только значения отклонения, но и вероятности его появления. Это обстоятельство позволяет не учитывать ряд крайних значений, имеющих малую вероятность появления. Следовательно, использование метода теории вероятности дает значение лучше согласующееся с практически наблюдаемыми величинами, чем те значения, которые были найдены при расчете на возможный максимум - минимум погрешности прибора. Основная задача технологического точностного анализа - это учет распределения технологических погрешностей в пределах их полей допусков. Эту задачу можно разбить на несколько частных задач:
Чтобы решить вторую задачу представим суммарную погрешность в следующем виде: 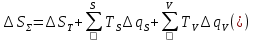 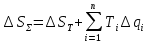 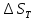 – теоретическая составляющая суммарной погрешности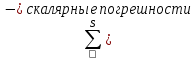 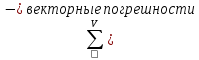 Сделаем следующие допущения:
Закон распределения суммарной погрешности будет нормальным, что следует из первого и двух последних предположений. Рассмотрим еще раз формулу (*) для определения суммарной погрешности.
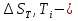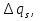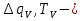 неслучайные величины  случайные величиныСуммарная погрешность представляет собой случайную величину сложной структуры 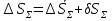 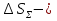 среднее значение суммарной погрешности (систематическая составляющая).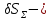 практически предельная случайная составляющая суммарной погрешности.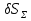 = z 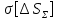 Z- величина, зависящая от процента риска. Процент риска - вероятность получения из годных деталей приборов, имеющих суммарную погрешность, выходящую за расчетные пределы. Найденное таким образом значение суммарной погрешности называется практически предельным полным. Для нахождения пределов для полной погрешности нужно к среднему значению погрешности положения прибавить (отнять) предельную случайную погрешность положения. 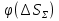 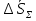 ΔS�� δS�� δS�� ΔS��H ΔS��b Предельные значения определяются соответственно: 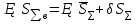 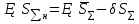 Полученные формулы для определения предельных значений погрешности положения группы механизмов отвечают следующим исходным условиям:
Существенное значение при расчёте точности механизма имеет выбор величины z. φ (Δ 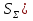 Ф(z) Ф(z) Q/2 Q/2 Zδ Zδ ΔS�� Теоретическая зона рассеивания случайной величины, подчиняющейся нормальному закону распределения, бесконечна, но вероятность получения весьма больших отклонений очень мала. Можно ограничиться практической зоной рассеивания случайной величины, отбрасывая значения с ничтожно малой вероятностью появления. Чем больше значение z, т.е. взята большая зона рассеивания, тем меньше вероятность получения отклонений, выходящих за эту зону. Вероятность этих отклонений, не принимаемых при расчёте, называется процентом риска (Q) и для нормального закона распределе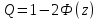ния  , что соответствует сумме двух заштрихованных площадей. Величина 2Ф(z) может быть названа надёжностью расчёта и характеризует вероятность выхода расчётных значений за одну из границ принятой практической зоны рассеивания.При расчёте точности механизма прибора часто z принимают равным 3, т.е. считают ничтожно малой вероятностью выхода случайных погрешностей за каждую из расчётных границ. При этом Q/2=0,13%. В тех случаях, когда при расчёте предельной погрешности прибора расчётное значение её оказывается больше допустимого, можно уменьшить расчётную погрешность механизма. Приняв меньшее значение для z (z=2 вместо 3). Такое уменьшение величины z вызывает увеличение процента риска Q. Подобное повышение при расчёте процента риска может быть допущено, если появление после сборки приборов с погрешностью, превышающей расчётную, может быть обнаружена при их приёмке и не вызывает чрезмерных затруднений при переборке этих приборов. Таким образом, выбор значения z позволяет уменьшить расчётную погрешность положения механизма, увеличивая количество экземпляров приборов, не укладывающихся в расчетные нормы. 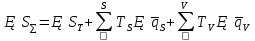 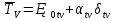 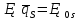 + 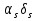 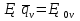+ 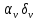 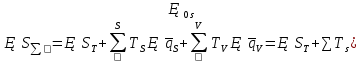+ +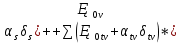 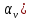Найдя среднее квадратическое отклонение этой величины, определим второе слагаемое из формулы 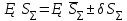 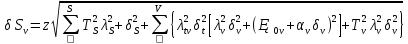 18.1 Способы уменьшения ожидаемой погрешности. Суммарная погрешность зависит от допусков параметров, следовательно, 1-й способ заключается в ужесточении допусков параметров, однако этот способ очень дорог. 2-й способ: уменьшение величины z, т.е. повышение процента риска. Недостатком данного способа является то, что он приводит к удорожанию всей продукции из-за увеличения плана её выпуска. Недостатки обоих способов: 1.Невозможность воздействия на систематическую составляющую суммарной погрешности 2.Удорожание 3-й способ: компенсация конечных погрешностей. Мы отказываемся от полной взаимозаменяемости. В цепь вводятся специальные устройства, называемые компенсаторами, которые позволяют либо непосредственно воздействовать на тот или иной параметр, либо воздействовать на коэффициент влияния, в результате чего уменьшается значение конечных погрешностей. Недостатки способа: 1.Необходимость регулировки. 2.Необходимость усложнения структуры прибора. |
.
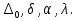
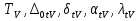