ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г

• Название: Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
• Дата: 24.09.2022
• Размер: 3.24 Mb.
• Имя файла: Лекции по ОТЦ Часть 1.doc
• Тип: Конспект лекций; #693470
• страница: 8 из 8

8. Нелинейные электрические цепи

Нелинейные цепи – это цепи, у которых свойства, параметры зависят от величин токов и напряжений в этих элементах.

Выделяют нелинейное резистивное сопротивление, нелинейную индуктивность и нелинейную емкость.

1. Нелинейные элементы

R 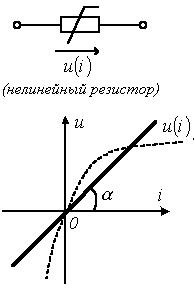=R(i) – управляемый током;

R=R(u) – управляемый напряжением.

- аппроксимация – подбор функции, которая соответствует данному графическому изображению.

Нелинейное резистивное сопротивление характеризуют:

1) статическим сопротивлением в некоторой точке

Технически статическое сопротивление – это сопротивление постоянного тока в какой-то точке.

2) дифференциальным сопротивлением

Технически дифференциальное сопротивление – это сопротивление переменного тока малой амплитуды в какой-то точке.

дифференциальным сопротивлением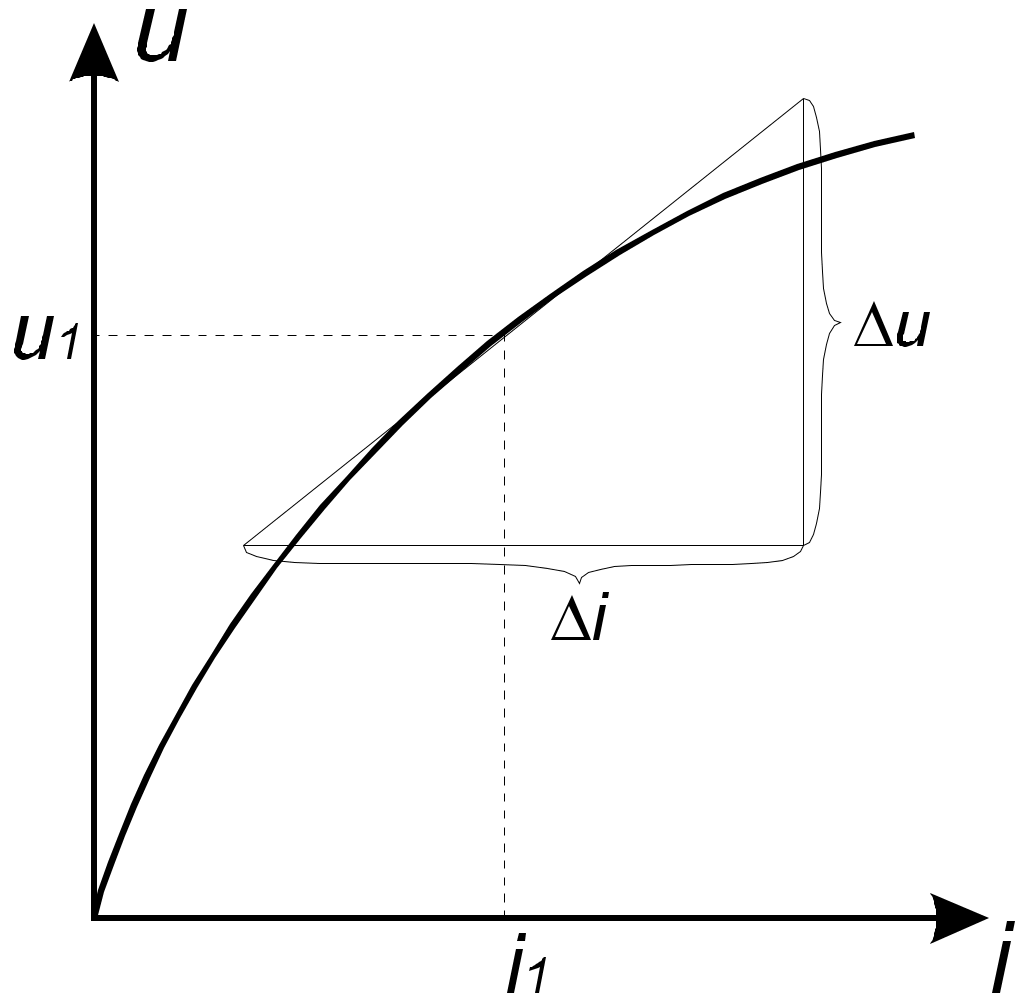

Технически дифференциальное сопротивление – это сопротивление переменному току малой амплитуды в какой-то точке. В общем случае оно не равно статическому.

Аналогичные исследования проводятся для нелинейной индуктивности и емкости.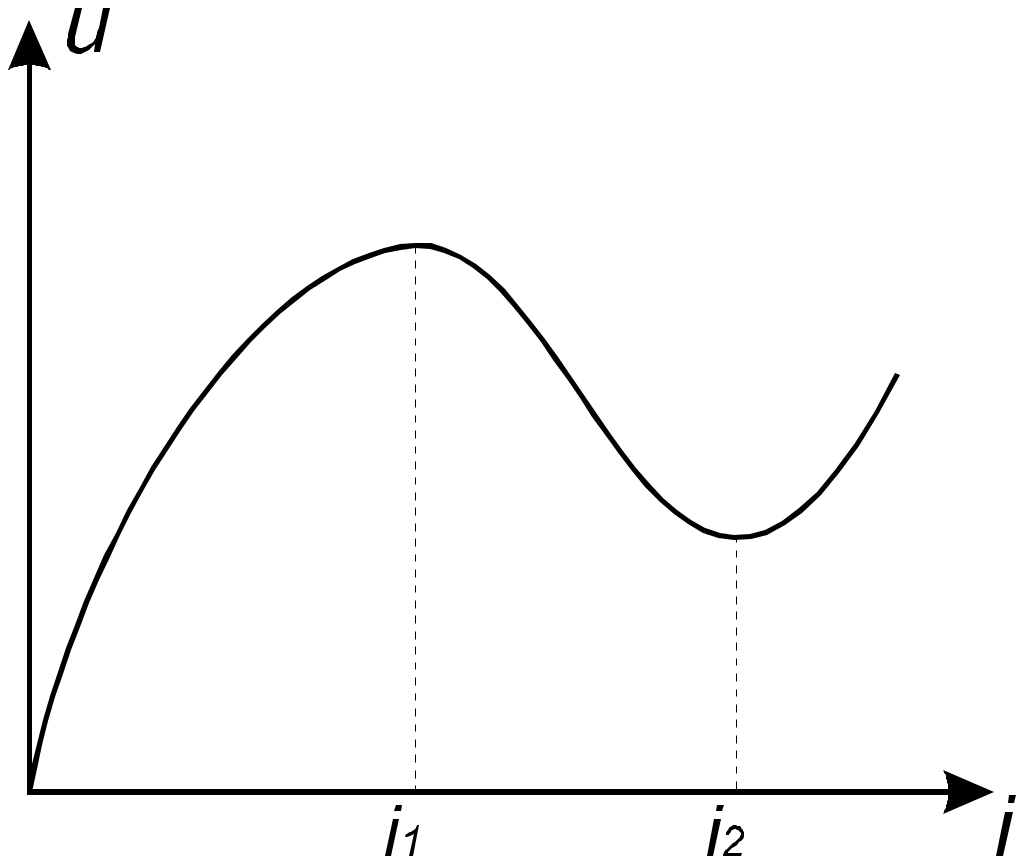

На рис. приведена вольтамперная характеристика нелинейного резистора. При значениях тока i₁  i  i₂ дифференциальное сопротивление будет отрицательным. Мгновенная мощность p = u·i = R_д·i² тоже будет отрицательной, т.е. нелинейный элемент перестает быть пассивным элементом – потребителем энергии, а становится ее источником. Для нелинейных элементов закон Ома справедлив только для статического сопротивления u = R_ст·i.

На практике нелинейные резисторы реализуются полупроводниковыми приборами, а их вольтамперные характеристики снимаются экспериментально.

В ряде задач вольтамперные характеристики нелинейных резисторов требуется описать аналитически. Чаще всего используют полиномы вида

i = a₀ + a₁u + a₂u² + a₃u³ + …


По экспериментальной кривой определяются коэффициенты а₀ , а₁ , а₂ , а₃ ,….

Получение аналитической зависимости по заданной графически характеристике называется аппроксимацией. Рассмотрим в общем виде, как находятся коэффициенты а₀ , а₁ , … в. Ограничим полином (n + 1) членом.

i = a₀ + a₁u + a₂u² + … + a_nuⁿ.


Для определения коэффициентов а_k этого ряда используется метод выбранных точек. Суть его состоит в том, что в выбранном интервале полученный ряд будет совпадать с заданной характеристикой в (n + 1)-й точке. Для этого надо составить n + 1 уравнение, совместное решение которых определяет коэффициенты а_k :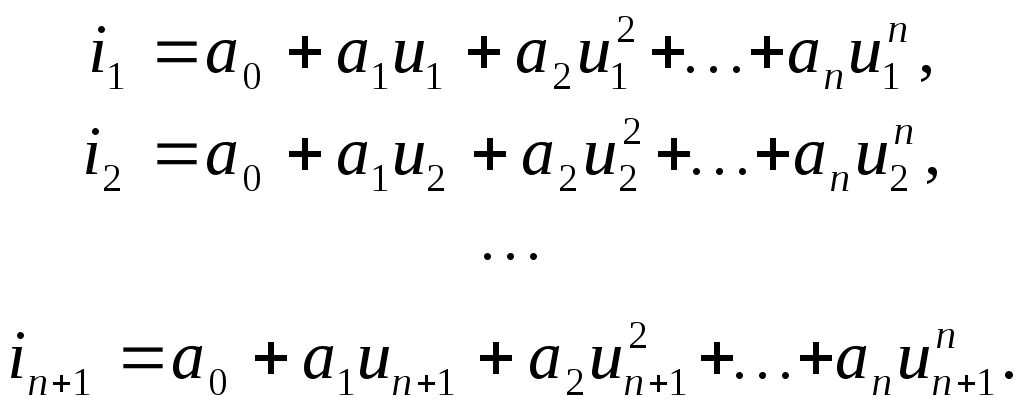



В этих уравнениях i₁ , i₂ , …, i_n+1 – значения токов при напряжениях, соответственно равных u₁ , u₂ , …, u_n+1 , которые берутся из графика заданной характеристики.

Аппроксимация с помощью степенного полинома может быть проведена с достаточно большой точностью. Но для этого потребуется использование полиномов высоких степеней, полученные выражения будут громоздки и неудобны для исследования процессов в нелинейных цепях. Поэтому в зависимости от вида нелинейной характеристики используют полиномы невысоких порядков

Аналогичные исследования проводятся для нелинейной индуктивности и емкости.

2. Расчет цепей с нелинейными элементами
1) Последовательное соединение

При последовательном соединении нелинейных резисторов в качестве общего аргумента принимается ток, протекающий через последовательно соединенные элементы. Расчет проводится в следующей последовательности. По заданным ВАХ 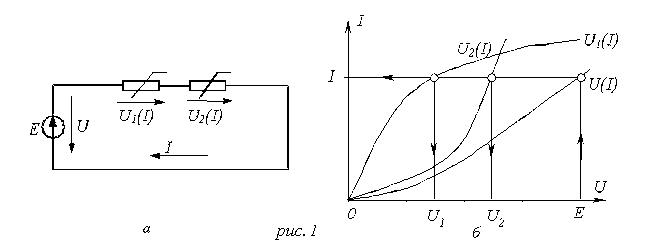 отдельных рез исторов в системе декартовых координат  строится результирующая зависимость . Затем на оси напряжений откладывается точка, соответствующая в выбранном масштабе заданной величине напряжения на входе цепи, из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой  опускается ортогональ на ось токов – полученная точка соответствует искомому току в цепи, по найденному значению которого с использованием зависимостей  определяются напряжения  на отдельных резистивных элементах.

Применение указанной методики иллюстрируют графические построения на рис. 1,б, соответствующие цепи на рис. 1,а.
2) Параллельное соединение

П 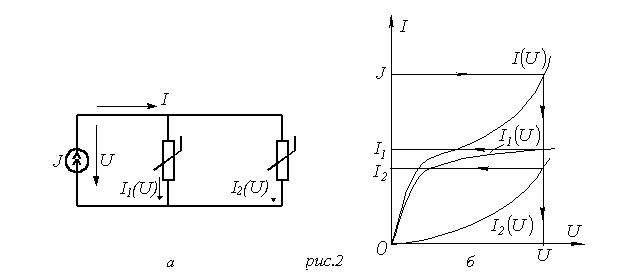ри параллельном соединении нелинейных резисторов в качестве общего аргумента принимается напряжение, приложенное к параллельно соединенным элементам. Расчет проводится в следующей последовательности. По заданным ВАХ  отдельных резисторов в системе декартовых координат  строится результирующая зависимость . Затем на оси токов откладывается точка, соответствующая в выбранном масштабе заданной величине тока источника на входе цепи (при наличии на входе цепи источника напряжения задача решается сразу путем восстановления перпендикуляра из точки, соответствующей заданному напряжению источника, до пересечения с ВАХ ), из которой восстанавливается перпендикуляр до пересечения с зависимостью . Из точки пересечения перпендикуляра с кривой  опускается ортогональ на ось напряжений – полученная точка соответствует напряжению на нелинейных резисторах, по найденному значению которого с использованием зависимостей  определяются токи  в ветвях с отдельными резистивными элементами.

Использование данной методики иллюстрируют графические построения на рис. 2,б, соответствующие цепи на рис. 2,а.

Аппроксимация характеристик нелинейных элементов

Для того чтобы была возможность аналитически рассчитывать цепи с нелинейными элементами, необходимо иметь математические выражения для характеристик элементов. Сами эти характеристики обычно являются экспериментальными, т.е. полученными в результате измерений соответствующих элементов, а затем приводятся как справочные (типовые) данные. Процедуру математического описания некоторой заданной функции в математике называют аппроксимацией этой функции. Существует целый ряд типов аппроксимации: по выбранным точкам, по Тейлору, по Чебышеву и др. В конечном итоге необходимо получить математическое уравнение, которое с какими-то заданными требованиями удовлетворяло исходной, аппроксимирующей функции. Для этого применяют полиномы: степенные, экспоненциальные и тригонометрические.

Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.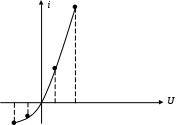







Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точек на заданной функции и составляется система уравнений: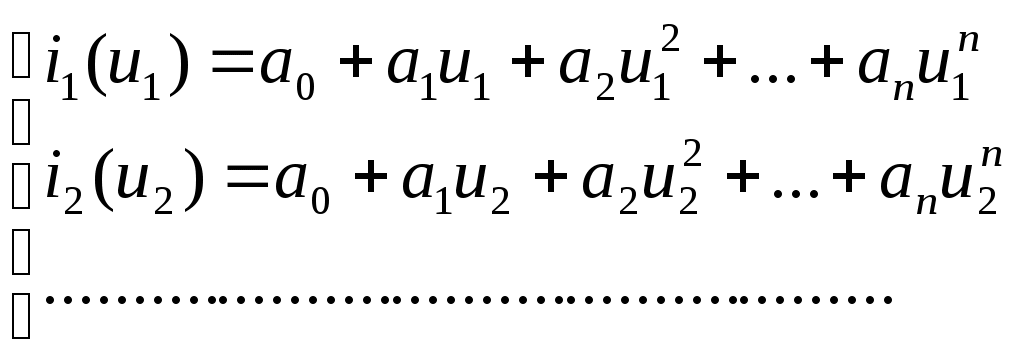



Из этой системы находятся коэффициенты а₀, а₁, а₂, …, а_n.

В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома).

Можно использовать экспоненциальный полином:



Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одно точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные.

Аппроксимация по Батерворту: выбирается простейший полином:

В этом случае можно определить максимальное отклонение ε.



Аппроксимация по Чебышеву является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной.

Ч 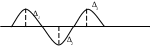ебышев установил, что должно выполняться:




В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий.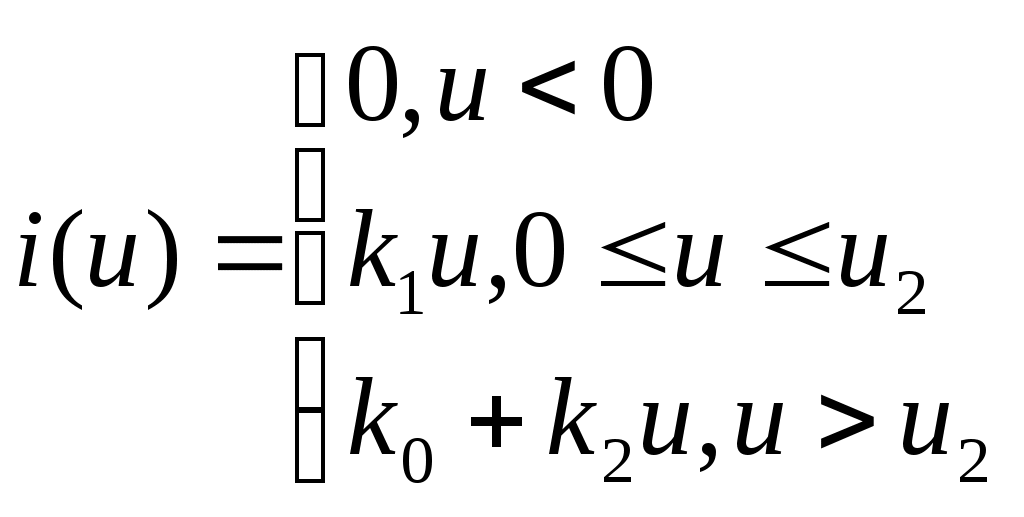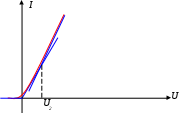