ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
4. Основные принципы и теоремы и методы расчета в теории цепей§1. Метод токов ветвей (МТВ)МТВ основан на непосредственном применении законов Кирхгофа к электрической цепи, приводит к решению системы уравнений. Применяется для сложной цепи, особенно если нельзя определить эквивалентное сопротивление цепи или в цепи действует несколько источников. В качестве основных неизвестных в МТВ используют токи ветвей. В качестве дополнительных неизвестных рассматривают напряжения на идеальных источниках тока. Начинают с определения структурных параметров (количество узлов, независимых контуров, ветвей). По первому закону Кирхгофа составляется (N-1) уравнений, где N – число узлов. По второму закону составляется столько уравнений, сколько независимых контуров в цепи. Причем эти уравнения целесообразно разделить на основные и дополнительные. Поэтому соответственно контуры разделяют на основные и дополнительные. В основные контуры не должны входить идеальные источники тока. Каждый дополнительный контур должен содержать по одному идеальному источнику тока. Дополнительные уравнения, содержащие напряжения на источниках тока, не включают в систему уравнений, а записывают отдельно. Рассмотрим на примере. 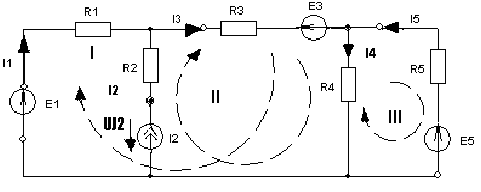 Nуз=3 NуIзк=2 Nосн.ур.=2 Nнк=3 NуIIзк=3 Nдоп.ур.=1. Число неизвестных токов здесь 4 (I1, I3, I4 ,I5) Для составления системы необходимо выбрать направления токов 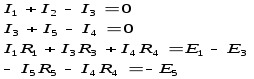 Система уравнений решается и находятся неизвестные токи. Доп. уравнение: §2. Принцип и метод наложения в теории цепей.Принцип наложения или суперпозиции – это физический принцип, который говорит, что результирующее действие, возникающее от действия нескольких сил, может быть в линейной системе найдено как алгебраическая сумма от действий каждой силы в отдельности. В теории цепей под силой рассматривается действие каждого источника. Тогда можно заключить, что ток, который возникает на участке цепи под действием нескольких источников, работающих одновременно, можно определить как алгебраическую сумму частичных токов, каждый из которых возникает под действием своего источника, работающего отдельно от остальных источников. Частичные токи рассчитываются каждый в своей схеме замещения, в которой оставляют один источник, а остальные заменяют следующим образом: идеальный источник тока – разрывом (I=0), идеальный источник напряжения (ЕДС) – перемычкой, проводником (E=0), реальные источники энергии – внутренними сопротивлениями. К полученным схемам применяют законы Кирхгофа, законы Ома. На основе этих положений возникает метод наложения для расчетов токов и напряжений. Особенно он необходим, когда в цепи действует несколько разнотипных источников (например, с разными частотами, с разными видами действия, с разной формой воздействия). Рассмотрим на примере. Пример 1 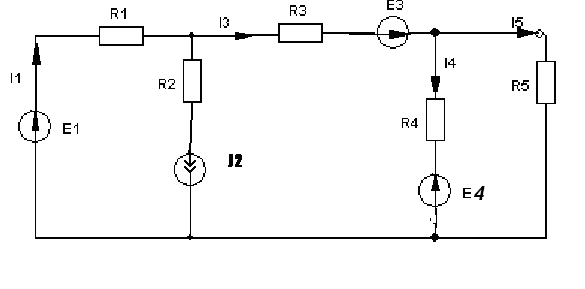 К данной схеме можно применить как метод наложения, так и метод токов ветвей. Составим четыре схемы замещения, в каждой из которых будет действовать только один источник энергии и есть только частичные токи от этого источника.. 1) 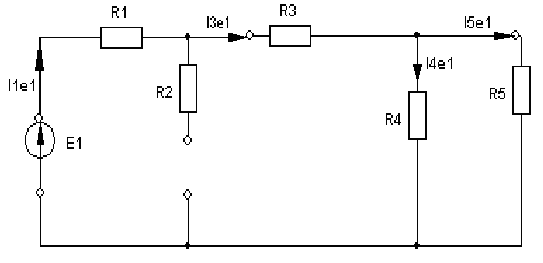 Здесь рассчитывают частичные токи I1Е1 и остальные. 2) 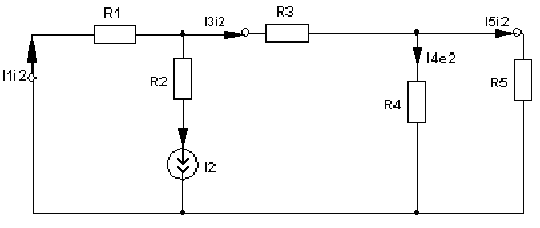 Направления токов не меняем. 3) 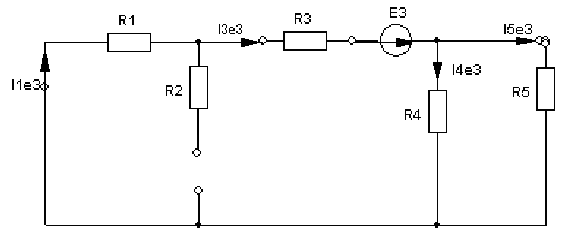 4) 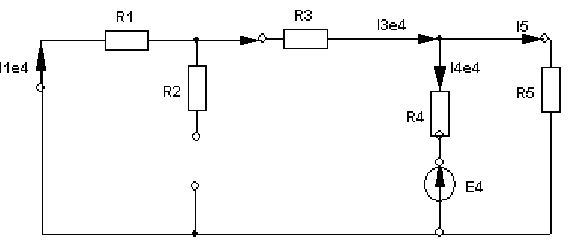 В итоге определяют токи от всех источников , например, I1=I1E1+I1J2+I1E3+I1E4 Как мы видим, в данном примере решение было бы легче при применении метода токов ветвей. Пример 2 Здесь Е1- источник постоянной эдс, а j2 – источник переменного тока 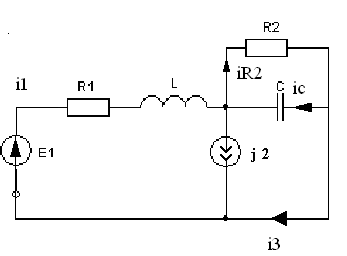 В данном случае мы можем использовать только метод наложения. Составим две схемы замещения, в первой из которых рассчитываются частичные токи от источника постоянной эдс. Поэтому в ней индуктивность заменена перемычкой, а емкость – разрывом. Во второй схеме рассчитываются частичные токи от источника переменного тока и здесь необходимо перевести все токи, напряжения и сопротивления в комплексную форму и записать законы Кирхгофа в комплексной форме. 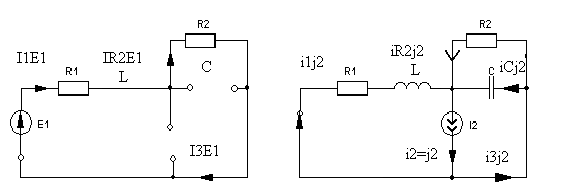 Здесь получается, что i1=I1E1+i1j2, iR2=IR2E1 – iR2j2, ic=icj2, i3=I3E1 – i3j2, i2=j2. §3. Метод контурных токов1. Недостатки МТВ Основной недостаток – довольно большое количество уравнений и соответственно трудоемкость работы. П 2. Основы МКТ В качестве неизвестных здесь используются так называемые контурные токи. Это некоторые условные мысленные токи, протекающие по выбранным независимым контурам. В качестве дополнительных неизвестных берутся напряжения на идеальных источниках тока. Система уравнений составляется только на основе второго закона Кирхгофа с применением закона Ома. Конкретные токи ветвей (действительные токи) определяются как алгебраическая сумма соответствующих контурных токов, протекающих через ветвь. 3. Определение числа уравнений и выбор контуров для МКТ Количество уравнений определяется по формуле: Контуры выбираются так, чтобы в них не входили идеальные источники тока (основные контуры). Дополнительные контуры выбираются с одним источником тока. Их уравнения в систему не включаются, но их влияние учитывается при решении системы. 4. Пример использования 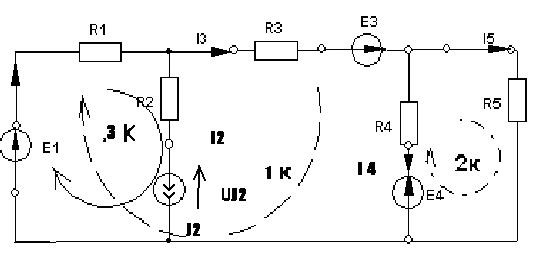 I1 NB=5, NУЗ=3, NИИТ=1. 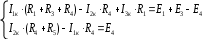 Решив данную систему и определив контурные токи, найдем токи ветвей следующим образом: 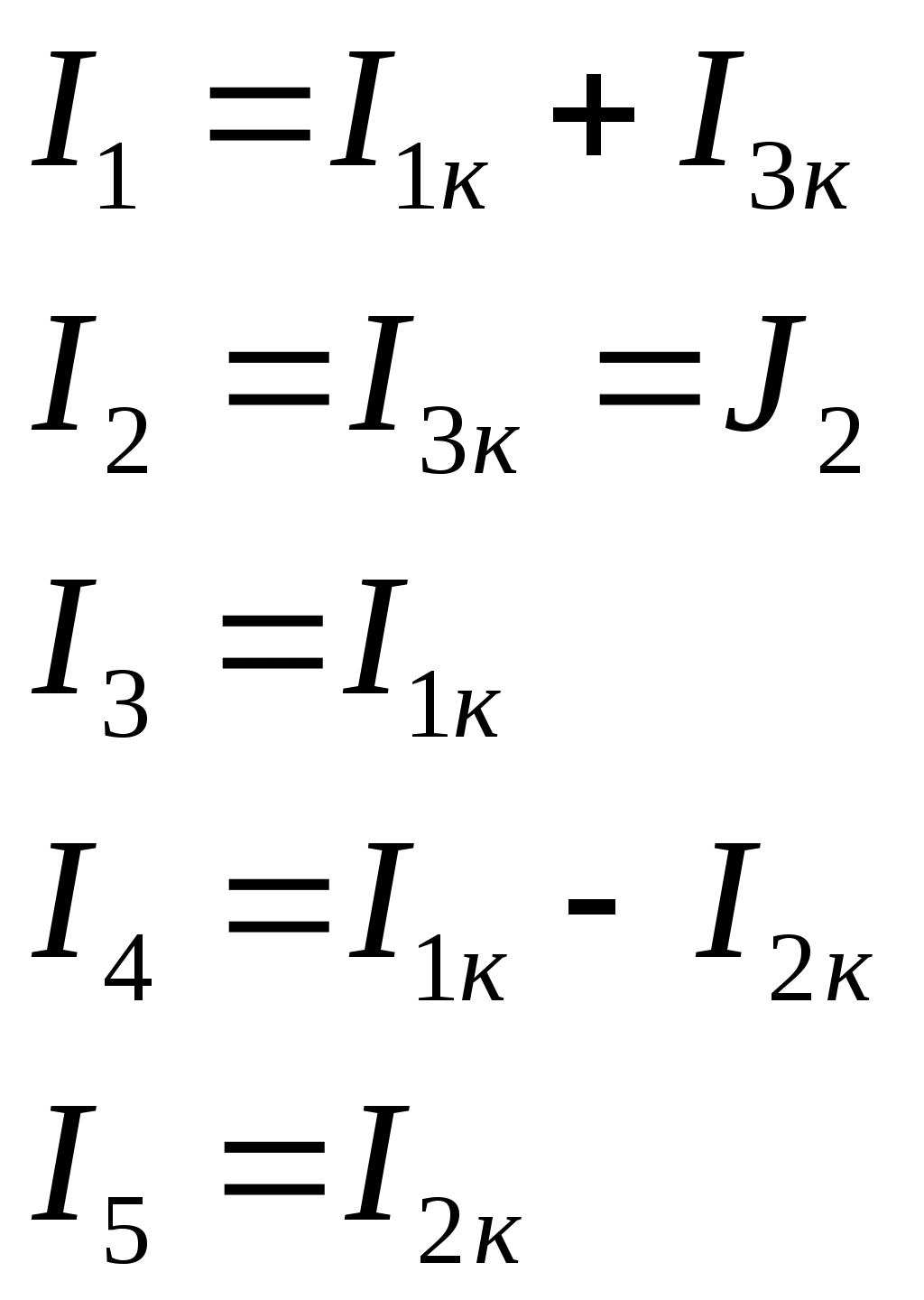  Для определения напряжения на источнике тока составляется вспомогательное уравнение по закону Кирхгофа для дополнительного (3) контура: Можно выделить алгоритм расчета: Определение количества уравнений Выбор основных и дополнительных контуров Составление системы уравнений для контурных токов Решение системы уравнений Определение токов ветвей Определение напряжений на источниках тока 5 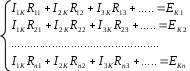 . Общая стандартная форма записи системы уравнений по МКТ . Общая стандартная форма записи системы уравнений по МКТЗаписывают и в матричном виде 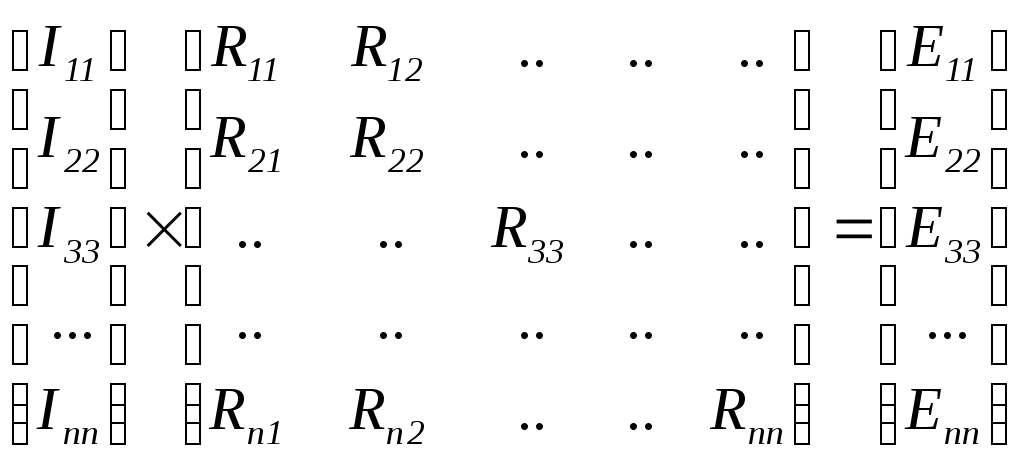 Здесь: IKK – соответствующие контурные токи, R11 – контурное сопротивление первого контура, R22 – второго и т.д.; R12 – взаимное сопротивление между первым и вторым контурами (учитывается с +, если контурные токи совпадают и с - , если не совпадают) и аналогично; E11 – контурная ЭДС 1 контура, которая содержит алгебраическую сумму ЭДС 1 контура и включает влияние источников тока на контур. Далее аналогично. Причем обычноR12 = R21 а если есть управляемые источники, то R12 и R21 могут быть не равны. 6. Применение МКТ Целесообразно применять для сложных схем с несколькими однотипными источниками, у которых частота одна и та же. Если есть L- и C-элементы, то применяется в комплексной форме. Если частоты действия разные, то можно применять совместно с методом наложения для расчета частичных токов. §4. Метод узловых напряжений (МУН)1. Основы МУН В качестве основных неизвестных используются так называемые узловые напряжения – это напряжения между узлом схемы или цепи и некоторым опорным или базисным узлом, который выбирается один для всей цепи или схемы. В качестве дополнительных неизвестных используются токи в некоторых «вырожденных» ветвях, которые содержат только идеальные источники напряжения (или ЭДС) без других элементов. Система уравнений по МУН составляется на основе первого закона Кирхгофа. Второй закон и закон Ома используются как вспомогательные. 2. Определение количества уравнений и выбор базисного узла Количество уравнений определяется по формуле: Базисный узел выбирается из узлов, прилегающих к ветви «вырожденной» (где есть одиночный идеальный источник напряжения). E1  I1 I1 Из этих двух узлов обычно берут тот узел, где больше подходят ветвей. Берут там, где удобнее при взгляде на схему. Начинается метод с определения числа «вырожденных» ветвей и базисного узла, потом составляется и решается система уравнений. 3.Пример применения МУН 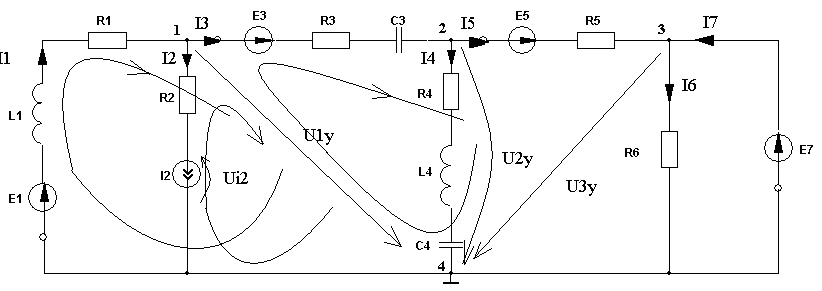 Будем считать, что все источники - гармонического воздействия с одной и той же частотой. Применим метод в комплексной форме. Nуз.=4 NE=1 (Е7) Nур.=4-1-1=2 4 – базисный узел., I2=J2 . Указываем узловые напряжения, направляя их к базисному узлу, при этом 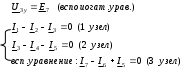 Выразим токи ветвей через узловые напряжения с использованием законов Ома и Кирхгофа. Используем для этого вспомогательные контуры. Выразим токи ветвей через узловые напряжения с использованием законов Ома и Кирхгофа. Используем для этого вспомогательные контуры.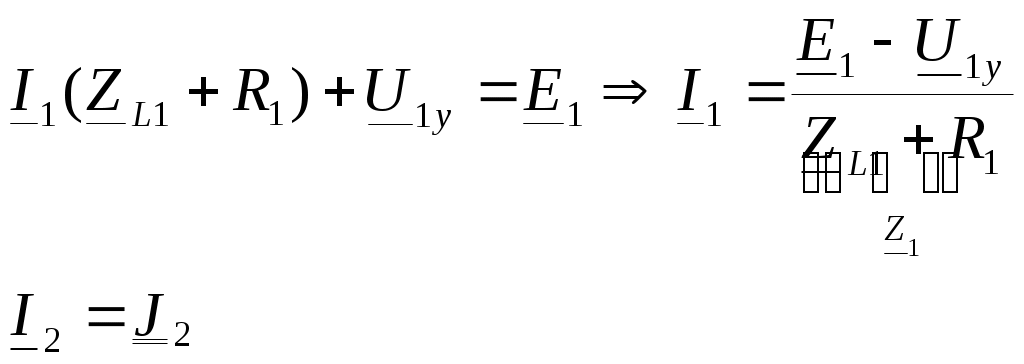 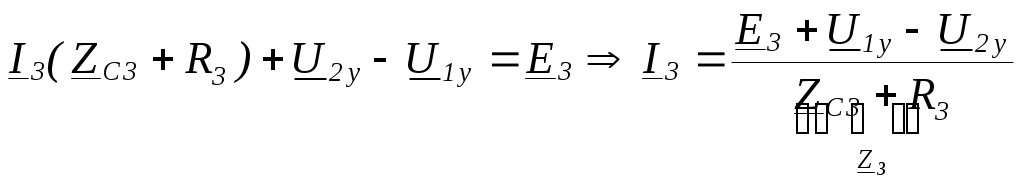 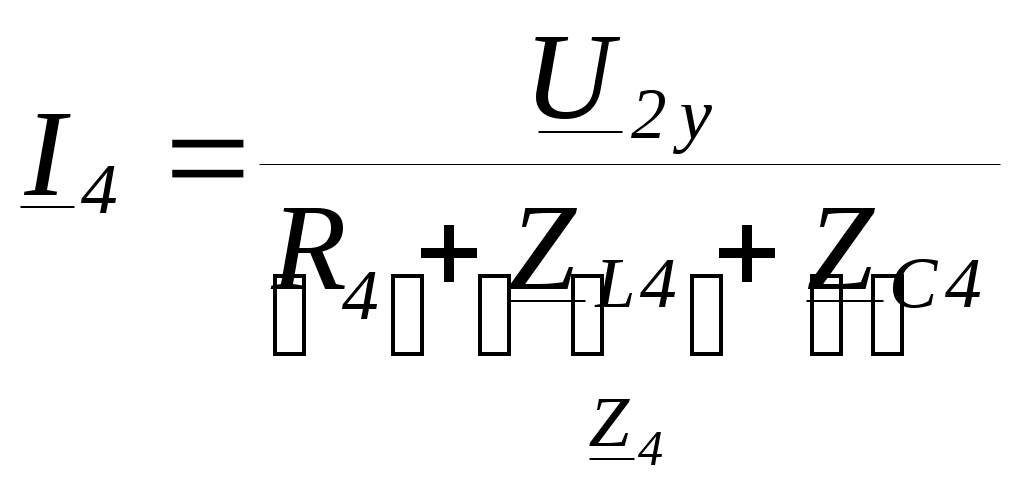 В систему уравнений подставляются формулы токов и делаются алгебраические преобразования, цель которых привести систему к стандартному виду. Стандартный вид: 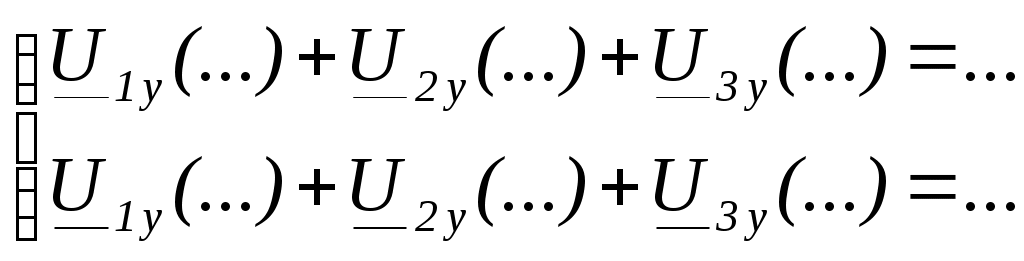 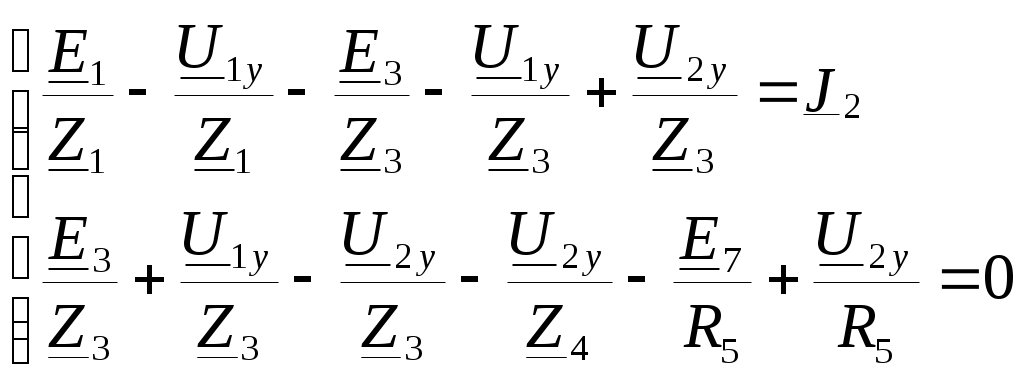 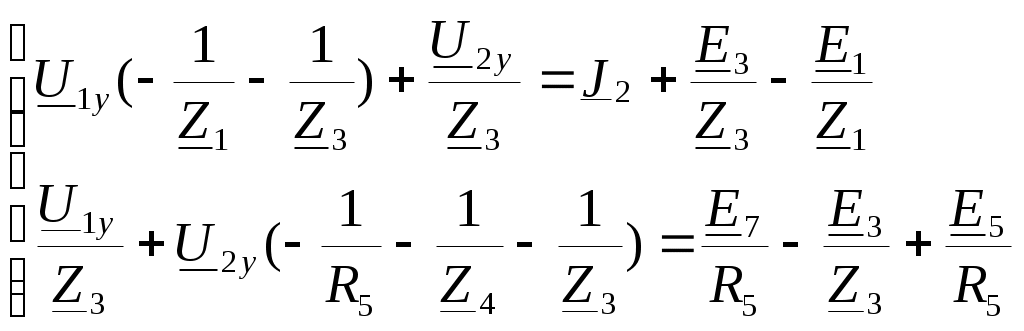 Решив эту систему относительно узловых напряжений, подставляем полученные значения в формулы нахождения токов ветвей через узловые напряжения. Можно сделать смену знаков в уравнениях. 4. Стандартная общая форма записи уравнений по МУН (со сменой знаков) 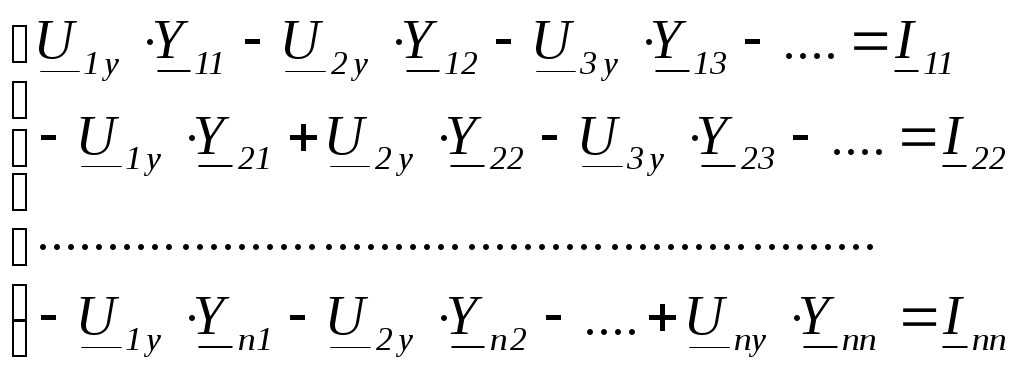 По диагонали знаки с «+», остальные с «-». источник к узлу с«+» от узла – с « - ». например Стандартную систему уравнений можно сразу составлять по схеме, используя понятие проводимостей и токов узлов. На практике используется конечный результат – система уравнений в стандартной форме, она решается потом вычисляются токи ветвей. §5. Принцип дуальности ТЭЦ1. Введение В физике под дуализмом понимают некоторые противоположные, однако, дополняющие и связанные друг с другом понятия, процессы (например, корпускулярно-волновой дуализм). В ОТЦ основные дуальные понятия – это ток и напряжение. Основные дуальные элементы и величины в ТЦ – это индуктивность и емкость, сопротивление и проводимость, узел и контур. В ТЦ есть также дуальные уравнения, по форме похожие, но в них используются дуальные величины. Например, первый и второй законы Кирхгофа. Еще уравнения: Дуальные пары Напряжение ток контур узел индуктивность емкость ИИН ИИТ 1 закон Кирхгофа 2 закон Кирхгофа сопротивление проводимость последовательная цепь параллельная цепь Дуальные уравнения U=I·ZI=U·Y U=U1+U2+U3+U4 I=I1+I2+I3+I4 Z=Z1+Z2+Z3+Z4 Y=Y1+Y2+Y3+Y4 Можно легко переходить от одних уравнений к другим чисто формально, заменяя одни величины в уравнениях на дуальные и все формулы будут правильными, но для дуальных схем . В этом плане метод узловых напряжений дуален методу контурных токов. Там все наоборот. 2. Формулировка принципа дуальности для ЭЦ Если для какой-то цепи справедливо некоторое положение, формула или уравнение, то это будет справедливо для дуальной цепи, если все величины в формуле (уравнении) заменить на дуальные. 3. Составление дуальных схем Этапы: 1) Внутри контуров поставить узлы, и контуры поменять на узлы; 2) Соединить узлы через элементы и все элементы заменить на дуальные. 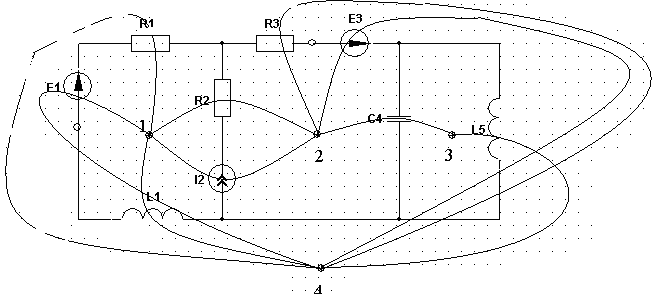 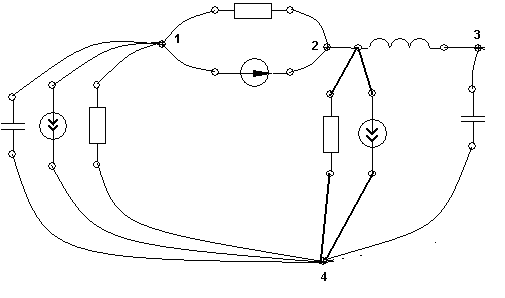 §6. Теоремы об эквивалентных источниках или генераторах(Теорема об автономном двухполюснике)  ЛАЭЦ – линейная активная электрическая цепь, содержит RLC-элементы, источники тока и напряжения. Теорема 1 (об эквивалентном источнике напряжения): Ток в некоторой ветви, подключенной к ЛАЭЦ, не изменится, если эту ЛАЭЦ заменить эквивалентным источником напряжения, содержащим идеальный источник напряжения с ЭДС, равной напряжению холостого хода активной цепи, и эквивалентным сопротивлением, последовательно включенным, равным входному (выходному) сопротивлению пассивизированной активной цепи. 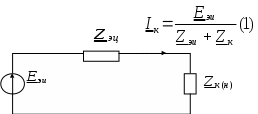 Доказательство: Вставим в выделенную ветвь два одинаковых источника напряжения ЕХ, но противоположных направлений. 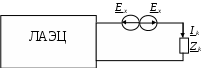 По принципу наложения можно записать:  ), ),  ) и источников внутри ЛАЭЦ. ) и источников внутри ЛАЭЦ.1)в первом случае получим вместо активной цепи пассивизированную цепь (без внутренних источников): 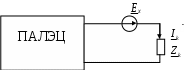 Можем найти 2) Поставим задачу, чтобы 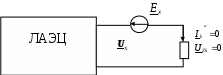 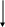 Мы получили не что иное, как режим холостого хода, где UZk=0, и UX=EX=UXX. . Итак, мы доказали, что У нас Теорема 2 (об эквивалентном источнике тока): Ток в некоторой ветви, подключенной к ЛАЭЦ, не изменится, если ЛАЭЦ заменить эквивалентным источником тока, содержащим идеальный источник тока, и параллельно подключенное сопротивление или проводимость; ток идеального источника равен току короткого замыкания ЛАЭЦ; проводимость эквивалентного источника равна входной проводимости пассивизированной ЛАЭЦ. Как видно это дуальная теорема. 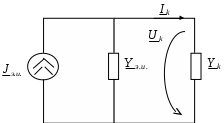 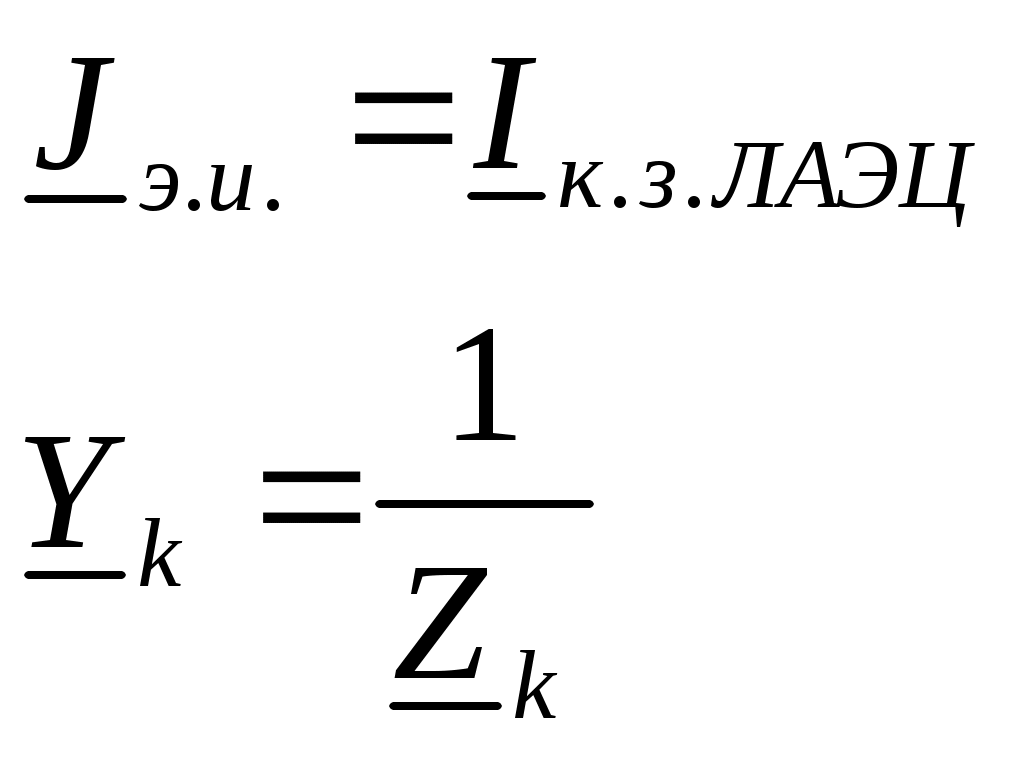 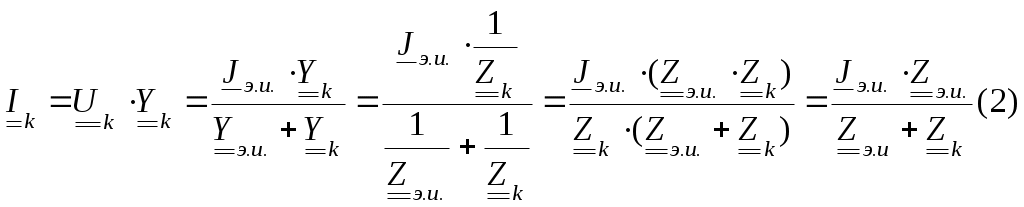 Метод эквивалентного источника напряжения или тока Применяется по соответствующей теореме, когда надо рассчитать один ток в какой-то одной ветви. Для нахождения напряжения холостого хода размыкают ветвь с неизвестным током и находят напряжение Для нахождения Находят §7. Теорема обратимости или взаимностиСправедлива для линейных обратимых цепей: все элементы линейны и обратимы по передаче электрической энергии (движения зарядов) в одну и другую сторону. Теорема Если некоторый источник ЭДС вызывает в какой-то ветви пассивной обратимой цепи некоторый ток, то будучи перемещен в эту вторую ветвь, он вызовет в первой ветви, где раньше был, точно такой же ток. Справедлива и дуальная теорема.   Доказательство Применим метод контурных токов, будем выбирать контуры так, чтобы первая ветвь входила только в один первый контур, а вторая – только во второй контур, тогда токи этих ветвей будут равны этим контурным токам. В первой схеме: 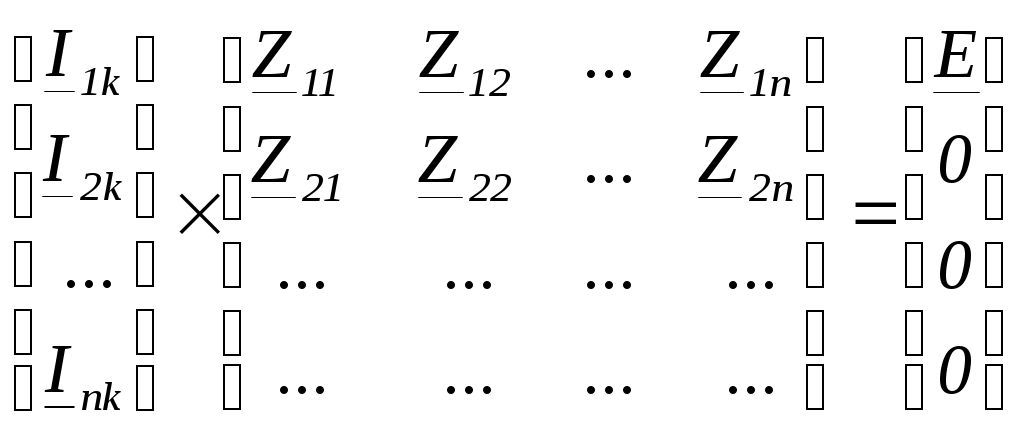 Во второй : 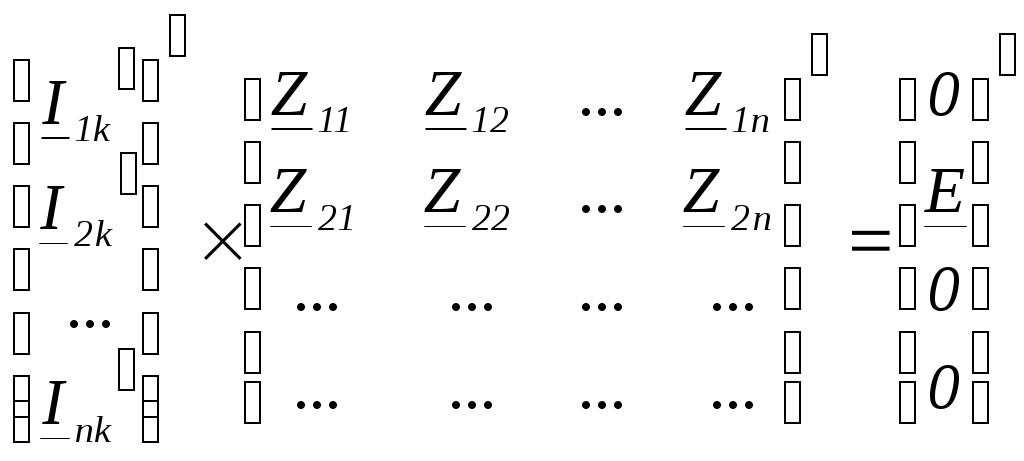 , тогда , тогдаЭти два выражения отличаются на Применение теоремы Теорему целесообразно применять при расчете токов методом наложения, когда надо находить частичные токи от каждого источника в отдельности, рассчитав ток от одного источника напряжения и пропорционально изменяя токи от источников в других ветвях. Примеры Применим МЭИН для нахождения тока I5 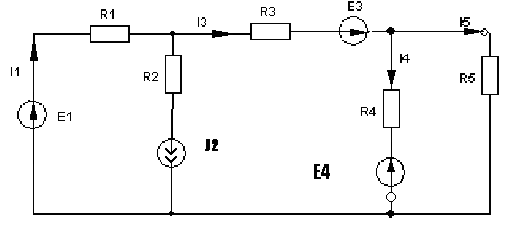 . Рассмотрим схему для нахождения Uxx 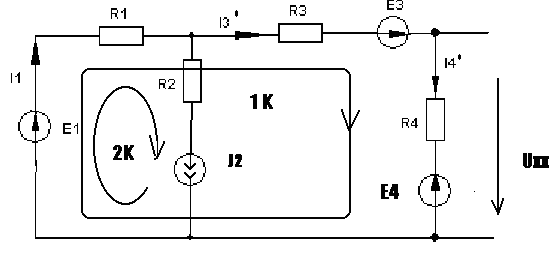 На основе 2 закона Кирхгофа Uxx=I4׳▪R4+E4. Чтобы найти ток I4׳ можно применить МКТ. Тогда получим, что I4׳=I1к и I1к(R1+R3+R4)+J2R1=E1+E3-Е4 Для нахождения Rвх рассмотрим пассивизированную схему (без источников) Rвх 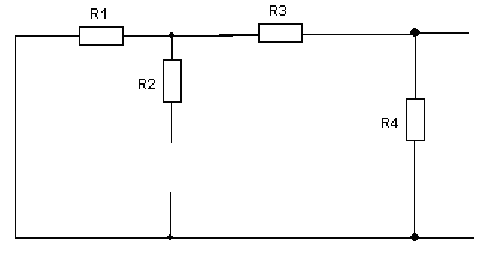 Теорему взаимности целесообразно применять в методе наложения, когда ищутся частичные токи от отдельных источников. Найдя ток от одной ЕДС во всех ветвях можно сразу сказать, что другие ЕДС вызовут в этой ветви токи пропорциональные их отношению. 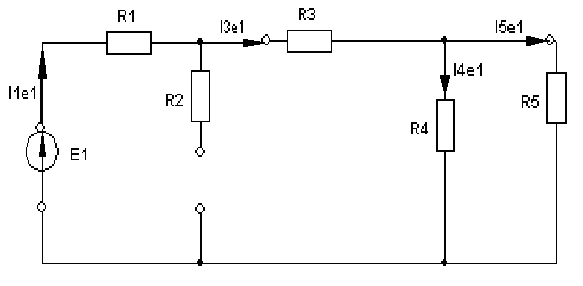 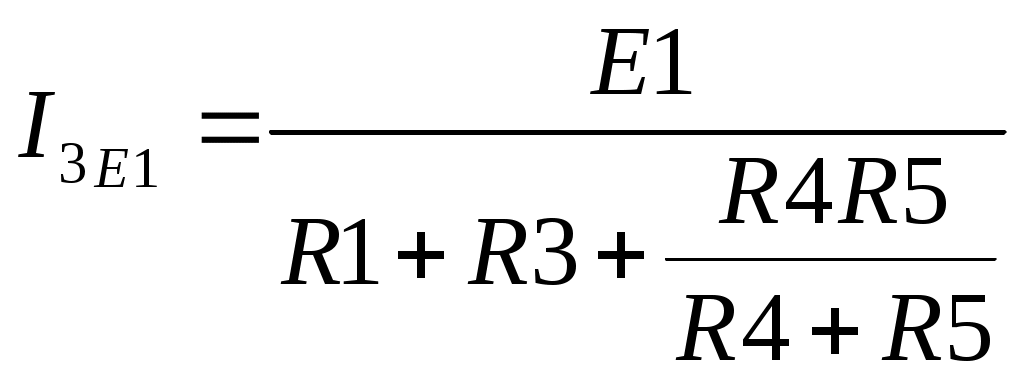 , тогда , тогда 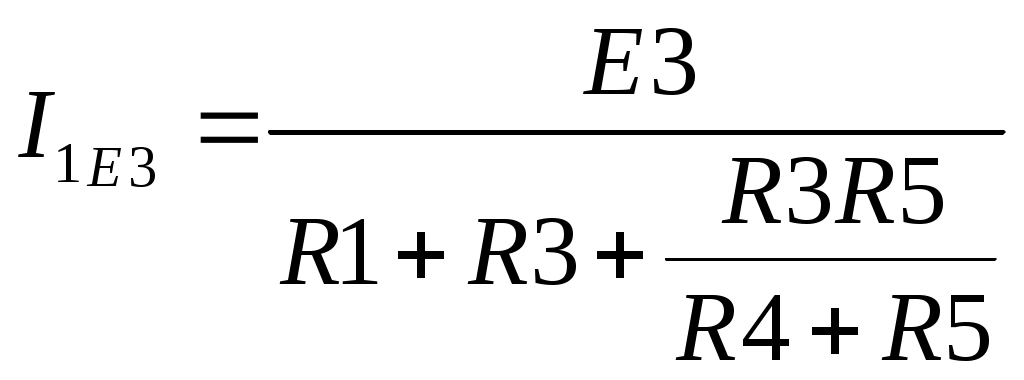 Расчет электрических цепей с управляемыми источникамиРассмотрим схему с транзистором. З 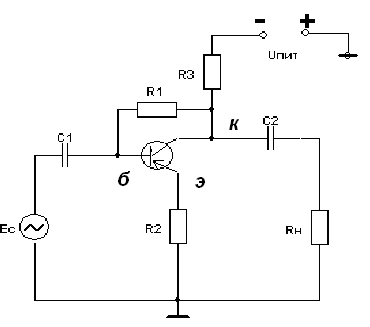 десь есть разные источники eC ( источник сигнала - переменный) и UПИТ( источник питания - постоянный), поэтому применяется метод наложения. Рассмотрим расчет для переменных составляющих, получающихся от действия eC (t). Для этой схемы можно применять любые методы расчета по составленной расчетной эквивалентной схеме, где транзистор заменен схемой замещения с управляемым источником ИТУТ с выражением IK=βIб. . На первом этапе управляемый источник считается независимым и составляется система уравнений по какому-то методу (для гармонического воздействия в комплексной форме). 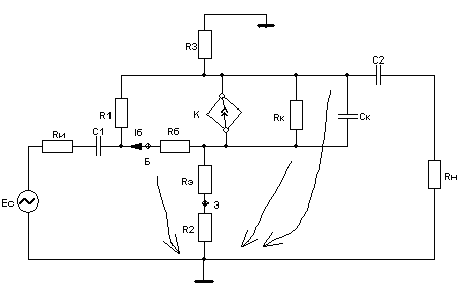 3 узел 1 узел 2 узел U3УЗ U1УЗ U2УЗ 4 узел (базисный) 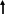  U1УЗ(1/(RИ+ZC1)+1/RБ+1/R1) – U2УЗ1/RБ – U3УЗ1/R1 = EC/ (RИ+ZC1) - U1УЗ (1/RБ) + U2УЗ(1/RБ+1/(RЭ+R2) +1/RK+1/ZCK) – U3УЗ(1/RK+1/ZCK) = - IK - U1УЗ (1/R1) - U2УЗ(1/RK+1/ZCK) + U3УЗ(1/R1+1/R3+1/RK+1/ZCK+1/(ZC2+RH) = = IK На втором этапе вместо тока управляемого источника IК подставляем его значение. На третьем этапе управляющую величину Iб записываем в зависимости от метода для МКТ через контурные токи, а для МУН через узловые напряжения I б =(U2УЗ – U1УЗ) / RБ. Далее делаются алгебраические преобразования и решается система уравнений. Токи определяются по соответствующим формулам, например ток нагрузки IH = U3УЗ/(ZC2+RH) , если направление тока взять вниз.  Усилитель с коэффициентом усиления k. в общем случае, это ИНУН и у простого усилителя k– коэффициент управления – простое число. 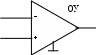 Операционный усилитель, микросхема, и его простейшая схема замещения 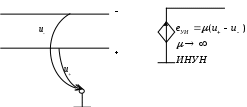 μ – коэффициент усиления операционного усилителя 7. Мощность в цепи переменного тока1. Общие понятия о мощности Мощность – это количество потребленной энергии в единицу времени. В ОТЦ рассматриваются следующие виды мощности: мгновенная – мощность, вычисляемая через мгновенные токи и напряжения; активная – мощность в резистивных элементах; реактивная – мощность в реактивных элементах (L и C); полная – совместная мощность в RLC-элементах; комплексная – мощность, вычисляемая через комплексные токи и напряжения. 2. Мощность в резистивном элементе 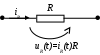 Зададимся гармоническим током Зададимся гармоническим током  - амплитуда мгновенной мощности в R - амплитуда мгновенной мощности в R 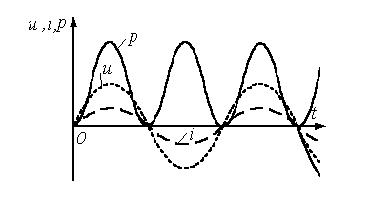 Этим элементом всегда потребляется энергия. Для оценки потребления изменяющееся мощности используется среднее значение мощности за период. Ему дали название активная мощность (P). 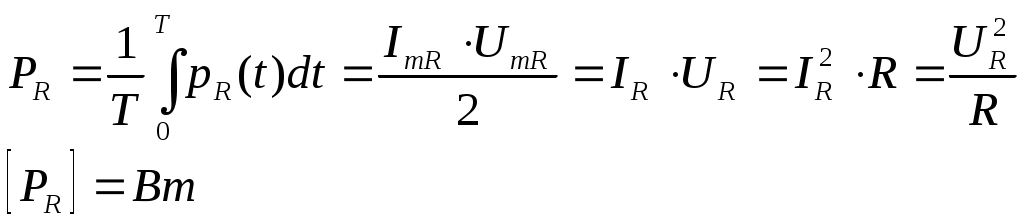 3. Мощность в индуктивном и емкостном элементах (реактивных элементах)  Рассмотрим гармонический ток Рассмотрим гармонический ток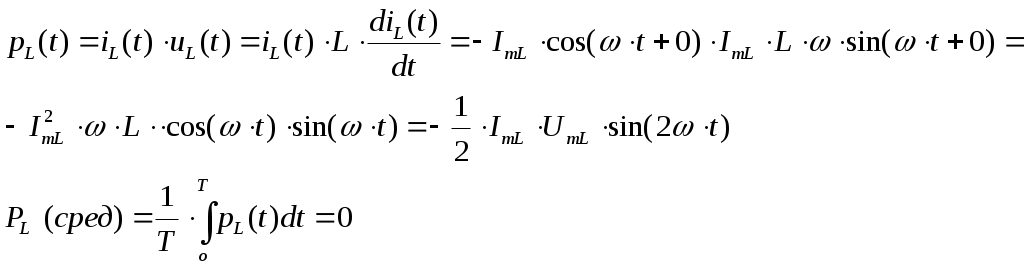 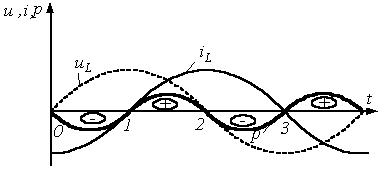 Когда pL(t)> 0. индуктивность запасает энергию, а когда < 0, то возвращает, поэтому ее можно назвать обменной мощностью . Мощность в индуктивности характеризуют амплитудой мгновенной (обменной) мощности: Аналогично в емкостном элементе. Емкостной элемент какое-то время потребляет энергию, какое-то время отдает. (Все это справедливо для идеальных элементов). Здесь рассматривается емкостная мощность QC, которая по смыслу является амплитудой мгновенной (обменной) мощности в емкостном элементе. С учетом того, что мгновенная емкостная мощность противоположна по фазе индуктивной, то Можно определять и общую реактивную мощность: Q=QL+ QC Если есть разнотипные элементы, то еще определяется полная мощность S (аналогично полному сопротивлению), поскольку мгновенная реактивная мощность по фазе колебания сдвинута относительно мгновенной активной на четверть периода (900), то: 4. Мощность на участке электрической цепи  Для цепи при гармоническом воздействии можно записать Для цепи при гармоническом воздействии можно записать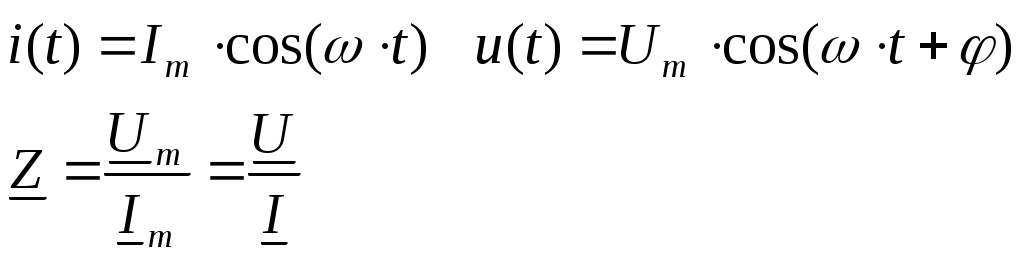 Можно определить мгновенную мощность на участке цепи p(t)=u(t)i(t) Если использовать свойства тригонометрических функций, то мгновенную мощность можно расписать на мгновенную активную мощность и мгновенную реактивную мощность и выделить постоянную составляющую - среднее значение (активную мощность). 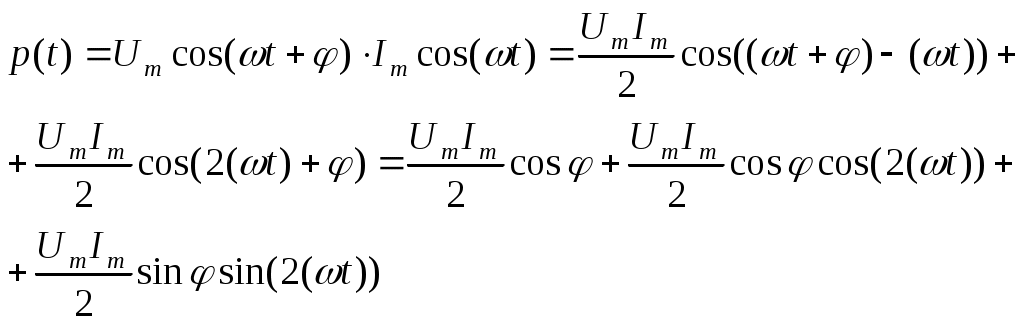 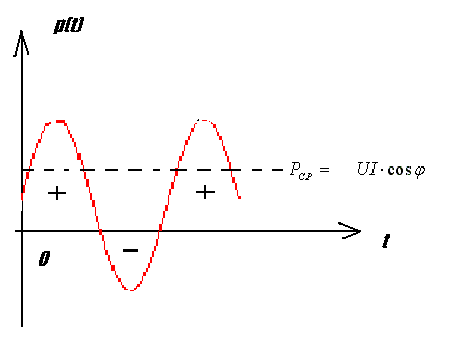 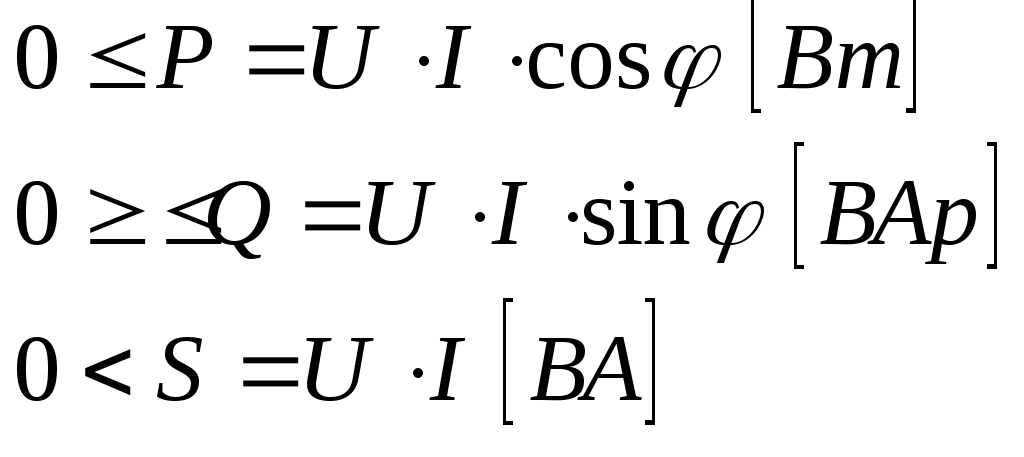 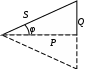 Треугольник мощностей: Полная мощность – максимально возможная активная мощность (cosφ =1). 5. Комплексная мощность Поскольку при расчетах с гармоническими токами используются комплексные токи и напряжения, то целесообразно ввести понятие комплексной мощности. где символ * - переход к комплексно сопряженному числу. Рассмотрим мощности источников:  pe(t)= i(t)e(t)=pa(t)+pp(t) Это меняющаяся величина. pe(t)= i(t)e(t)=pa(t)+pp(t) Это меняющаяся величина.(если ток противоположен ЕДС, то в формуле мощности берется знак - ) Д  ля комплексной формы ля комплексной формы (если ток взят противоположного направления ЭДС, то следует поставить знак - ). Здесь так же выделяют активную (среднюю за период) и реактивную (амплитуду обмена ) мощности источника. Аналогично для источника тока  pJ(t)=j(t)uJ(t) . Если напряжение источника выбрать не противоположно току то надо в формуле мощности ставить знак - . В комплексной форме  Активная мощность определяет энергию, которую в среднем отдает источник за период, а реактивная определяет .амплитуду обменной мощности источника, которой он обменивается с пассивными элементами цепи при гармоническом воздействии... 6. Баланс мощностей Под балансом понимают равенство: мощность, отдаваемая источниками энергии, должна равняться мощности, потребляемой нагрузками электрической цепи. Это довольно легко определяется на постоянном токе. На переменном токе баланс должен соблюдаться отдельно по активным и реактивным мощностям или в комплексной форме. С какой скоростью источник отдает энергию, с такой скоростью ее получает нагрузка. Математически в общем виде баланс можно записать: Для участка цепи из RLC-элементов 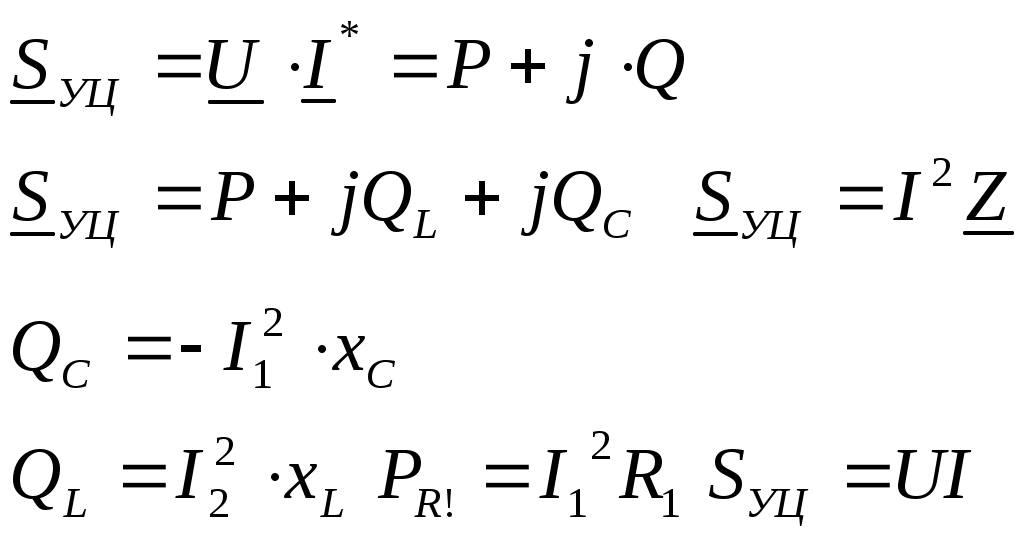  P=PR. Q=OL+QC Рассмотрим баланс для более сложной схемы, но где источники имеют одну и ту же частоту. К 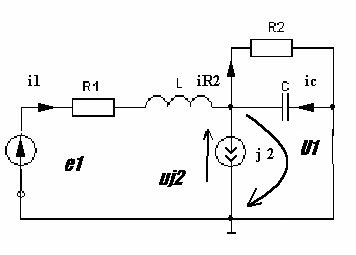 омплексная мощность источников будет равна омплексная мощность источников будет равна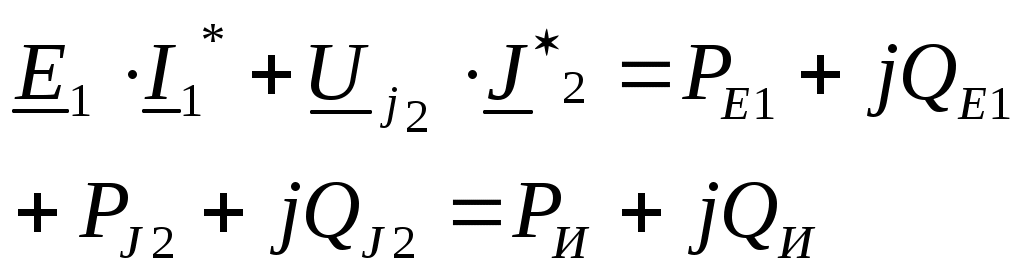 Мощность нагрузок 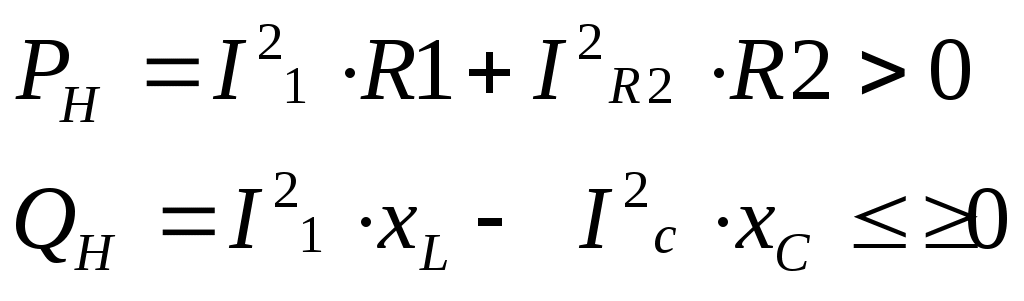 PИ>0., но РE1 и PJ2 ?.Один из источников может и потреблять энергию (находится в режиме зарядки - аккумулятор). Тогда для него активная мощность отрицательна. Для тренировки запишем для этой схемы уравнения по МУН. Здесь два узла и всего 1 уравнение. 7. Условия передачи максимума активной мощности источника в нагрузку Рассмотрим источник электрической энергии (ИЭЭ), подключенный к нагрузке (потребителю энергии).. Для расчета применяются схемы замещения: 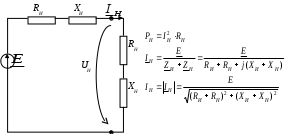 IН – max при min знаменателя. 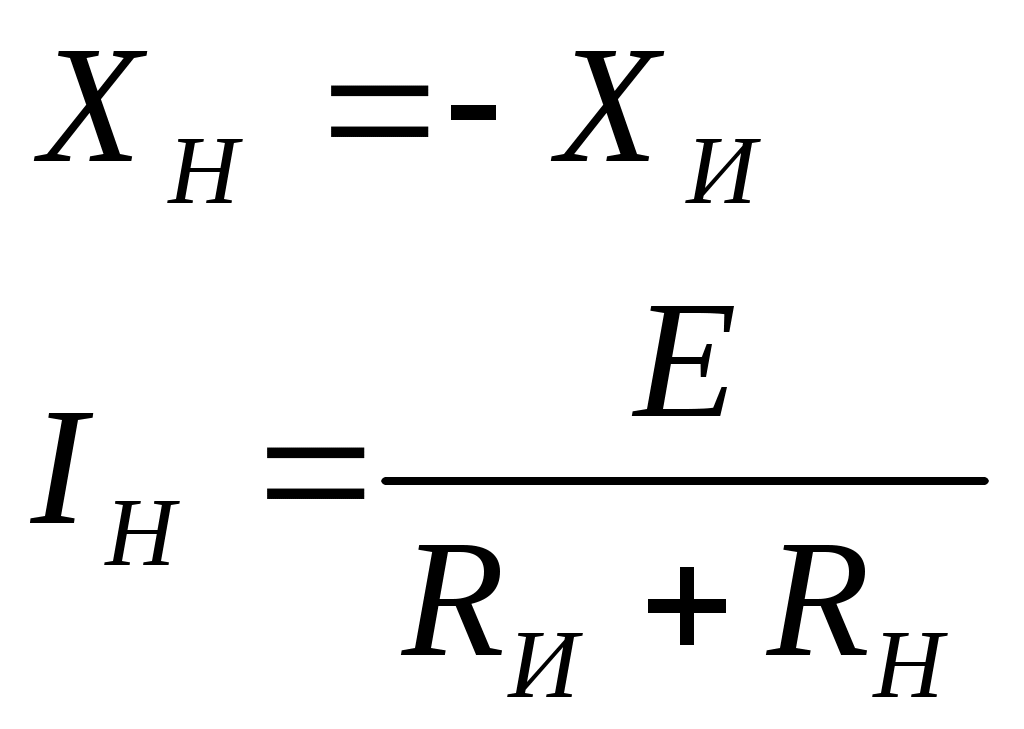 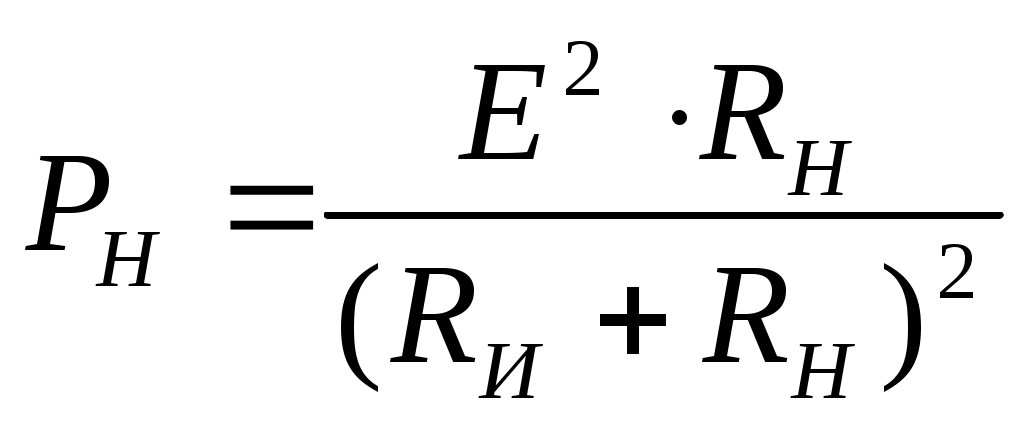 Но при каком сопротивлении нагрузки PН будет максимальна? Найдем производную по RH. 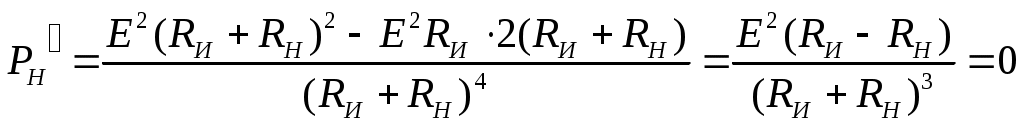 Дпя этого 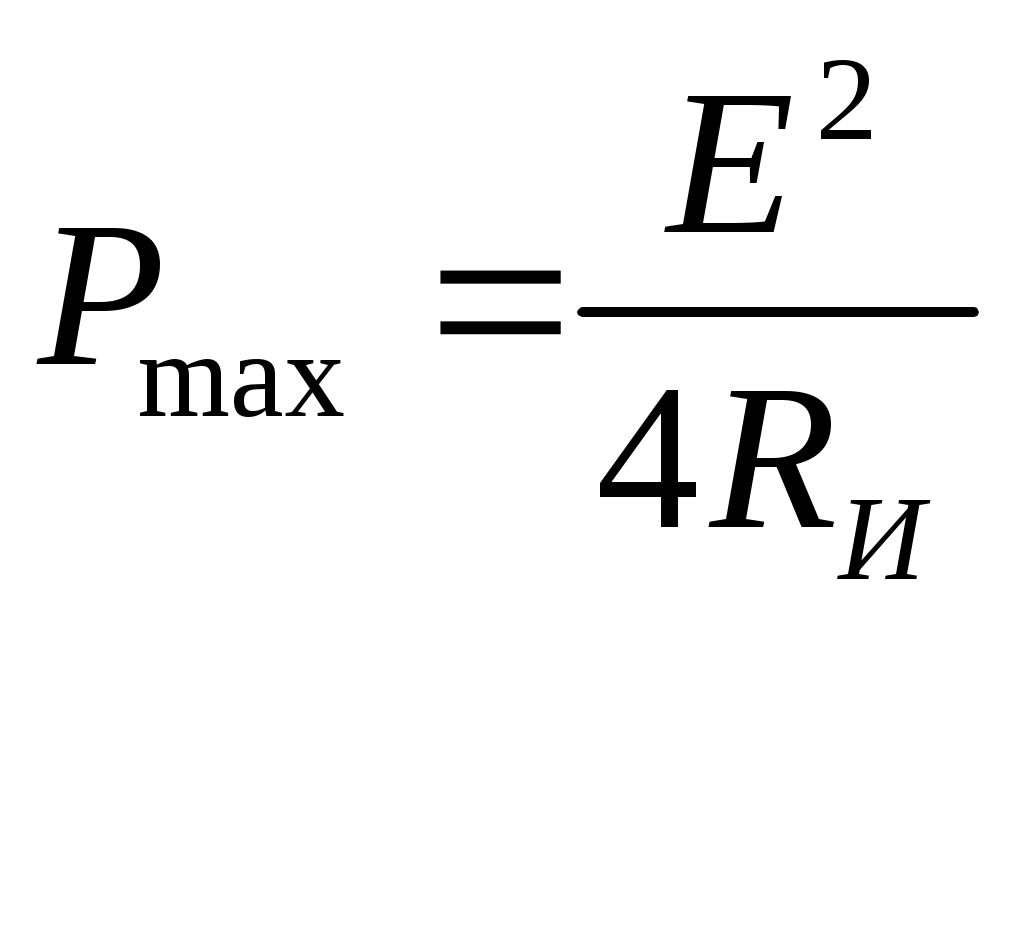 при этом кпд при этом кпд Так как Q=UIsinφ, то они требуют чтобыφ=0 и у потребителей cosφ=1. Потребляемая мощность P=UIcosφ. И если, например, cosφ=0,5, то ток надо увеличить в 2 раза для получения той же мощности у потребителя (напряжение стандартно и не меняется). Тогда потери в соединительных проводниках возрастут в 4 раза. Это не экономично. Для уменьшения потерь энергии при передачи электричества повышают напряжение в линиях передачи, чтобы уменьшить ток (высоковольтные ЛЭП). Большинство нагрузок носят по сопротивлению индуктивный характер (обмотки электромоторов), поэтому потребители у себя включают параллельно на входе своей цепи специальные батареи компенсирующих конденсаторов. Суммарная величина емкости такой батареи подбирается примерно равной общей индуктивной нагрузке. В системах передачи информации применяются маломощные сигналы и можно допустить КПД 0,5 и получить максимум мощности, но более важно сохранить неизменность информации (или неискаженность сигнала). Для этого используется условие Параллельные RLC - цепиРассмотрим схему с параллельными RLC - элементами: 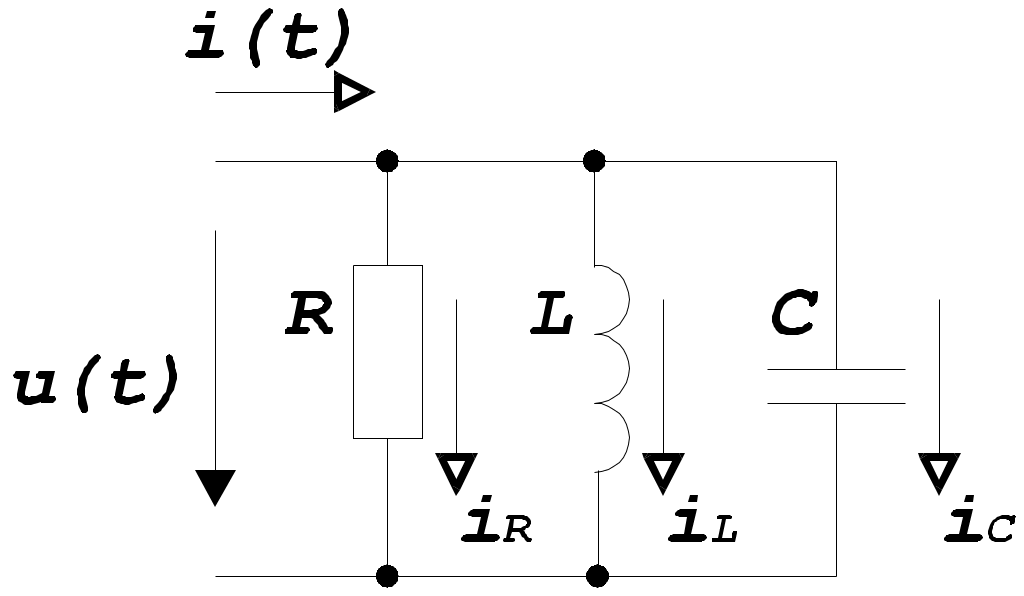 Все ее элементы соединены параллельно и находятся под одним и тем же напряжением u(t)=Umsin(t+u). Необходимо определить ток в цепи i(t). На основании 1-го закона Кирхгофа в любой момент времени справедливо соотношение i(t)=iR(t)+iL(t)+iC(t) . Отдельные составляющие токов определяются выражениями Подставив вместо u(t) гармоническую функцию времени и проведя необходимые математические операции, получим Будем определять искомый ток в виде i(t)=Imsin(t+i). Перейдем к комплексным мгновенным значениям. Сокращая на ejt и учтя, что или Выражение в скобках – комплексная проводимость цепи Y на какой-то частоте ω0, которую называют резонансной. Закон Ома в комплексной форме для цепи записывается Отсюда следует, что при параллельном соединении ветвей цепи комплексная эквивалентная проводимость равна сумме комплексных проводимостей ветвей: 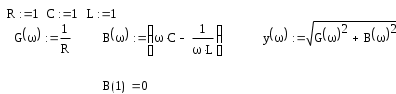 ω0=1 ω0=1 Посмотрим графики зависимостей проводимостей от частоты 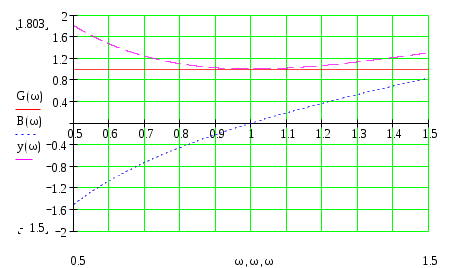 Проанализируем векторную диаграмму параллельной RLC - цепи 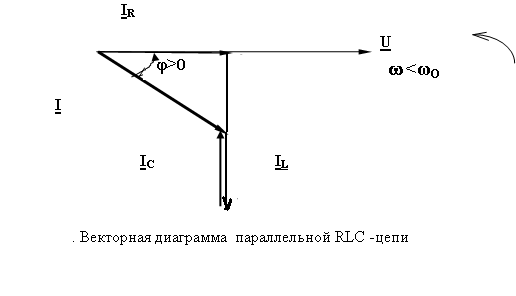 Напряжение взято как опорный вектор, ток в резисторе совпадает по фазе с напряжением , ток в индуктивности отстает на 900, а ток емкостной опережает на 900 и меньше. Общий ток равен сумме векторов всех токов и он отстает от напряжения по фазе. Для примера можно рассмотреть и временные зависимости напряжения и тока 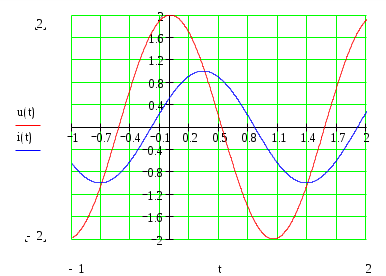 Здесь ΨU=0 , ΨI=-1 рад , φ= 1.. В частных случаях RC или RL – цепей можно использовать общие формулы, убрав соответствующий элемент. 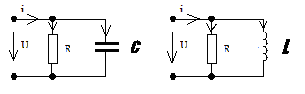 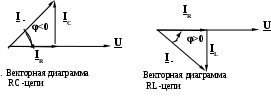 |
