ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
 Скачать 3.24 Mb.
|
3. Анализ режима гармонического тока в линейных электрических цепях3.1. Основные понятия гармонического тока и напряженияПод гармоническим током (напряжением) понимают ток (напряжение), изменяющийся во времени по гармоническому закону cos или sin. Такая функция описывается тремя независимыми параметрами: амплитудой, периодом повторения, начальной фазой. i(t)=Imsin (ωt+ψa)) , ψa>0- начальная фаза, некоторый угол, который получается при t=0; (может быть больше или меньше 0, это зависит от выбора начала отсчета).. В данном случае >0. так как отсчитывается по оси времени от точки, где синус равен 0. ω=2πf (рад/с)– угловая частота, f=1/Tциклическая частота (Гц). 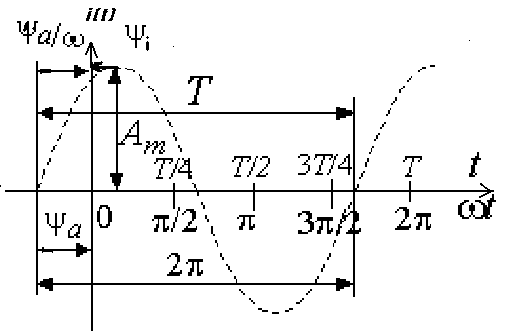 Можно записать ток и через косинус i(t)=Imcos(ωt+ψi) ψi < 0– начальная фаза (в этом случае она отсчитывается против оси времени от точки где косинус равен1) 3.2. Оценка гармонического тока (напряжения)Стандартно меняющуюся величину оценивают по среднему значению, но для функций синуса или косинуса среднее значение равно 0. Можно оценивать по амплитудному значению, но оно кратковременно и поэтому трудно измеримо. Начали оценивать ток (напряжение) по среднеквадратичному значению за период, которое технически называют действующим значением. 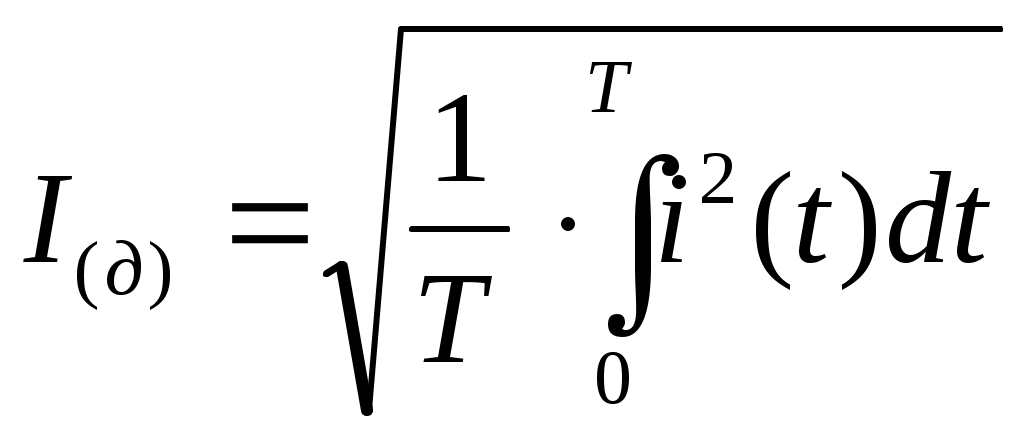 Если мы возьмем гармоническую функцию (синусоиду), то  .Понятие действующего значения используется для оценки и сравнения гармонических токов и напряжений. Практически все приборы, измеряющие переменные токи и напряжения, градуируются в действующих значениях. Физический смысл действующего значения: действующее значение переменного или гармонического тока (напряжения) численно равно такому значению постоянного тока (напряжения), которое действует так же, как и переменный по выделению тепла в таком же сопротивлении за то же время. Рпост = I2▪R, Pпер = Im2▪R/2 =I2▪R. 3.3. Векторное и комплексное представление гармонических функцийПри анализе цепей с переменными токами, напряжениями возникает задача вычисления переменных токов, напряжений, например, их сложения по первому закону Кирхгофа. Как сложить 3-4 синусоиды? 1) Можно графически, но это трудоемко и неудобно. 2) Можно применить векторную математику. 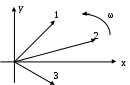 Гармонические функции представляют вращающимися векторами. Через период вектор занимает то же положение. Если частота вращения векторов одинаковая, то результат суммирования величин останется неизменным, будет меняться только угол. Векторные операции более приемлемы для расчетов, но тоже не совсем удобны, поскольку сложно получить точные численные результаты. 3) Можно применить немного другую математику. Например, суммировать векторы по проекциям. По отдельности суммируют вертикальные и горизонтальные проекции. Отсюда один шаг до комплексных чисел, поскольку комплексное число представляет собой вектор с двумя проекциями: вещественной и мнимой частью. Вычисления над гармоническими функциями можно заменить вычислениями над комплексными числами, если у них одна и та же частота колебаний. Поэтому гармонические токи и напряжения символически описываются комплексными амплитудными или действующими значениями. При этом используют действующие или амплитудные значения и начальные фазы колебаний и показательную форму записи комплексного числа.   Для косинусоидальной функции i(t)=Re(ImejΨi▪ejωt)Все можно считать очень точно, применяя математику комплексных чисел.  -множитель вращения  (cos)§4. Законы Кирхгофа в комплексной формеВ общем виде законы Кирхгофа соблюдаются для мгновенных значений, то есть для функций времени. Для простых действующих или амплитудных значений эти законы не соблюдаются. Законы соблюдаются только при учете начальных фаз колебаний, то есть в векторной или комплексной форме как бы при остановке времени. Должна быть одна и та же частота у всех токов или напряжений. Поэтому чисто математически законы Кирхгофа можно записать для комплексных действующих или амплитудных значений при одинаковой частоте колебаний. i 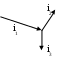 1 - i2 – i3 = 0Im1 – Im2 – Im3 ≠ 0   Аналогично для напряжений. После введения таких символических понятий, как комплексные токи и напряжения, можно ввести понятие комплексного сопротивления для участка цепи.  ;  - модуль комплексного сопротивления (полное сопротивление цепи, характеризует отношение величины напряжения участка цепи к величине тока через этот участок ) - аргумент комплексного сопротивления (характеризует сдвиг фаз между напряжением и током данного участка цепи) , где Rэ – вещественная часть – резистивное сопротивление (активное);Xэ – мнимая часть – реактивное сопротивление. Применяют понятие и комплексной проводимости, как величины, обратной комплексному сопротивлению.  , где y – модуль комплексной проводимости цепи, (полная проводимость).Ψ= - φ. Понятия комплексного сопротивления и проводимости являются основополагающими в первом семестре, так как все основные выводы будут базироваться на использовании этих величин. §5. Анализ режима гармонического тока в пассивных элементахэлектрической цепи 1. Гармонический ток в резисторе 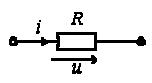  ,  UmR=R▪Im , сдвиг фаз между напряжением и током в резисторе 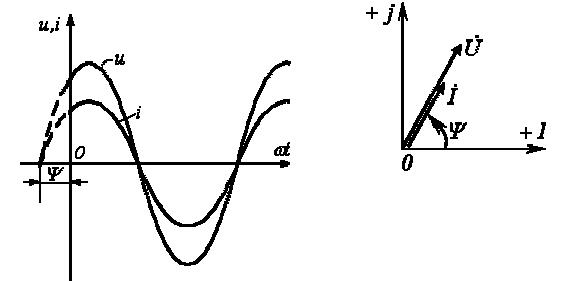 , то есть колебание напряжения совпадает по фазе с колебанием тока,  . 2. Ток в индуктивности 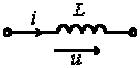 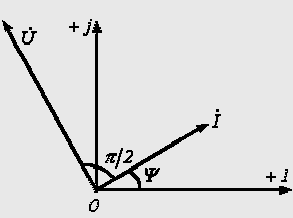 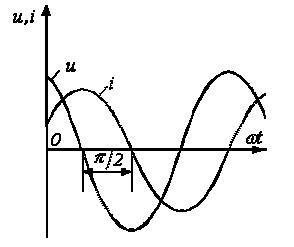  ,  Im=Im▪eΨiUmL=Um▪eΨi+π/2  - индуктивное сопротивление, φL = π/2 > 0 – фазовый сдвиг в индуктивности между колебаниями напряжения и тока, то есть напряжение опережает ток на π/2 (900) или четверть периода.   - Комплексное сопротивление индуктивности.3. Ток в емкости 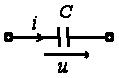 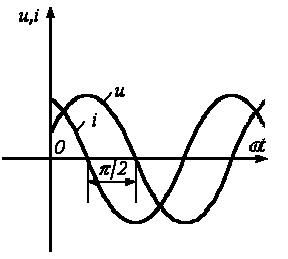 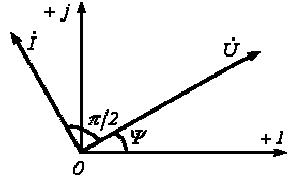  - емкостное сопротивление, φС = - π/2 < 0 – фазовый сдвиг в емкости между колебаниями напряжения и тока, то есть напряжение отстает от тока на π/2 (900) или четверть периода.  Im=Im▪eΨiUmC=UmC▪eΨi-π/2  - комплексное сопротивление емкости.§6. Анализ последовательных R, L, C – цепей при гармоническомвоздействии 1. Анализ RL-цепочки 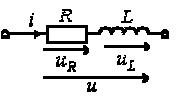 На основе второго закона Кирхгофа  Приведем уравнение в комплексную форму на основе того, что частота тока и напряжения будет одна и та же.  Получим алгебраическое выражение: 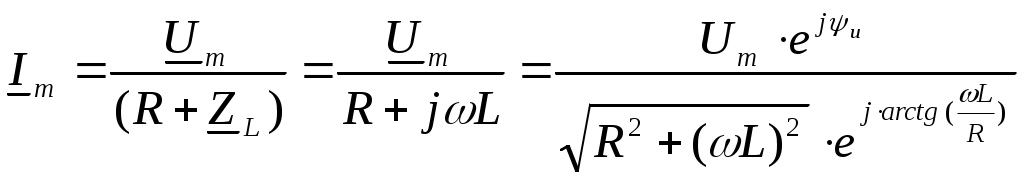 , где  - полное сопротивление RL-цепи; а  - комплексное сопротивление. - сдвиг фаз между напряжением и током в RL-цепи. В RL-цепи напряжение опережает ток на угол меньше чем 900.  Частотные характеристики при Um=const  0 0   0 0  Треугольник сопротивлений и векторная диаграмма 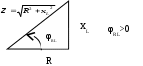 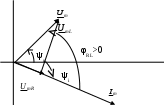   2. Анализ RC-цепочки На основе второго закона Кирхгофа   Переведем в комплексную форму на основе того, что частота тока и напряжения будет одна и та же.  Получим алгебраическое выражение 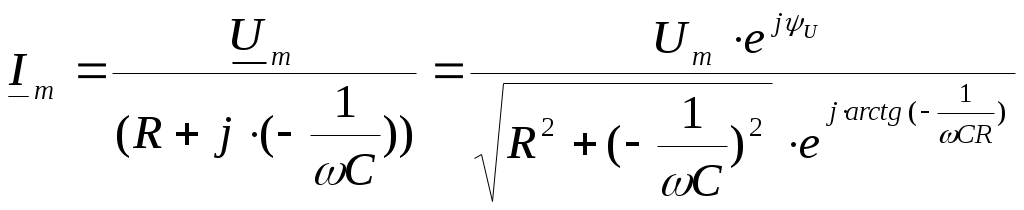 , где  - полное сопротивление RC-цепи; а  - комплексное сопротивление.  - сдвиг фаз между колебаниями напряжения и тока в RC-цепи. В RC-цепи ток опережает напряжение на угол меньше 900.. Частотные характеристики при Um=const 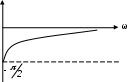 φRC 0 0   0 0  Треугольник сопротивлений и векторная диаграмма 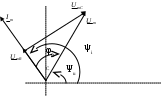 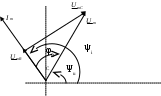 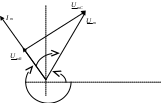 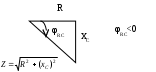   3. Анализ последовательной RLC-цепи при гармоническом воздействии Н 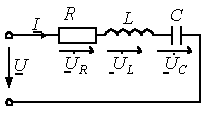 а основе второго закона Кирхгофа u = uR+uL+uC илиU=UR+UL+UC С учетом 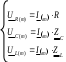 получим где  - комплексное сопротивление последовательной RLC - цепиПреобразовав, получаем, что 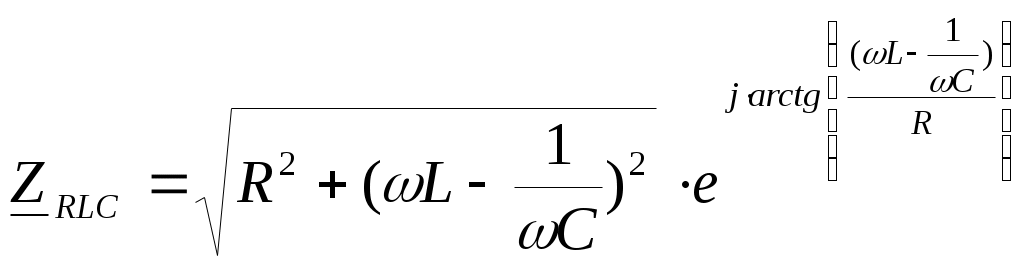 , где  - реактивное сопротивление,  - полное сопротивление цепи, а  - угол сдвига фаз последовательной RLC цепи. Запишем закон Ома в комплексной форме с учетом фазовых соотношений:  . Здесь  .Треугольник сопротивлений в RLC – цепи. 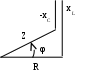 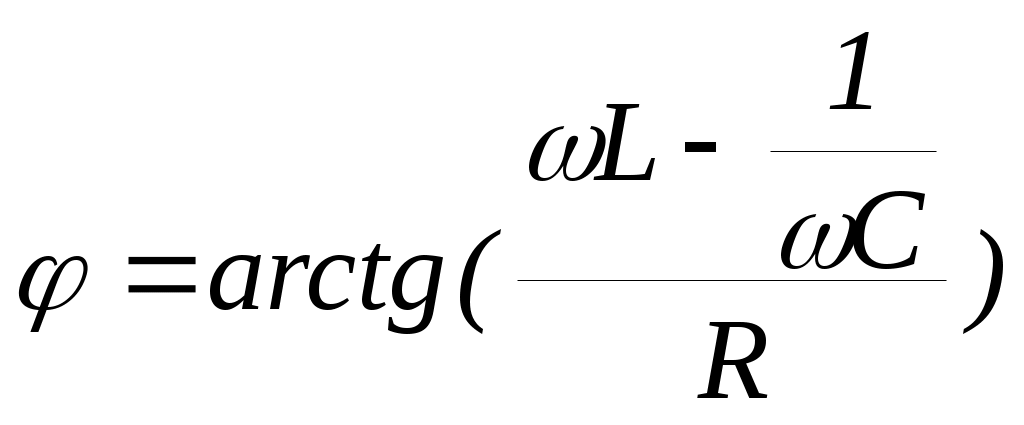 - полное сопротивление RLC - цепи, угол сдвига фаз RLC - цепи. 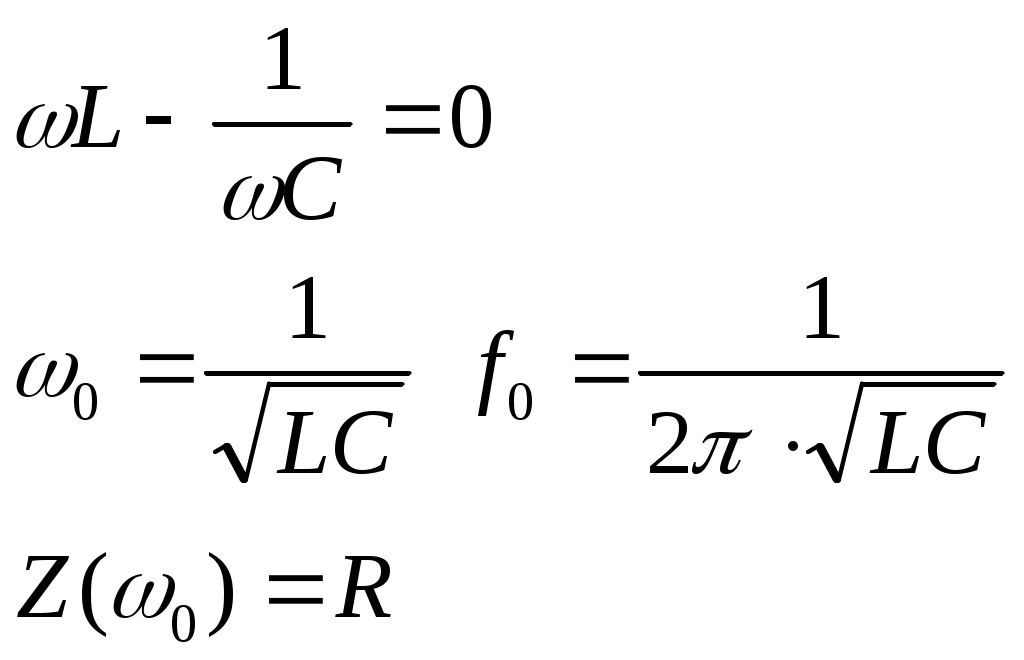 Рассмотрим зависимости Z и угла φ в последовательной RLC-цепи.  0 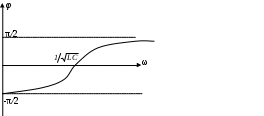 0 φ(0)= - π/2 φ(∞)= π/2 ω0 – резонансная частота RLC– цепи там где сдвиг фаз равен 0. До ω0 напряжение отстает от тока, после ω0 напряжение опережает ток. Графики тока и напряжения на резисторе 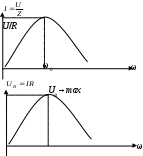 0 0 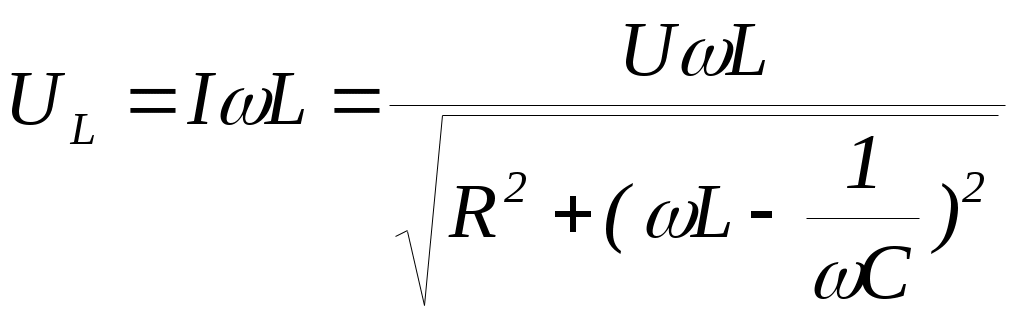 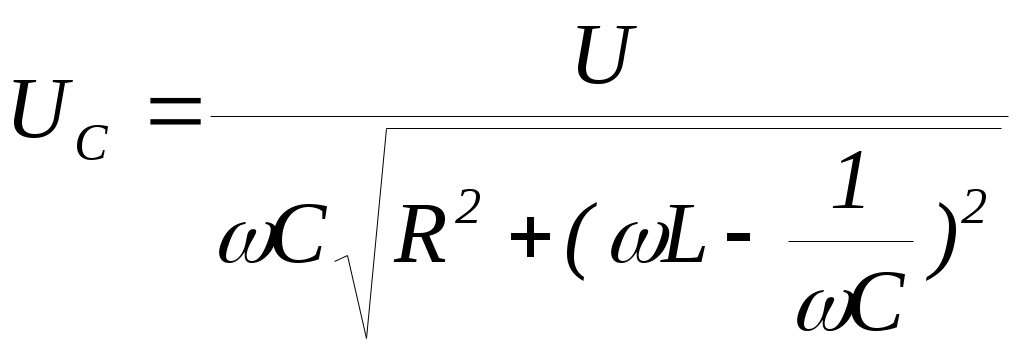 Варианты графиков UL . UC в RLC - цепи 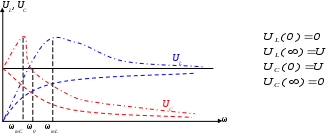  0 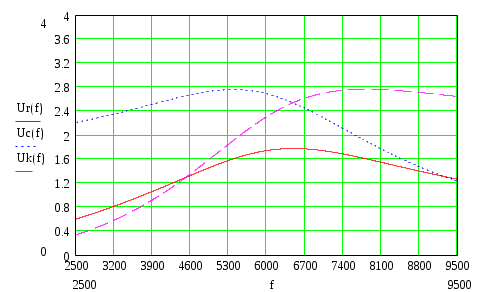 Векторные диаграммы последовательной RLC-цепи Вид диаграмм зависит от выбранной частоты по отношению к резонансной. 1) ω<ω0., UL < UC 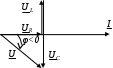  ω=ω0 → UL=UC 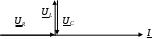 3 φ=0 ) ω>ω0. UL > UC 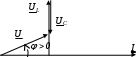 Схема исследования в EWB 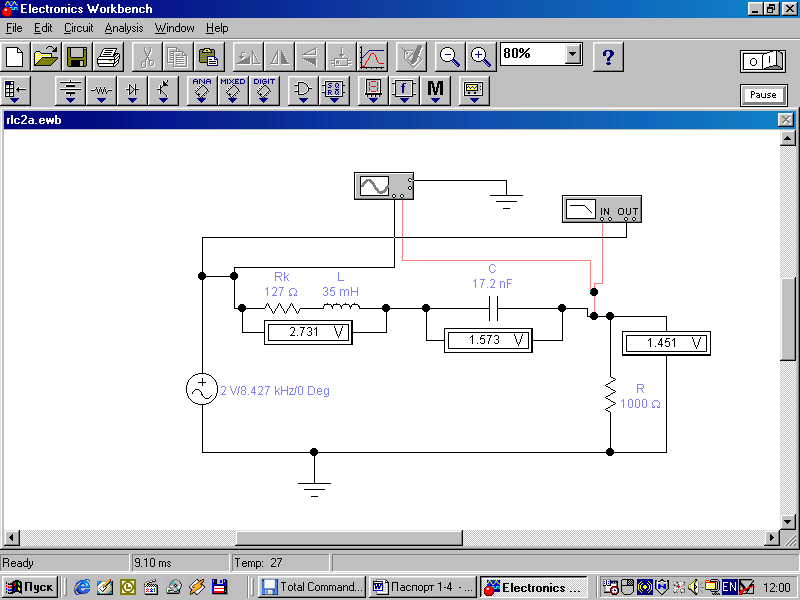 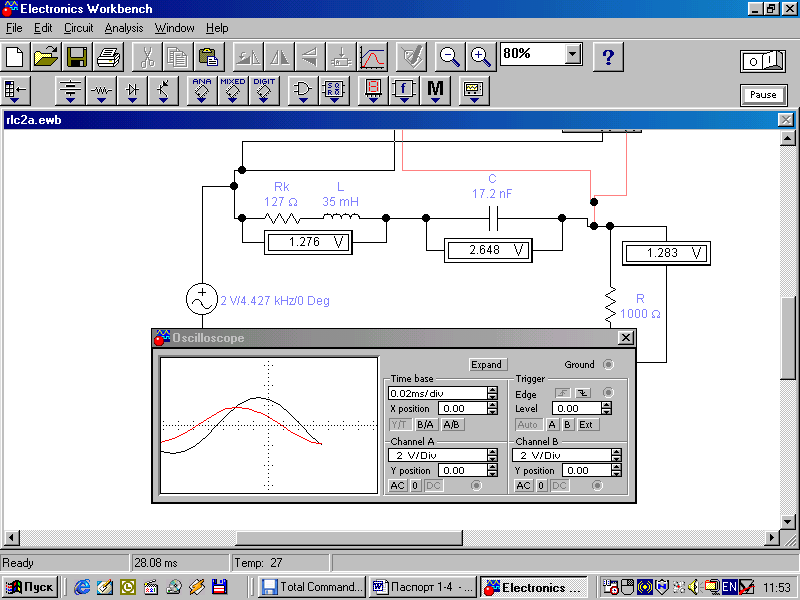  |