ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
6. Резонансные явления и колебательные контуры в электрических цепях§1. Понятие о резонансе в ЭЦ Под резонансом понимают такой режим работы электрической цепи, содержащей RL- и RC-элементы, когда угол сдвига фаз между напряжением и током на какой-то частоте равен 0. Это так называемый фазовый резонанс. Есть амплитудный резонанс, когда достигается максимальная амплитуда колебаний напряжения или тока. Он не является основным для ТЭЦ, основной – фазовый. Резонансная частота определяется по нулевому фазовому сдвигу. 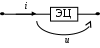 Различают резонанс напряжений, L и C соединены последовательно (индуктивное напряжение компенсируется емкостным) и резонанс токов, L и C – параллельно (индуктивный ток компенсируется емкостным);  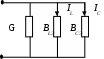 X=0 = XLЭ - XCЭ– резонанс напряжений В=0=BCЭ - BLЭ – резонанс токов §2. Последовательный колебательный контур 1. Основные понятия и параметры ПКК – это электрическая цепь, состоящая из последовательно соединенных катушки индуктивности и конденсатора/ ( резисторов нет, но их иногда включают) П 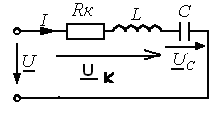 ри анализе ПКК составляют схему замещения: ри анализе ПКК составляют схему замещения:Условие резонанса φ(ωР)=0 (ωРL – 1/ωРC = 0) . Основные параметры: 1) резонансная частота 2) характеристическое сопротивление – это сопротивление реактивного элемента на резонансной частоте 3) добротность – усилительная способность контура, показывающая во сколько раз реактивная энергия в контуре больше активной на резонансной частоте.. 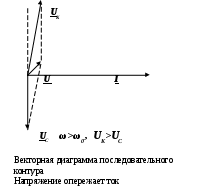 На диаграмме показан вектор тока по горизонтали, вектор напряжения на конденсаторе, отстающий на угол 900, вектор напряжения на катушке индуктивности опережающий ток на угол несколько меньше 900 и вектор общего напряжения, являющийся их суммой. 4) Полоса пропускания П - полоса пропускания –это диапазон частот, где активная мощность поглощаемая контуром не сильно отличается от максимальной поглощаемой мощности (критерий 0.5 от Р0=Р max). Максимальная мощность получается на резонансной частоте, потому что здесь максимальный ток. 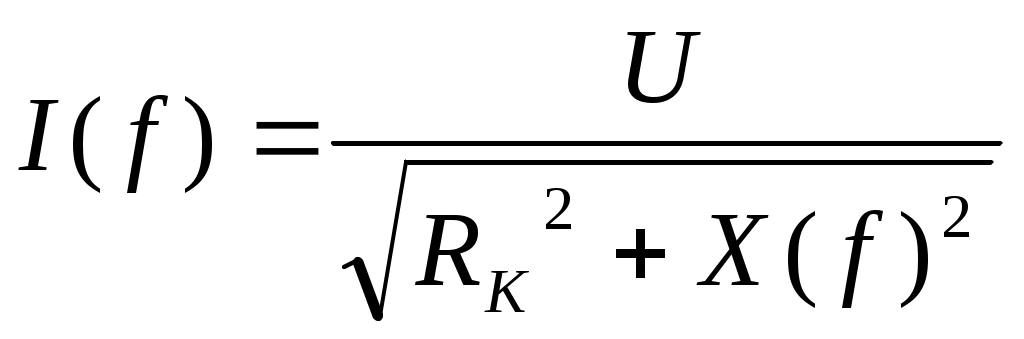 График тока в последовательном контуре носит резонансный характер и ток максимален на резонансной частоте I0(1,2)=Imax =U/RK(1,2) RK2 < RK1 (Q2 > Q1) и I01 < I02 . 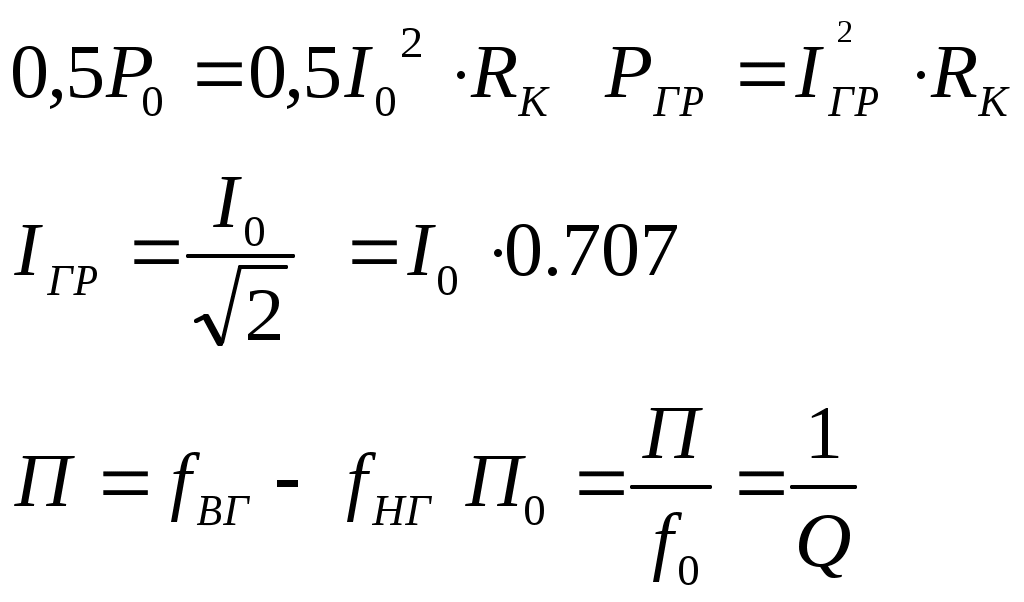  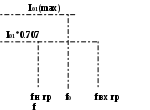 2. Частотные характеристики последовательного контура Зависимость напряжения на катушке и конденсаторе от частоты имеет резонансный характер, причем, если Q>>1, то экстремумы этих напряжений будут почти совпадать с резонансной частотой. Более удобно использовать в контуре нормированные или относительные величины – так легче делить шкалу и соблюдать масштаб. При этом вид графиков сохраняется. I/I0(Р)   η η тем меньше полоса пропускания и круче характеристика.. Можно рассматривать частотные зависимости и для напряжений. . 4. Виды расстроек колебательного контура Под расстройкой понимают отклонение подаваемой на контур частоты от резонансной. 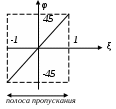 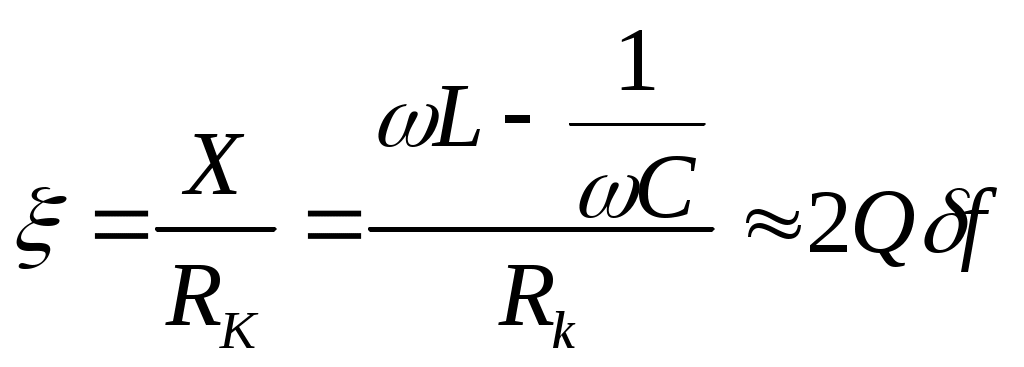 - обобщенная расстройка - обобщенная расстройкаПрактически расчетные формулы для контура определяют через обобщенную расстройку. На границах полосы пропускания обобщенная расстройка равна -1 и +1. UC/UC0 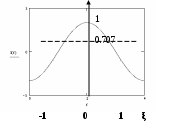 На резонансной частоте UC/UC0=1 ,на границах полосы пропускания 0,707, а обобщенная расстройка равна по абсолютной величине1. Основное предназначение колебательного контура – выделять сигнал нужной частоты, совпадающей с резонансной. Необходима большая избирательность контура и хорошее подавление помех то есть большая крутизна частотных характеристик и следовательно большая добротность. 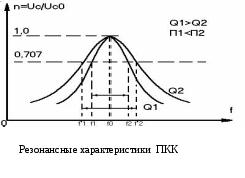 Для оценки избирательности контура вводят понятие коэффициента подавления помехи на частоте помехи КП(fП)=I0/I(fП).≈UC0/UC(fП), где fП - частота помехи ( мешающего сигнала). 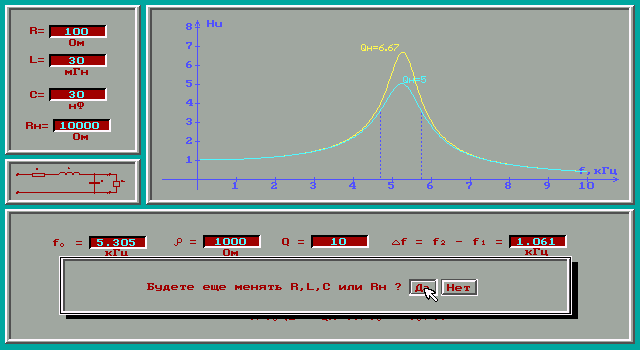 5. Комплексные передаточные функции (комплексные частотные характеристики)  Будем рассматривать линейную электрическую цепь. На вход цепи подключен гармонический источник (воздействие). На выходе рассматривается реакция цепи (отклик на воздействие). Под комплексной передаточной функцией понимают отношение комплексного изображения гармонической реакции ЛЭЦ к комплексному изображению воздействия на цепь. Пусть воздействие Сокращенно функцию T(jω) называют комплексным коэффициентом передачи. Модуль комплексного коэффициента T(ω) представляет собой амплитудно-частотную характеристику (АЧХ). Аргумент комплексного коэффициента передачи АЧХ – это такая характеристика цепи, которая показывает, как изменяется в зависимости от частоты отношение амплитуды реакции (выходного сигнала) к амплитуде воздействия (входного сигнала) при гармоническом воздействии. ФЧХ – это такая характеристика цепи, которая показывает, как изменяется сдвиг фаз выходного и входного сигнала в зависимости от частоты при гармоническом воздействии. Это основные характеристики электрических цепей. Теоретически они рассчитываются с помощью расчетных методов на основе законов Ома и Кирхгофа в комплексной форме. Практически они измеряются с использованием приборов (вольтметров, фазометров, осциллографов). В зависимости от вида реакции и воздействия различают четыре типа передаточных функций: по напряжению (напряжение / напряжение), по току (ток / ток), по сопротивлению (напряжение / ток), по проводимости (ток /напряжение ). Для примера рассмотрим колебательный контур:  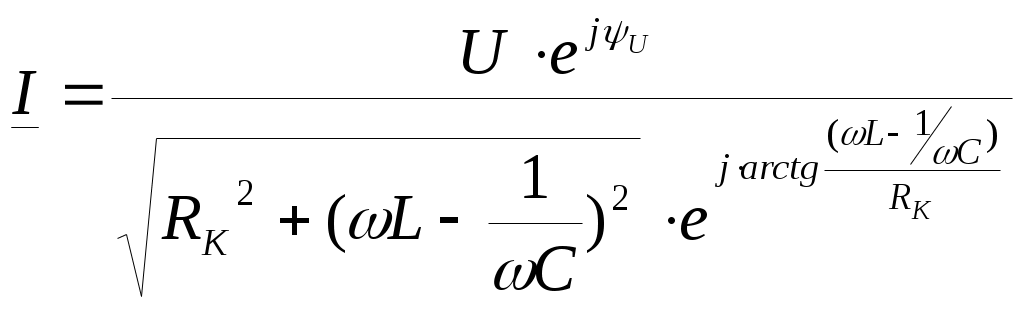 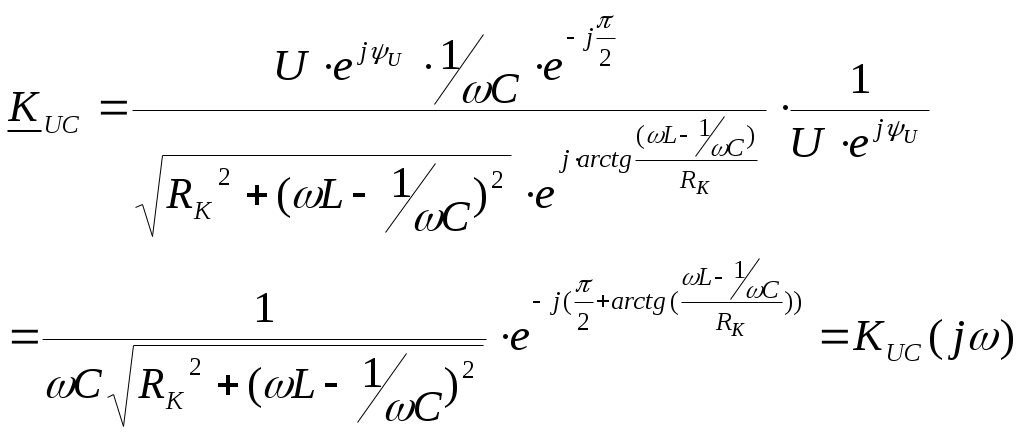 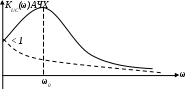 Q>>1 кривая пунктирная при Q<1., при ω=ω0 К0=Q  С использованием расстройки 6. Влияние внешних сопротивлений на избирательность контура (на добротность и полосу пропускания) 1) Влияние внутреннего сопротивления источника 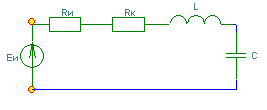 добротность уменьшается, коэффициент подавления помехи добротность уменьшается, коэффициент подавления помехи 2) Влияние сопротивления нагрузки 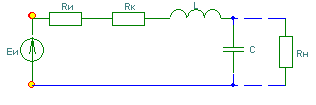 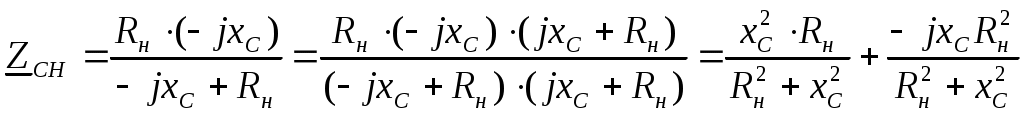 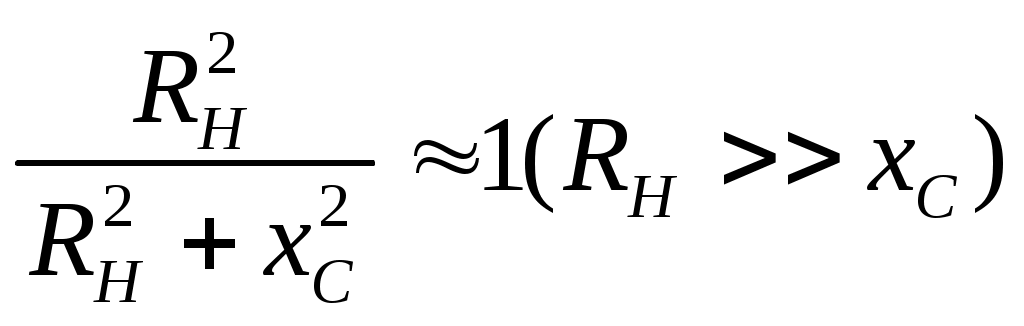 Пример расчета  Рассмотрим графики частотной зависимости напряжения на емкости последовательного контура, так же с учетом сопротивления источника сигнала или нагрузки. 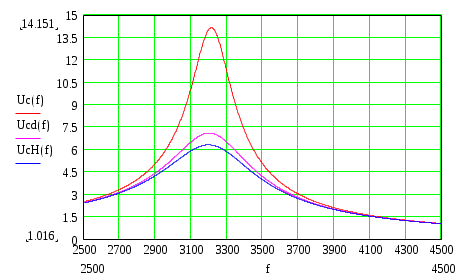 Гц Гц§3. Параллельный колебательный контур 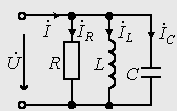 1. Идеализированный контур 1. Идеализированный контури в Q раз больше тока в общей ветви. Поэтому резонанс в параллельном контуре называется резонансом токов. Векторные диаграммы: 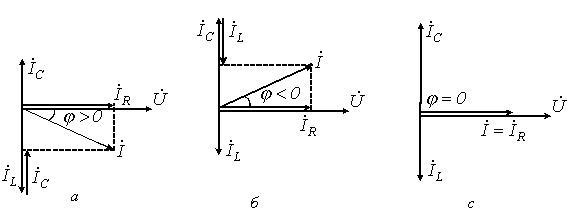 ω < ω0 ω > ω0 ω = ω0 2. Реальный параллельный контур Схема замещения: 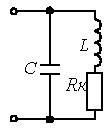 Условие резонанса: 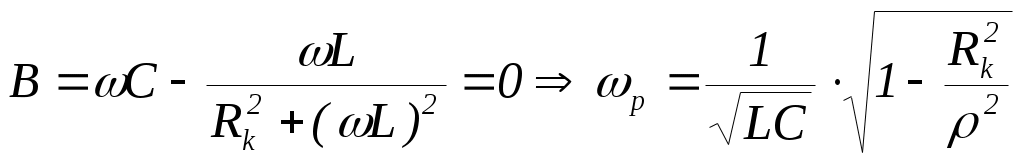 Условие приближения к идеальному контуру: Резонансное сопротивление: 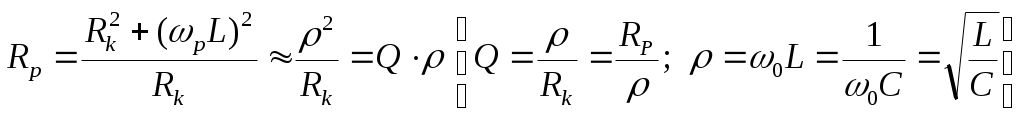 Векторная диаграмма: 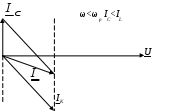 3. Частотные зависимости 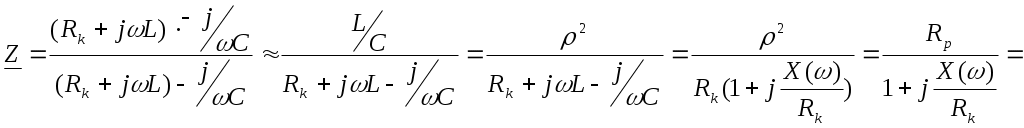 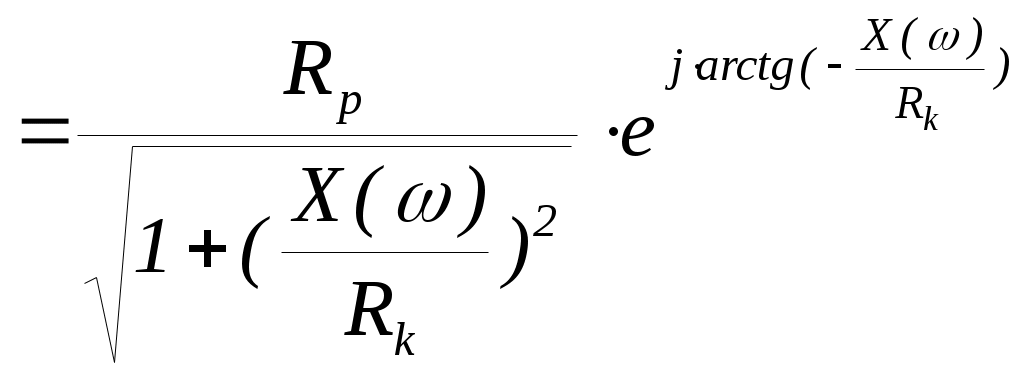 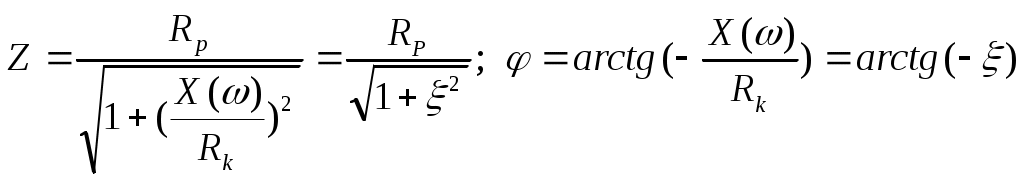 М 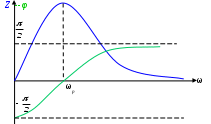 гновенное значение гармонического напряжения гновенное значение гармонического напряжения Из этого следует, что при I=const действующее напряжение на контуре и амплитудное будет повторять зависимостьвеличины Zот (f) . 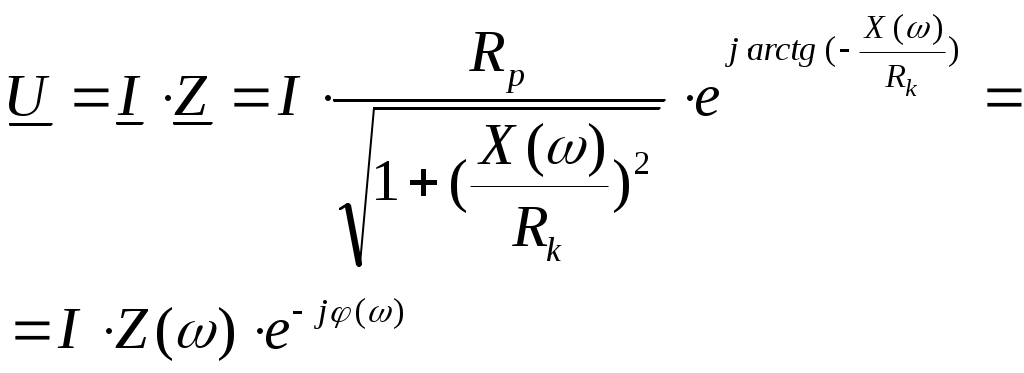 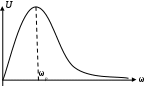 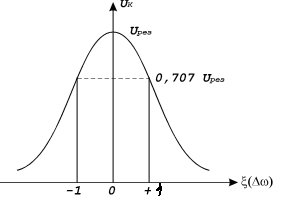 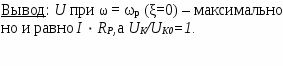 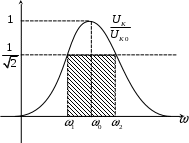 П=ω2 – ω1 Здесь полоса пропускания определяется по уровню 0,707 от максимального значения напряжения на контуре и обобщенная расстройка на границах равна - ,+1. При резонансе (=0) Х=0. Зависимость Х от показана ниже . Параллельный колебательный контур на частоте ниже резонансной (<0) ведет себя как некоторая индуктивность (Х>0), на частоте выше резонансной (>0) – некоторая емкость (Х<0). 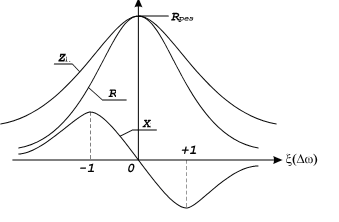 Здесь 4. Влияние внешних сопротивлений на избирательность контура 1) Влияние внутреннего сопротивления источника 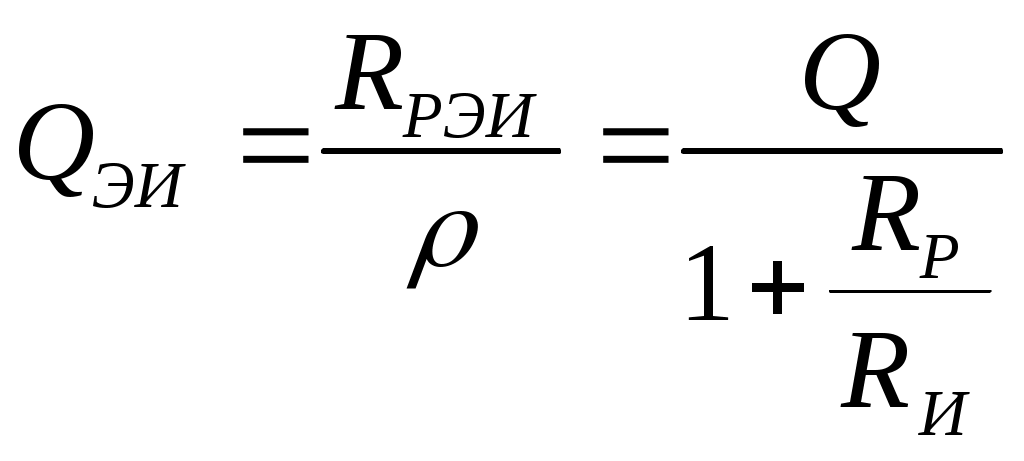 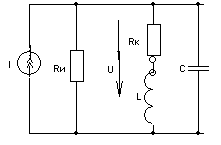 - эквивалентная добротность уменьшается. Избирательные свойства контура ухудшаются, он слабее подавляет помехи. - эквивалентная добротность уменьшается. Избирательные свойства контура ухудшаются, он слабее подавляет помехи.Коэффициент подавления помехи: можно определять и так 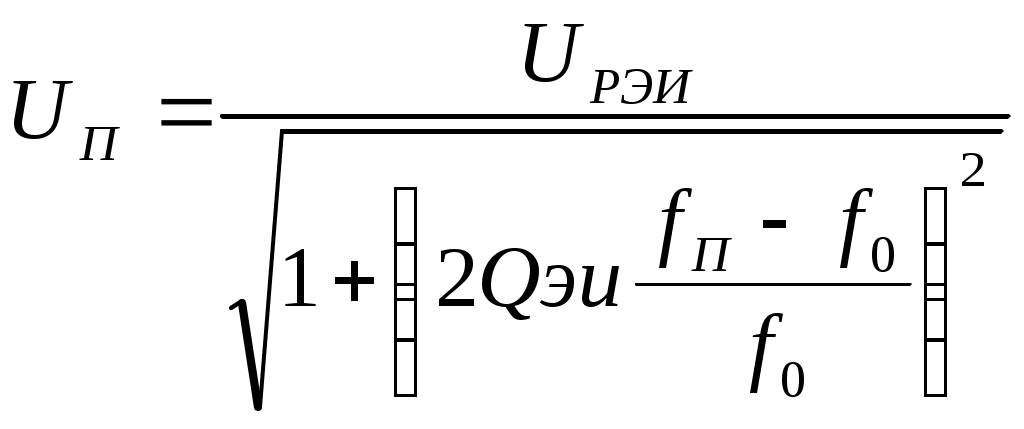 - увеличивается с уменьшением QЭИ и КПП ↓. - увеличивается с уменьшением QЭИ и КПП ↓.2) Влияние сопротивления нагрузки 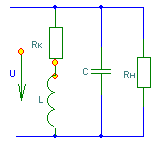 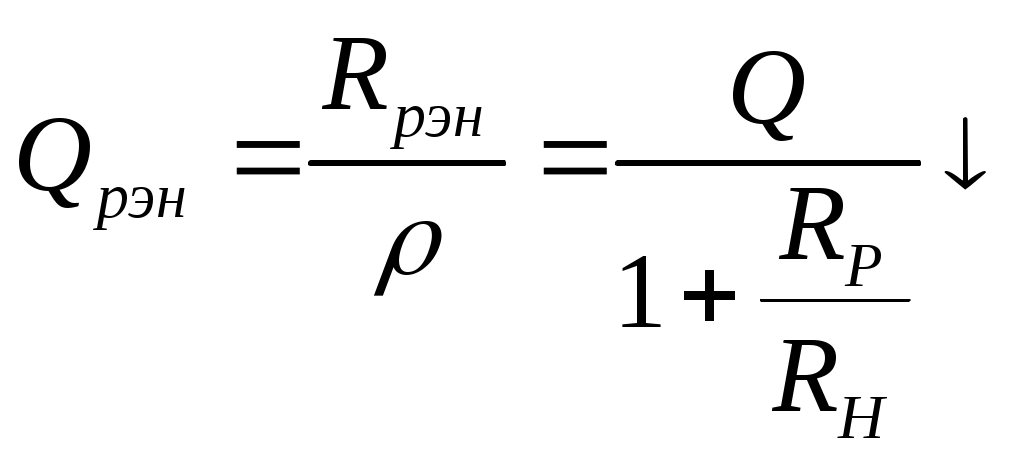 Избирательные свойства ухудшаются, К ПП ↓.. 3) Влияние внутреннего сопротивления источника и сопротивления нагрузки 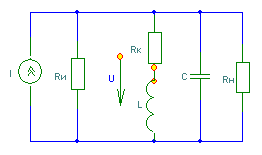 и К ПП ↓. Вывод: Для того, чтобы не ухудшались избирательные свойства контура, необходимо, чтобы RИ, RН>>RР. Либо надо заранее делать контур с большой добротностью. Пример расчета параллельного контура в Mathcad 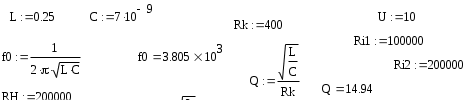 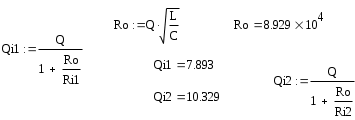 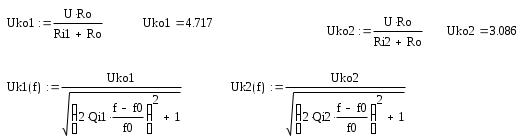 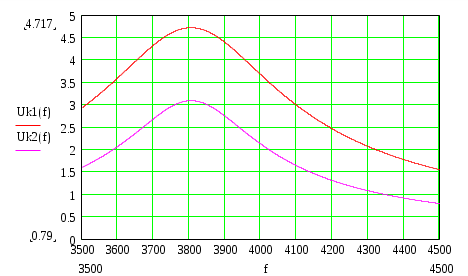 Гц Графики частотных зависимостей напряжения на параллельном контуре Схема исследования параллельного контура в EWB 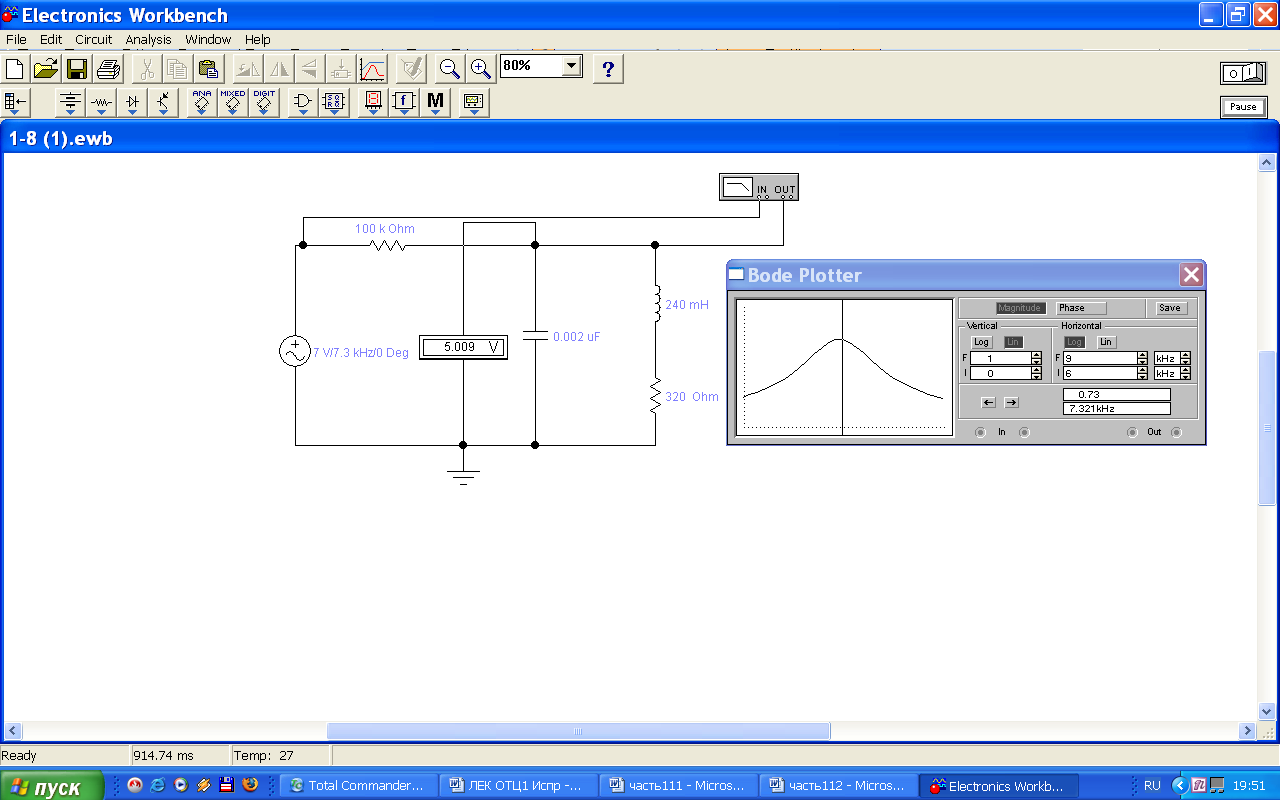 §4. Сложные колебательные контуры 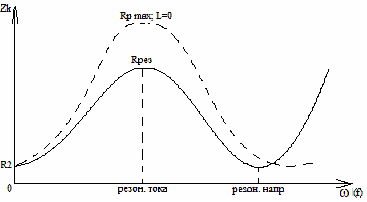 На практике часто используются сложные параллельные контуры для уменьшения резонансного сопротивления, которое в простых контурах достигает десятков и даже сотен килоом, резонансная частота при этом не изменяется. 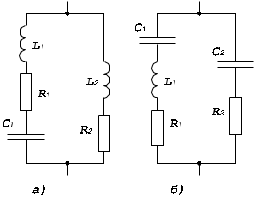 Для параллельного контура с двумя катушками полная индуктивность и полная емкость равны L=L1+L2C=C1. В контуре с двумя конденсаторами – L=L1 Тогда для контура а 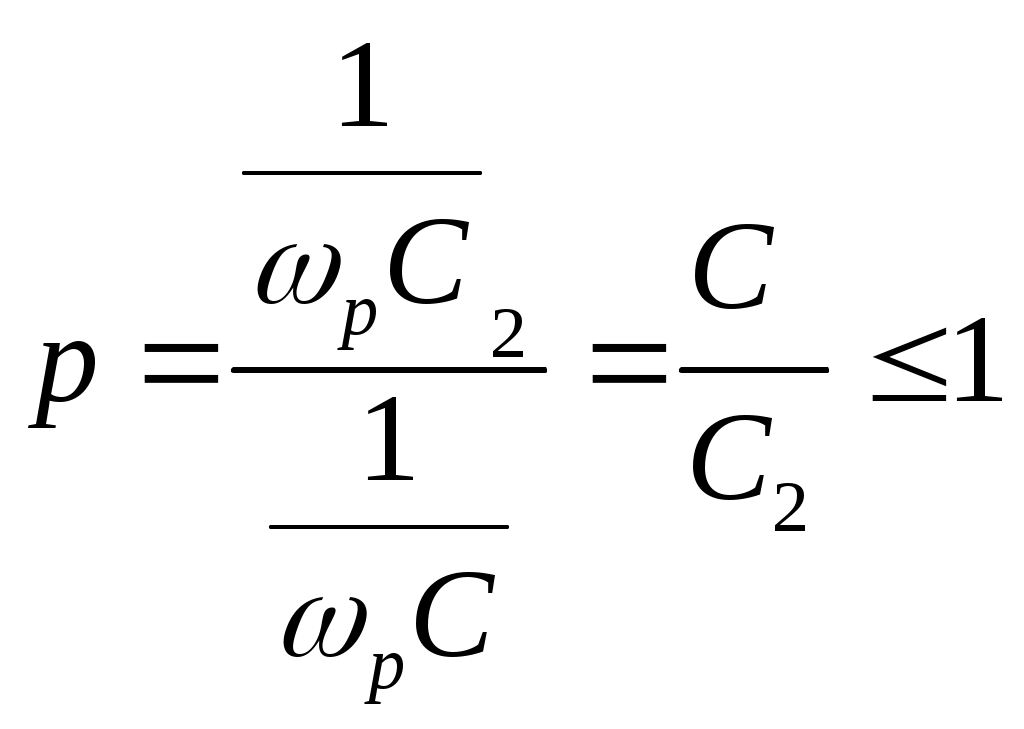 , ,а сопротивление сложного контура на частоте резонанса 1. Контур с двумя индуктивностями 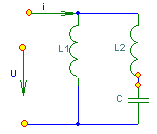 L2 и C соединены последовательно 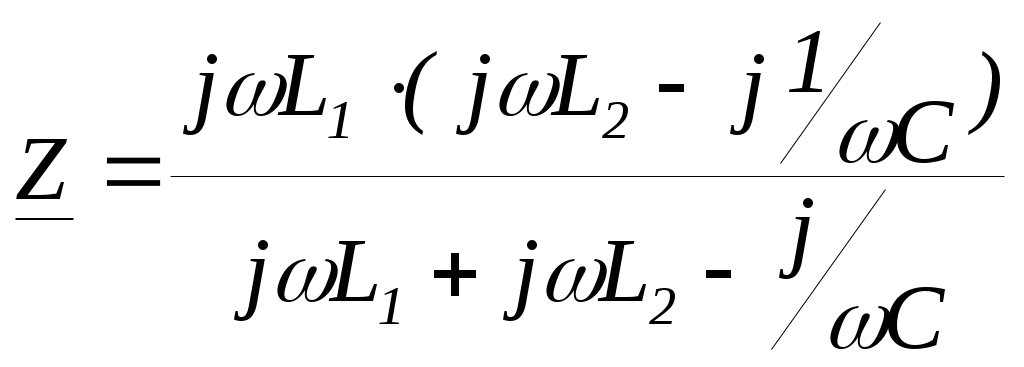 Условие резонанса напряжений: Условие резонанса напряжений: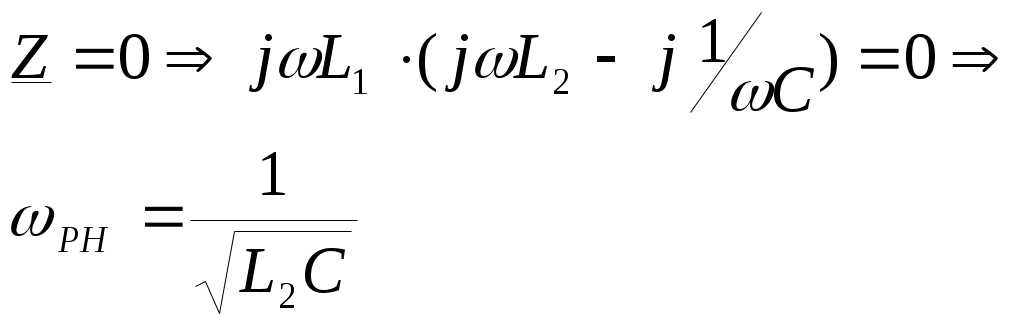  Условие резонанса токов: 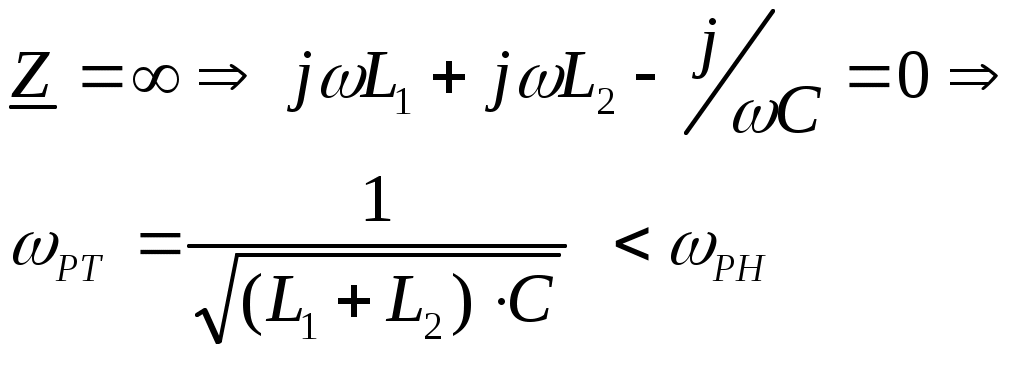 При ω=0 Z(0)=0, При ω= ωРТZ(ωРТ)= ∞ (≈RРЕЗ,) при ω→∞ Z(∞)→∞ 2. Контур с двумя емкостями 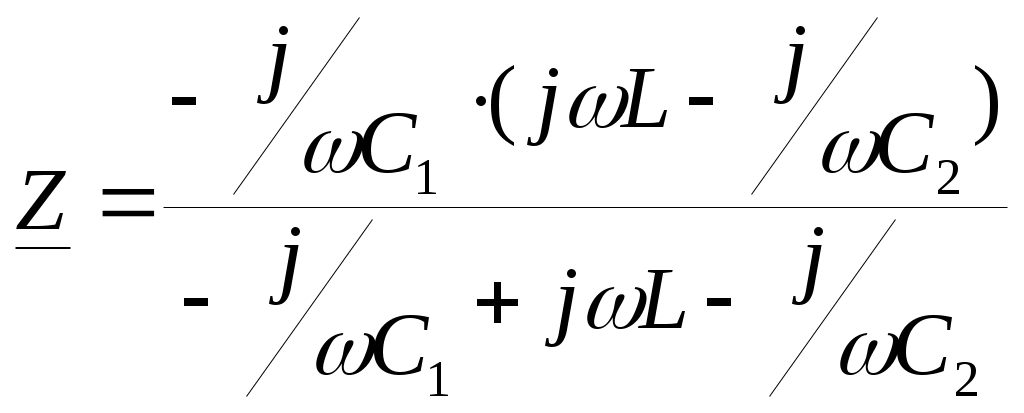 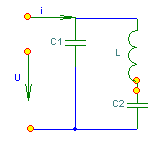 Условие резонанса напряжений: Условие резонанса токов: 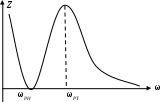 рез напр используется для усиления р рез напр используется для усиления р 0 езонанса контура и лучшего подавления какой то очень мешающей помехи, соответствующей частоте минимума. Пример: приемо-передатчик - рация ( в них бывают режимы работы - симплекс- попеременная работа; дуплекс – одновременная работа) П   ри симплексной работе двух приемо – передатчиков передача сигнала и прием ведется поочередно и на одной частоте.. Это не совсем удобно, но экономично. При дуплексной работе можно одновременно передавать и принимать сигналы, но нужно использовать для передачи и приема разные частоты и f1 Пр = f2 Пер f1 Пер = f2 Пр Сигнал своего передатчика при дуплексном режиме сильно мешает своему приемнику, так как он значительно мощнее и его надо сильнее подавить с использованием сложных контуров. ри симплексной работе двух приемо – передатчиков передача сигнала и прием ведется поочередно и на одной частоте.. Это не совсем удобно, но экономично. При дуплексной работе можно одновременно передавать и принимать сигналы, но нужно использовать для передачи и приема разные частоты и f1 Пр = f2 Пер f1 Пер = f2 Пр Сигнал своего передатчика при дуплексном режиме сильно мешает своему приемнику, так как он значительно мощнее и его надо сильнее подавить с использованием сложных контуров. 3. Контур с двумя емкостями и двумя индуктивностями У данного контура три резонансной частоты: две – резонанса напряжений, одна - резонанса токов. Z(0)=∞ Z(ωPH1,2)=0 (RK) Z(ωPT)=∞(RРЕЗ) Z(∞)→∞. 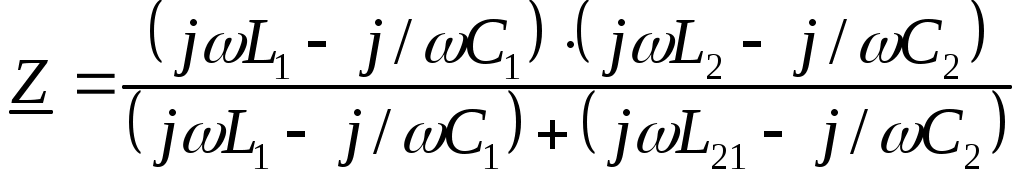 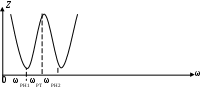 §5. Связанные колебательные контуры 1. Общие понятия Связанными называются такие контуры, которые влияют на резонансные свойства друг друга. Типы связи: взаимно-индуктивная или магнитная (трансформаторная) 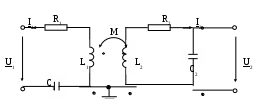 внешняя и внутренняя индуктивная внешняя и внутренняя емкостная 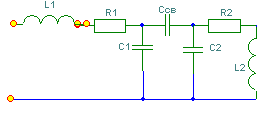 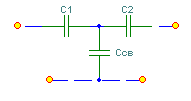 автотрансформаторная 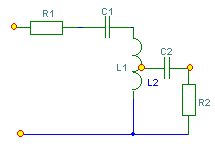 комбинированная 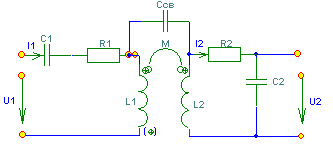 2. Анализ взаимно-индуктивных связанных контуров 1) Уравнения связанных контуров при магнитной связи 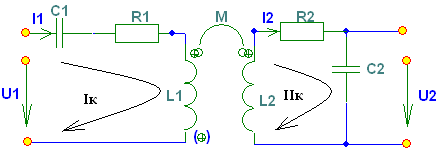 В общем случае анализ проводится в интегральной и дифференциальной форме, а при гармоническом воздействии – в комплексной форме. 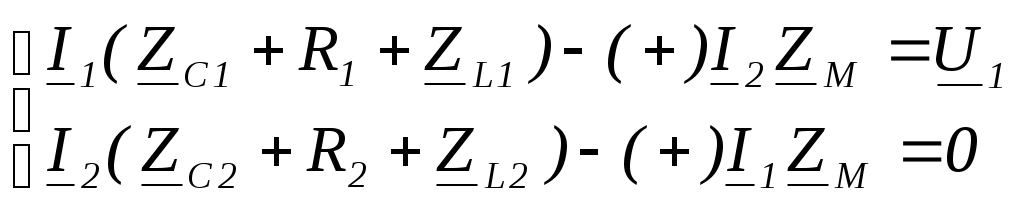 Здесь исходно встречное включение (в скобках – согласное). ZM=jωM Здесь исходно встречное включение (в скобках – согласное). ZM=jωM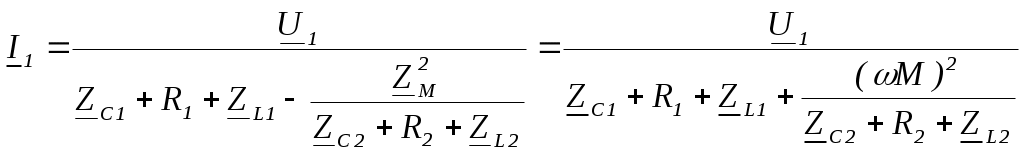 Для упрощения можно обозначить: 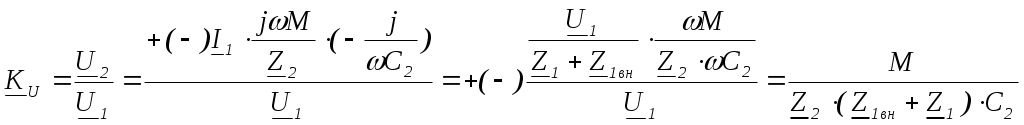 По этой формуле можно определить амплитудно-частотную характеристику. Резонансы в связанных контурах Можно рассмотреть данный вопрос на примере тока 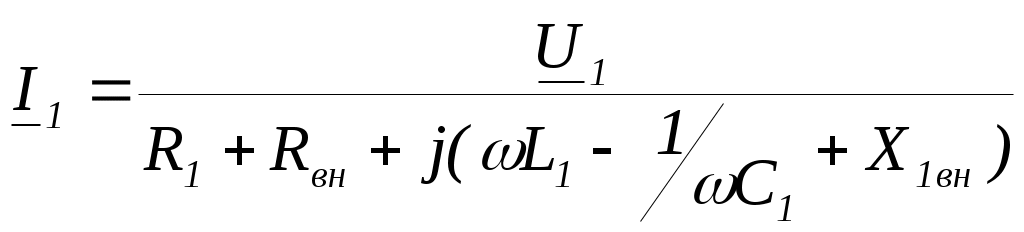 , где , где 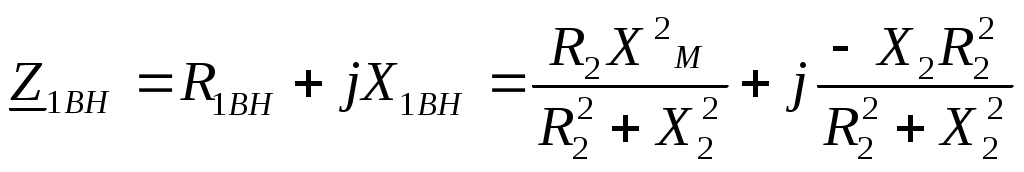 Другой контур оказывает влияние на резонанс, т.к. резонансная частота будет определяться соотношением: Одинаковые собственные (без влияния) частоты контуров, т.е. ω01=ω02. Не одинаковые ω01 ≠ ω02. Первый вариант чаще применяется. X1ВН(ω0)=0 Резонанс в системе связанных контуров достигается соответствующей их настройкой. Первый частный резонанс обеспечивает максимум тока I1 и достигается настройкой контура 1 до обеспечения условия: Второй частный резонанс обеспечивает максимум тока I2 и достигается настройкой контура 2 до обеспечения условия: 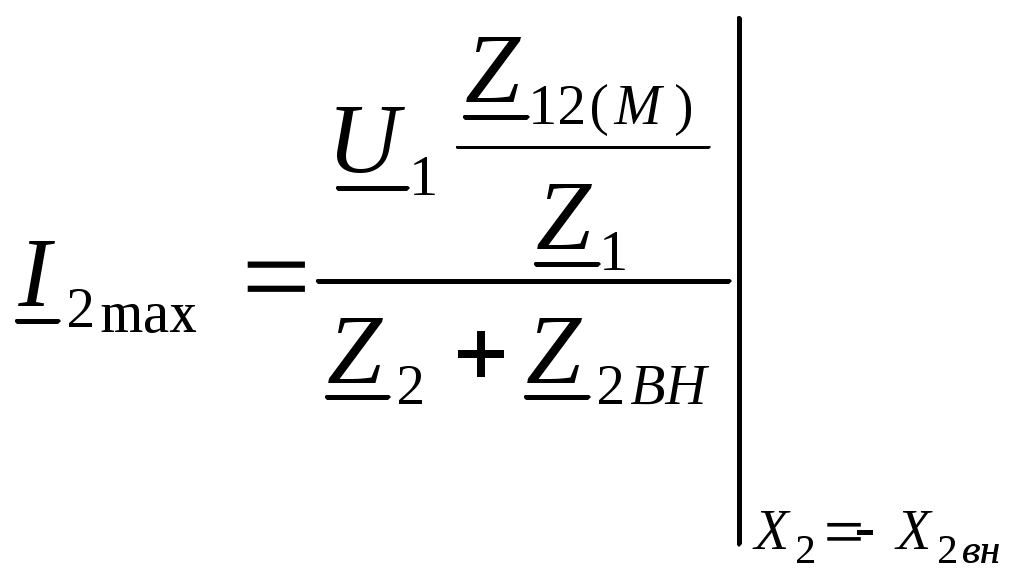 , , 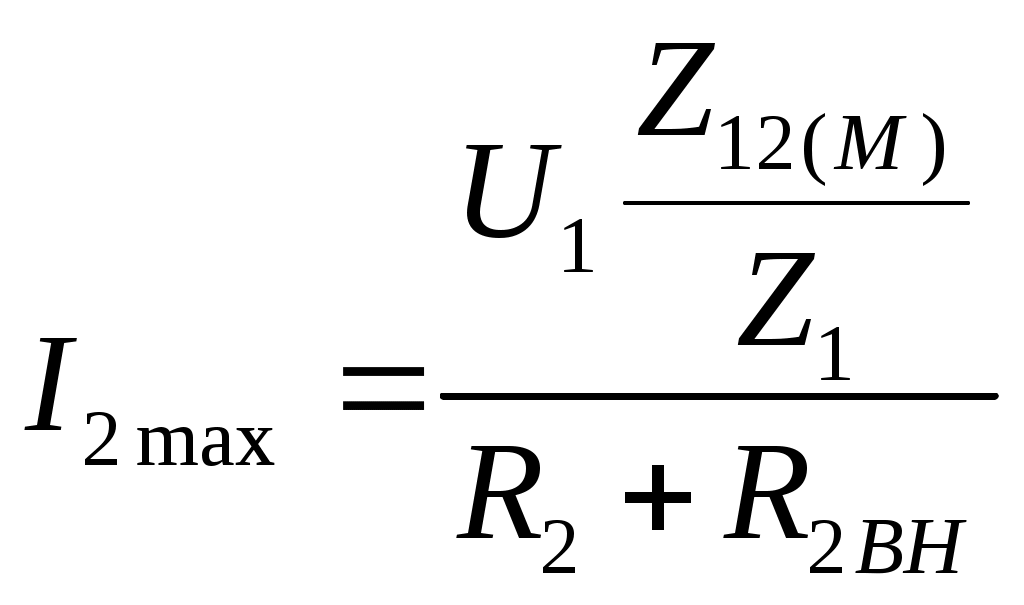 . . Сложный резонанс осуществляется путем настройки каждого контура на частный резонанс и подбором оптимального сопротивления связи: 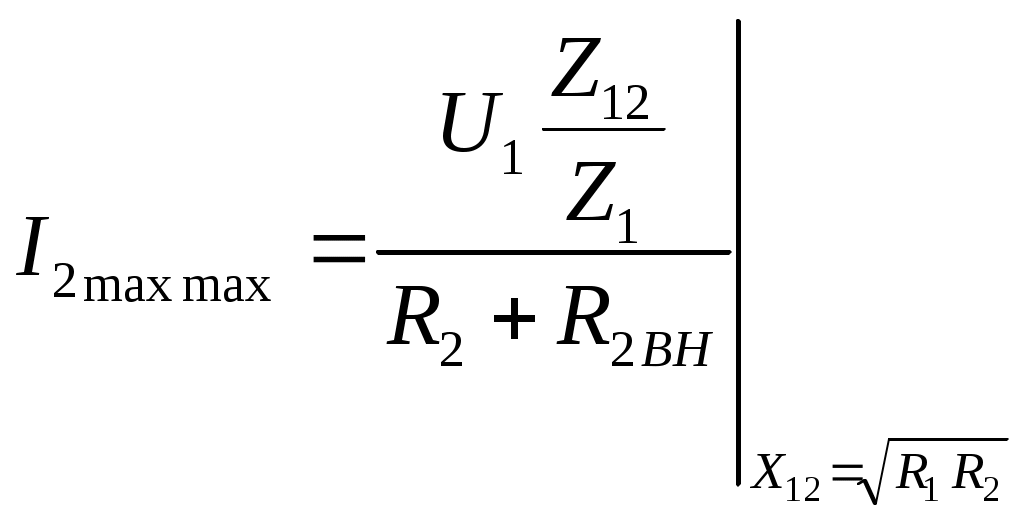 , где , где 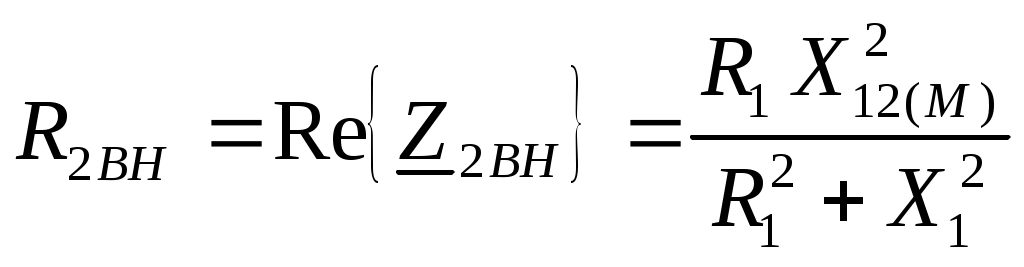 . .Далее 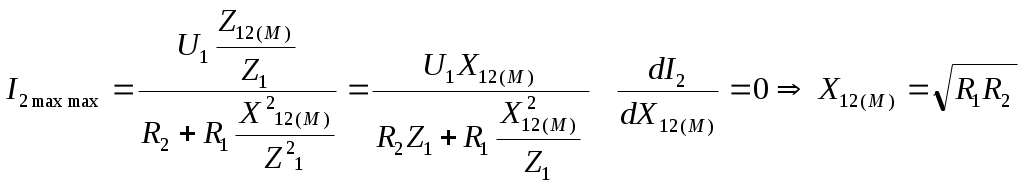 Окончательно получаем: Полный резонанс достигается настройкой каждого контура в индивидуальный резонанс 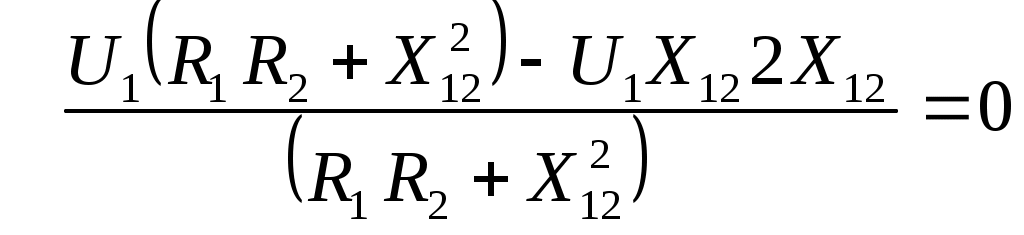 .и .и Максимальная мощность выделяется во 2 контуре при максимуме тока в нем, поэтому среди частотных характеристик наибольший интерес представляет зависимость Ток в контуре 2 Пусть 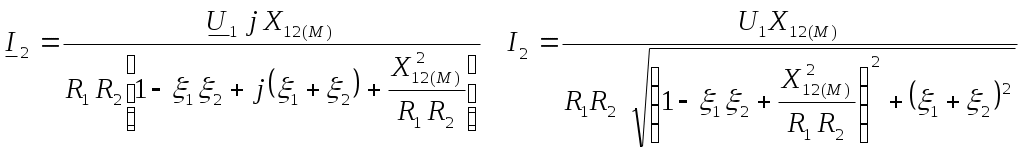 . .При 0 расстройке Х1 и Х2 равны 0, ток будет иметь экстремум – максимум или минимум. Это зависит от сопротивления связи Х12=ωМ и Часто рассматривают относительные характеристики вида I2/I2mm. Здесь I2mm – максимальное из всех максимальных значений. Здесь можно выделить слабую связь, оптимальную или критическую, сильную и сверхсильную связи. При слабой связи ωM – мало, т.е. M – мало. Тогда вносимое сопротивление тоже небольшое и не сказывается на характеристиках – они практически такие же, как у одиночного контура. Если связь оптимальная или критическая, то вносится некоторое среднее сопротивление. Частотная характеристика становится более прямоугольной и полоса пропускания становится несколько больше чем у одиночного контура 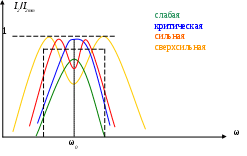 ,707 от максимума). Для разговорной речи достаточно узкой полосы пропускания (300 – 3400 Гц). Широкая полоса пропускания требуется, например, для сигнала музыкального (100 – 15000 Гц). ,707 от максимума). Для разговорной речи достаточно узкой полосы пропускания (300 – 3400 Гц). Широкая полоса пропускания требуется, например, для сигнала музыкального (100 – 15000 Гц).Анализ частотных характеристик связанных контуровРассмотрим ток при одинаковых контурах (ξ1=ξ2=ξ) 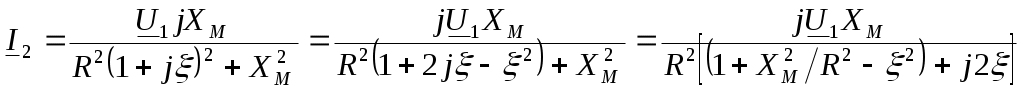 . .Модуль последнего выражения 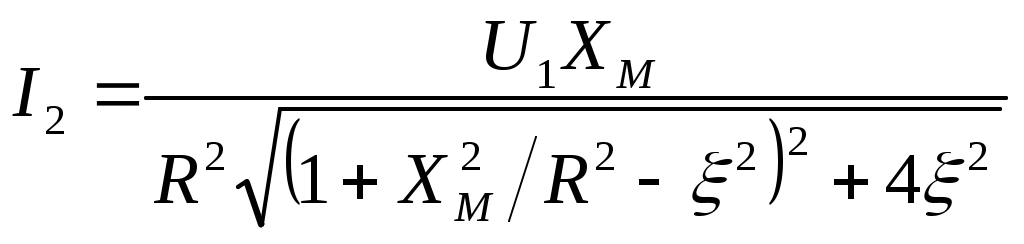 . .Введем обозначения (при р) До множим и разделим на pL и учтем, что добротность контура Максимально возможный ток второго контура при одинаковых контурах (R1=R2=R) равен Нормированная амплитудно-частотная характеристика связанных контуров 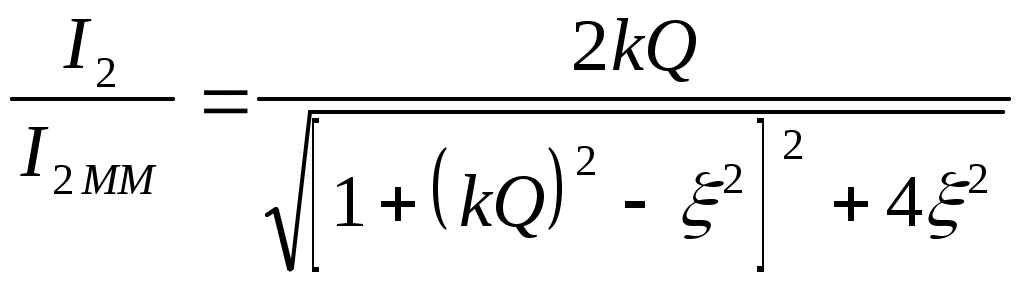 . . Рассмотрим вид зависимости при различных значениях kQ. Величина kQ называется фактором связи. Слабая связь 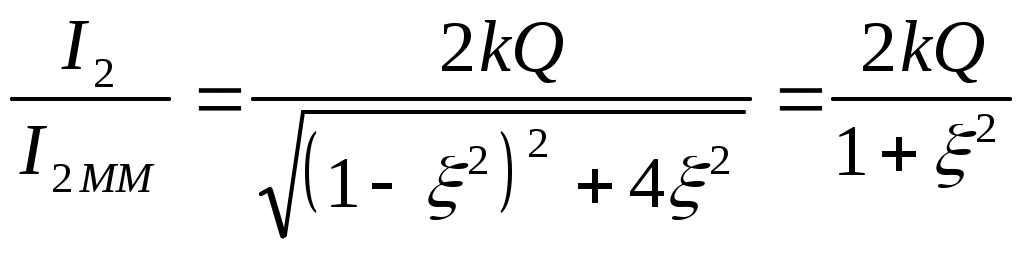 . . Амплитудно-частотная характеристика достигает максимума при =0 (рис. ). Значение тока при резонансе тем больше, чем больше фактор связи kQ, но 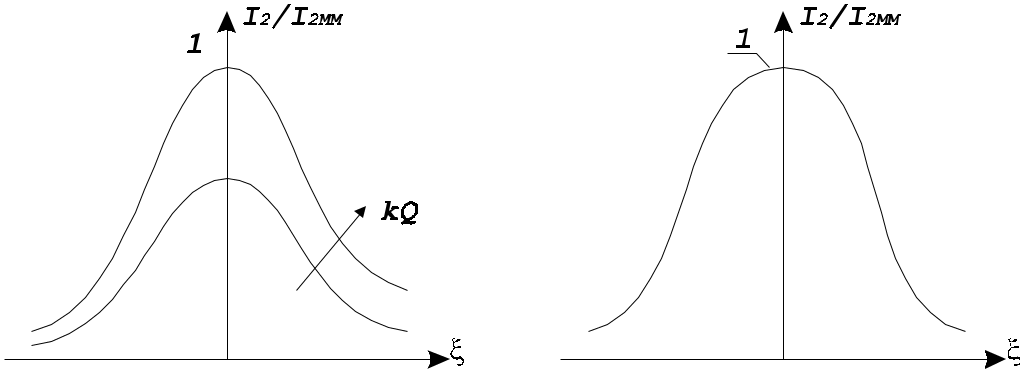
Критическая связь kQ=1. Подстановка kQ=1 в приводит к выражению Полоса пропускания по уровню 0,707 системы связанных контуров при критической связи Сильная связь kQ>1. В этом случае для амплитудно-частотной характеристики надо пользоваться общим выражением . Если исследовать на экстремумы, т.е. 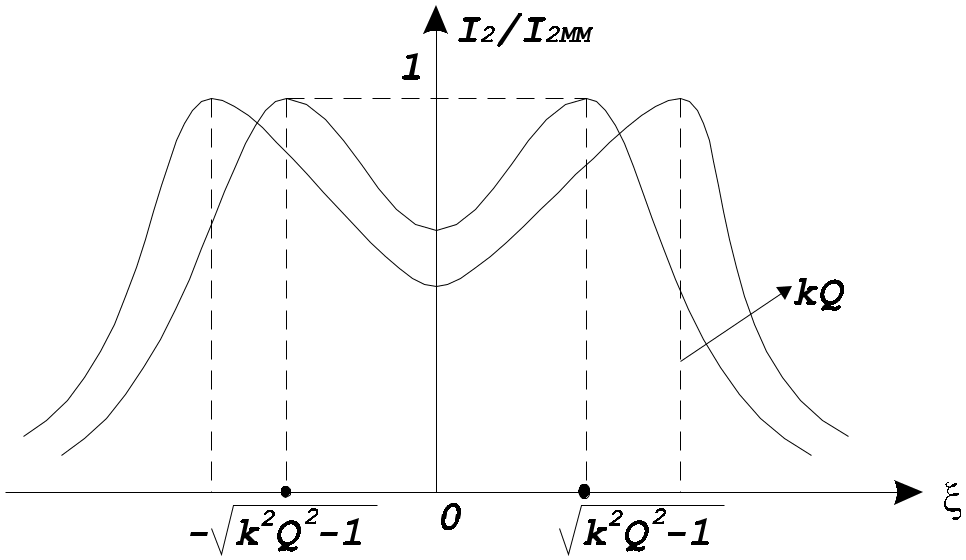 Амплитудно-частотная характеристика системы связанных контуров с ростом фактора связи kQ меняется от одногорбой до двугорбой , крутизна склонов кривой возрастает, характеристика расширяется. При слабой связи максимум тока I2 наступает на частоте р – резонансной частоте контура при сильной связи кривая тока имеет два максимума на частотах (частотах связи), определяемых из условия 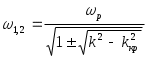 , , где При слабой связи и при идентичных контурах относительная полоса пропускания 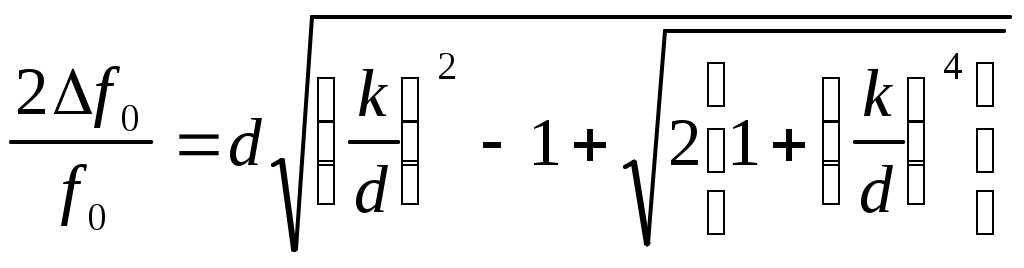 . . При критической связи и идентичных контурах относительная полоса пропускания 3. Практическое применение Применяются в радио-, телевизионных приемниках для получения характеристики, близкой к идеальной (прямоугольной) для выделения полосы частот сигнала нужной средней частоты. Чаще используется несколько связанных контуров 3 – 5 ( Фильтры сосредоточенной селекции - ФСС в усилителе промежуточной частоты – УПЧ, здесь осуществляется основная селекция и усиление принимаемого сигнала, начальная селекция осуществляется во входных цепях радиоприемников перестраиваемыми контурами, связанные контуры сложно сделать с перестройкой резонанса). |
