ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г

• Название: Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
• Дата: 24.09.2022
• Размер: 3.24 Mb.
• Имя файла: Лекции по ОТЦ Часть 1.doc
• Тип: Конспект лекций; #693470
• страница: 2 из 8

2. Основные Понятия и определения в ОТЦ

2.1. Классификация цепей, режимы их работы

Электромагнитные процессы, протекающие в электротехнических устройствах (ЭТУ), как правило, достаточно сложны. Однако во многих случаях, их основные характеристики можно описать с помощью таких интегральных понятий, как: напряжение, ток, электро­движущая сила (ЭДС).

Совокупность деталей электротехнического устройства, соединенных проводниками и предназначенная для протекания тока называют электрической цепью (ЭЦ). Совокупность цепей разных ЭТУ образуют сложную ЭЦ.

Такая цепь состоит из отдельных частей (объектов), выполняющих опреде­ленные функции и называемых элементами цепи. Основными элементами цепи являются источники и приемники электрической энергии (сигналов). Электротехнические устрой­ства, производящие электрическую энергию, называются генераторами или источни­ками электрической энергии, а устройства, потребляющие ее – приемниками (потреби­телями) электрической энергии.

В цепи могут действовать различные виды источников электрической энергии: пер­вичные (батареи, аккумуляторы, механические генераторы) и вторичные (выпрямители, преобразователи разных видов эл. энергии).

Классификация электрических цепей

• 
  Линейные и нелинейные цепи
  

Линейные цепи – это цепи, свойства которых не зависят от величин, направлений токов и напряжений в участках цепи, в них соблюдаются принципы пропорцио­нальности и суперпозиции (наложения). В нелинейных цепях свойства зависят от величин токов и напряжений. При этом линейные цепи описываются линейными уравнениями, нелинейные – нелинейными.

• 
  Стационарные и нестационарные цепи
  

Стационарными называются цепи, в которых не происходит никаких изменений. Нестационарные цепи – это цепи, которые сами меняются.

Режимы работы ЭЦ

Различают установившийся или стационарный режим работы электрической цепи (когда процессы в ней описываются стационарными функциями (постоянные величины или пе­риодически изменяющиеся)) и переходной режим работы (переход от одного стационар­ного режима к другому, где другие токи и напряжения; Переходный режим. начинается после каких-то рез­ких изменений в ЭЦ, которые обеспечиваются срабатыванием коммутацион­ных элементов).

2.2. Основные электрические величины

• 
  Электрический ток
  

I – постоянный ток

i(t) – мгновенное значение меняющегося тока



[i(t)]=A - основная единица, (mA - кратная)

• 
  Напряжение
  

U – постоянное напряжение

u(t) – мгновенное значение меняющегося напряжения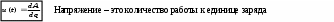



[u(t)]=B, mB

• 
  Мощность
  

p(t) – мгновенное значение изменяющейся мощности, Р – постоянная мощность.



[p(t)]=B·A

• 
  Электрическое сопротивление проводника R
  

[R]=Ом, кОм

Все расчеты с использованием электрических величин делаются в основных величинах.

2.3. Основные элементы ЭЦ

Для исследования процессов в электрических цепях в теории вводят понятие идеаль­ных элементов ЭЦ – это такие элементы, которые обладают одним конкретным свойством и описываются одним уравнением (бывают исключения).

Все элементы электрической цепи условно можно разделить на активные и пассивные. Активным называется элемент, содержащий в своей структуре источник электрической энергии. К пассивным относятся элементы, в которых рассеивается (резисторы) или нака­пливается (катушка индуктивности и конденсаторы) энергия. К основным характеристи­кам элементов цепи относятся их вольт-амперные, вебер-амперные и кулон-вольтные ха­рактеристики, а также связь между электрическими величинами, описываемые дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются линейными дифференциальными или алгебраическими уравнениями, то они называются линейными, в противном случае они относятся к классу нелинейных. Строго говоря, все элементы являются нелинейными. Возможность рас­смотрения их как линейных, существенно упрощает математическое описание и ана­лиз процессов, определяется границами изменения характеризующих их переменных и их частот. Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях, называются параметрами элемента.

Пассивные элементы

Рассмотрим пассивные элементы цепи, их основные характеристики и параметры.

1. 
   Резистивный элемент (резистор)
   

Условное графическое изображение резистора приведено на рис. 1,а. Требуется заметить, что в резистивном эле­менте происходит превращение электрической энергии в тепловую и, следовательно, рассеяние ее (уход из цепи)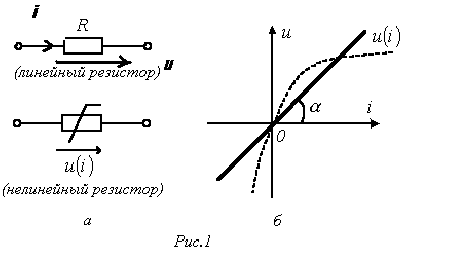


Резистор – это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее опре­деляется геометрическими размерами элемента и свойствами материала: удельным сопротив­лением ρ (Ом▪м) или обратной величиной – удельной проводимостью g= ρ ^-1 (См/м). В простейшем случае проводника длиной l и сечением S его резистивное (активное) сопротивление определяется выражением (Ом – основная единица и кОм, Мом -кратные). В общем случае определение сопротивления связано с расче­том ‘электромагнитного поля в проводящей среде, разделяющей два электрода. Основной характеристикой ре­зистивного элемента является зависимость u(i)(или i(u)), называемая вольтамперной ха­рактеристикой (ВАХ). Если зависимость u(i) представляет собой прямую линию, прохо­дящую через начало координат (см. рис. 1,б), то резистор называется линейным и описы­вается соотношением закона Ома:

или ,

где G=R^-1 – резистивная (активная) проводимость. .

При этом R=const. Нелинейный резистивный элемент, ВАХ ко­торого нелинейная (рис. 1,б), как будет показано в блоке лекций, посвященных нелиней­ным цепям, характеризуется несколькими параметрами. Для линейного резистивного элемента справедливы следующие равенства: между напряжением и током Для мощности в резисторе можно записать выражение

, которое неотрицательно, так как R>0 (резистор все время поглощает электрическую энергию преобразуя ее в тепловую)
2. Индуктивный элемент (катушка индуктивности) Данный элемент является накопителем энергии и создает сильное магнитное поле..

Условное графическое изображение катушки индуктивности приведено на рис. 2,а. Ка­тушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета индук­тивности катушки необходимо рассчитать созданное ею магнитное поле. Индуктивность определяется отношением потокосцепления к току, протекающему по виткам ка­тушки: 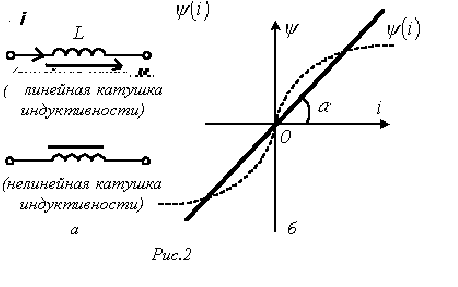Используются и кратные единицы мГн, мкГн/ В свою очередь потокосцепление равно сумме произведений потока, прони­зывающего витки, на число этих витков



Основной характеристикой катушки индуктивности является зависимость ψ(i), называе­мая вебер-амперной характеристикой. Для линейных катушек индуктивности зависимость ψ(i) представляет собой прямую линию, проходящую через начало координат (см. рис. 2,б); при этом L=const. Нелинейные свойства катушки индуктивности (см. кривую ψ(i) на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала, для кото­рого зависимость магнитной индукции от напряженности поля нелинейная.

Если элемент линейный, то справедливы следующие равенства: между током и напряжением индуктивного элемента , , Мощность в индуктивности и индуктивность в одни моменты времени поглощает электрическую энергию в другие отдает. Требуется заме­тить, что в катушке индуктивности электрическая энергия переходит в энергию маг­нитного поля. При i_L=const=I_L

u_L=U_L=0 и индуктивный элемент не оказывает сопротивление постоянному току.

3. Емкостный элемент (конденсатор) Основное его свойство –накапливать энергию и создавать сильное электрическое поле.

Условное графическое изображение конденсатора приведено на рис. 3,а. Конденса­тор – это пассивный элемент, характеризующийся емкостью. Для расчета последней необ­ходимо рассчитать электрическое поле в конденсаторе. Емкость определяется отноше­нием заряда q на обкладках конденсатора к напряжению u между ними: и зави­сит от геометрии обкладок и свойств диэлектрика, находящегося между ними. 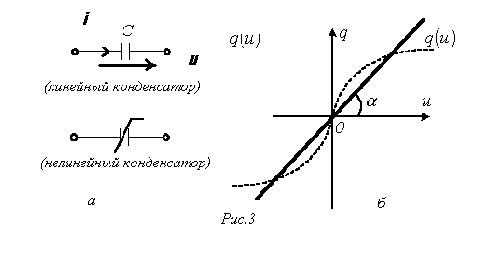Используют и кратные единицы мкФ, нФ, пФ. Большин­ство диэлектриков, используемых на практике, линейны, т.е. у них относительная диэлек­трическая проницаемость ε =const. В этом случае зависимость q(u) представляет собой прямую линию, проходящую через начало координат, (см. рис. 3,б) и C=const



. Если элемент не меняется во времени, то справедливы следующие равенства: , . Данный эле­мент также является накопителем энергии. При u_C=Uc=const i_c=I_c=0 Емкость не пропускает постоянный ток

Таким образом, всего существует три пассивных элемента – резистивное сопротивле­ние, индуктивность и емкость. Каждый элемент характеризуется основными уравнениями.
Активные элементы

Рассмотрим активные идеальные элементы (источники энергии) цепи.

Определение: Идеальный источник напряжения – это такой источник электрической энергии, напряжение на зажимах которого не зависит от тока, протекающего через его за­жимы и является некоторой заданной функцией данного источника. Причем эта функция

не меняется, куда бы ни включался данный источник и сколько бы времени он ни работал.

Напряжение на зажимах такого источника равно ЭДС.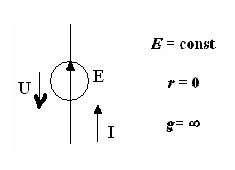




В общем случае ЭДС меняется во времени е(t)
Определение: Идеальный источник тока – это такой источник электрической энергии, ток через зажимы которого не зависит от напряжения на его зажимах, а является заданной функцией данного источника, которая не меняется, куда бы ни включался и сколько бы времени ни работал источник. В общем случае ток меняется во времени j(t)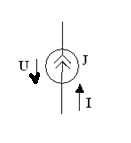



Такие источники называют независимыми. Есть еще зависимые или управляемые источ­ники – это такие, параметры которых зависят от токов и напряжений в каких-то участках цепи.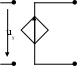


e_у (t)=фун(u_у) – источник напряжения, управляемый

напряжением (ИНУН), например e_У =k▪u_У.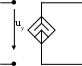

j_у (t)=фун(u_у) – источник тока, управляемый

напряжением (ИТУН). Существуют ИТУТ и ИНУТ.

2.4. Модель и схема ЭЦ

Под моделью ЭЦ понимают идеализированную электрическую цепь, составленную из идеальных элементов, отражающую основные процессы, происходящие в реальной ЭЦ. Каждый участок реальной ЭЦ или деталь моделируется так называемой схемой замеще­ния.

Основные детали, узлы ЭЦ имеют собственные схемы замещения, которые отражают их свойства. В общем случае под схемой понимают условное графическое изобра­жение ЭЦ.

Выделяют следующие разновидности схем:

• 
  Принципиальная ЭС. В такой схеме каждый элемент (деталь) цепи обозначается стандарт­ным условным изображением без раскрытия внутренних свойств. На таких схемах не показано расположение элементов в пространстве, а только указано как соеди­нены элементы проводниками.
  
• 
  Монтажные ЭС. Такие схемы используются для показа пространственного располо­жения. В них в ряде случаев эскизно изображается реальный вид детали.
  
• 
  Расчетные эквивалентные ЭС. Такие схемы используются для расчета ЭЦ. Каждая де­таль цепи показывается схемой замещения, т.е. моделью.
  

Схемы замещения реальных деталей ЭЦ

1. 
   Реальный резистор
   

Первый уровень схемы замещения – резистивное сопротивление, отражает потери энергии внутри резистора

Н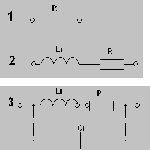
а втором уровне учитывают, что при протекании тока вокруг проводника создается магнитное поле, которое можно характеризовать некоторой малой индуктивностью – L_R . Также есть электрическое поле между выводами резистора, что отражают малой емкостью на третьем уровне моделирования.


R – сопротивление резистора основной параметр;

L_R –индуктивность резистора – не основной (паразитный) параметр

C_R – емкость резистора - не основной параметр. Здесь каждый элемент описывается соответствующим уравнением и получается много уравнений.

2) Катушка индуктивности - аналогично рассматривают и процессы здесь.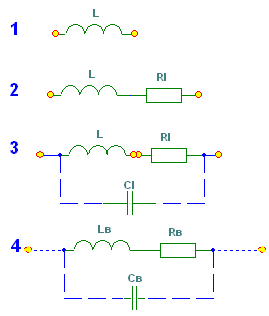





R_L – сопротивление проводов катушки.

С_L – эквивалентная емкость катушки

На последнем этапе каждый виток катушки представляют такой схемой замещения.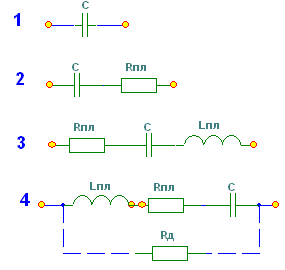





3) Конденсатор
R_пл. – сопротивление пластин;

R_д – сопротивление диэлектрика между пластинами

Lпл – индуктивность пластин
Чем сложнее модель, тем точнее она отражает процессы в реальной детали, но соответственно тем сложнее математическое описание и труднее делать вычисления и расчеты по такой модели. Выбор модели определяется соотношением между точностью и сложностью расчетов.

Схемы замещения источников электрической энергии

Реальные источники электрической энергии по своим свойствам могут приближаться к идеальным, но для них также используют схемы замещения разных уровней. Они содержат идеальный источник напряжения или тока и пассивные элементы, отражающие внутренние свойства источника – внутреннее сопротивление. Если внутреннее сопротивление источника очень мало, то такой источник близок к идеальному источнику напряжения, если очень велико, то к идеальному источнику тока.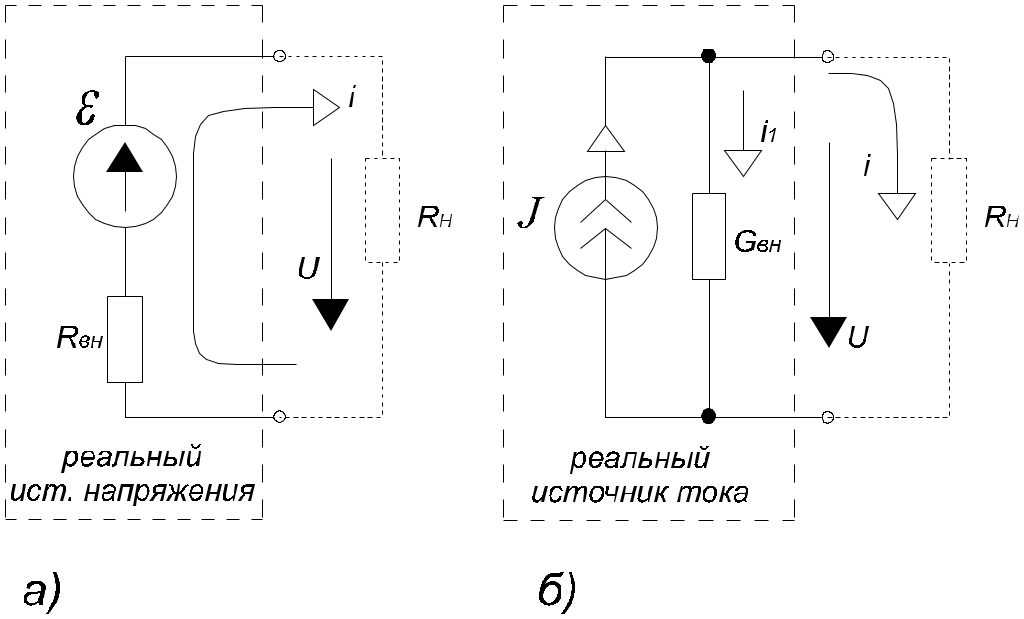


Простейшие схемы замещения источников. R_H – сопротивление нагрузки (потребителя)

Внутреннее сопротивление в модели с источником напряжения (ЭДС) включается последовательно, а с источником тока – параллельно и отражает потери энергии внутри реального источника. При этом ЭДС идеального источника определяется напряжением на разомкнутых зажимах реального источника (U_XX), а ток идеального источника – током через закороченные зажимы реального источника (I_КЗ). Тогда R_ВН = U_XX / I_КЗ . Для внешних токов и напряжений эти схемы замещения эквивалентны, то есть внешние токи и напряжения будут одинаковыми. По внутренним потерям они различаются.. Схема с источником напряжения не дает потерь при холостом ходе (отключенная нагрузка), а с источником тока – при коротком замыкании. Для более полного учета потерь энергии добавляют в схему замещения еще резистивные сопротивления (параллельно в первой схеме и последовательно во второй).Также реальные источники могут обладать свойствами емкостными и индуктивными, что отражают в схемах замещения при уточнении модели источника.

2.5. Основные топологические понятия и параметры ЭЦ

К таким понятиям относят понятия ветви, узла и контура ЭЦ (ЭС).

Под ветвью понимают участок ЭЦ, где протекает один и тот же не разветвляющийся электрический ток. Простейшая ветвь состоит из одного элемента, сложная – из несколь­ких последовательно соединенных элементов. Количество ветвей в цепи является тополо­гическим или структурным параметром N_B . Ветви в расчетной эквивалентной схеме зависят от выбранных схем замещения деталей. В учебных задачах мы будем в основном рассмат­ривать готовые расчетные эквивалентные схемы, а в практической работе может потребо­ваться самому составить расчетную эквивалентную схему.

Узел – это точка соединения трех и более проводников от каких-то элементов цепи.

Точка соединения проводников от двух элементов называется устранимым узлом и обычно не учитывается. Устранимые узлы используются, когда надо детально описать расположение элементов, например, при компьютерных расчетах. На схемах в ряде слу­чаев показывают многоточечные узлы (между точками нет никаких элементов). Такой узел считается за один. Количество узлов является топологическим или структурным параметром цепи N_УЗ.

Под контуром понимают замкнутый путь, проходящий по элементам ЭЦ через ее ветви и узлы. В ряде случаев используют так называемый неявный проход через какие-то эле­менты. Структурным или топологическим параметром цепи является количество незави­симых контуров, где каждый последующий отличается от всех других хотя бы одним эле­ментом, одной ветвью и где все элементы охвачены контурами.

Существует структурная или топологическая формула для определения количества независимых контуров.



Рассмотрим следующий пример: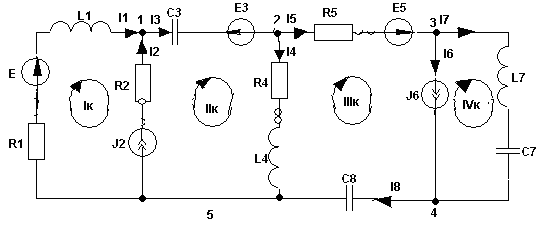


Здесь N_в=8 N_уз=5 5 узел здесь двухточечный. N_нк=8-5+1=4 . Для простых схем число независимых контуров равно количеству различных замкнутых ячеек.

Направление обхода по контуру выбирается произвольно, но указывается на схеме и по­том не меняется.

2.6. Законы Кирхгофа

Первый закон Кирхгофа – это физический закон баланса токов в узле, основан на том, что заряды в узле не накапливаются, а перемещаются по проводникам.

Формулировка: алгебраическая сумма мгновенных значений токов узла равна 0 в любой момент времени. Правило знаков: токи, направленные к узлу, берутся с одним знаком (+), от узла – с про­тивоположным (-). Для примера рассмотри схему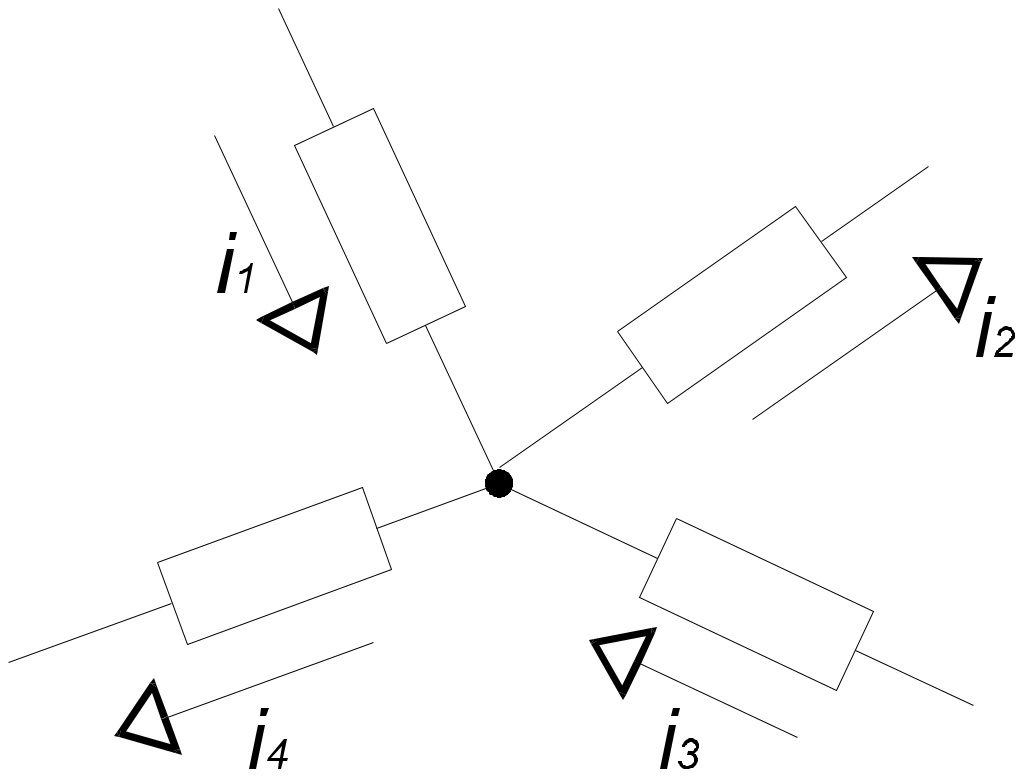

i₁ - i₂ + i₃ - i₄ = 0

Если взять1 узел из схемы предыдущего параграфа то для первого узла в ней

i₁(t) + i₂(t) – i₃(t) = 0

Е 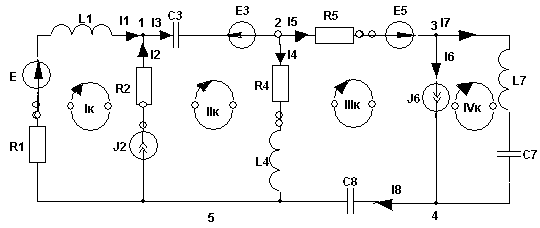сть вторая формулировка: сумма подходящих к узлу токов равна сумме отходящих от узла токов для мгновенных значений.

i₁(t) + i₂(t) = i₃(t) (см. сх.)

Используется та запись, которая удобна в конкретном случае.

Для конкретной схемы можно составить столько уравнений, сколько узлов, но независи­мых уравнений на единицу меньше числа узлов. N_нуIзк=N_уз – 1 ( =4)

Второй закон Кирхгофа – это физический закон баланса напряжений в замкнутом кон­туре.

Формулировка: алгебраическая сумма мгновенных значений напряжений на элементах контура равна 0 в любой момент времени. Правило знаков: напряжения, совпадающие с обходом по контуру, берутся со знаком “+”, не совпадающие – со знаком “-”.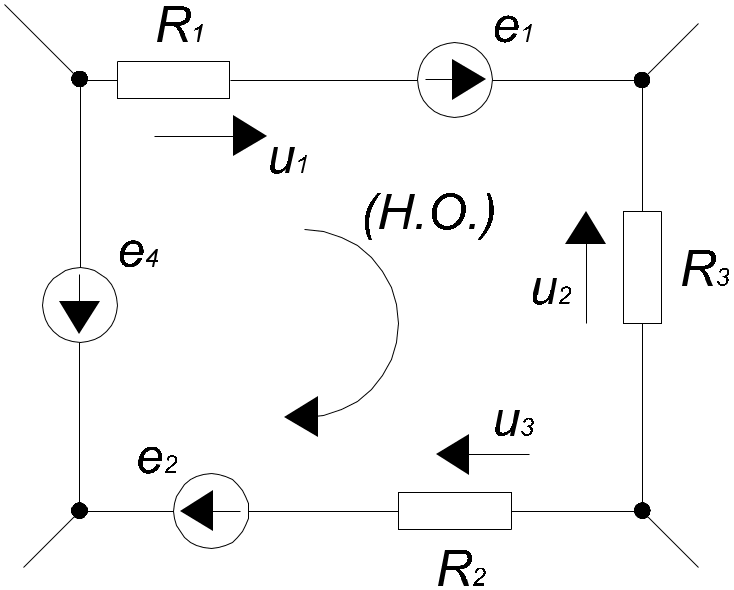

u₁- u_e1 - u₂ + u₃ -u_e2 +u_e4= 0 Напряжение на источнике ЭДС равняется ЭДС и направляется противоположно. Оно является обычно заданной величиной. Поэтому целесообразно такие напряжения переносить в правую часть уравнения. u₁ - u₂ + u₃ = е₁ +е₂-е₄ В результате получается вторая формулировка (рабочая): алгебраическая сумма напряже­ний на элементах контура за исключением источников ЭДС равна алгебраической сумме ЭДС в этом контуре. Все справедливо для мгновенных значений.

Число независимых уравнений по II закону Кирхгофа равно числу независимых контуров. N_нуIIзк=N_нк (=4) Для 1 контура большой схемы можно записать

u_R1 – u_e1 + u_L1 – u_R2 + u_j2 = 0 (напряжение на источнике тока взято противоположного направления относительно источника) . Можно переписать: u_R1 + u_L1 – u_R2 + u_j2 = e₁

В итоге для схемы электрической цепи можно составить целую систему уравнений, коли­чество которых N_нуIIзк + N_нуIзк = N_уз + N_нк – 1 = N_в