ОТЦ. Лекции по ОТЦ Часть 1. Конспект лекций по дисциплине Основы теории цепей (часть I) Составитель к т. н., доц. Михайлов В. И. Самара, 2008 г
 Скачать 3.24 Mb. Скачать 3.24 Mb.
|
5. Электрические цепи с взаимно индуктивнымисвязями и методы их расчета§1. Основные понятия о взаимной индукции При протекании тока через проводник вокруг него появляется магнитное поле, которое оценивается магнитным потоком Ф и в случае обмотки из проводника потокосцеплением Ψ=Ф▪N (N – число проводников или витков с которыми сцеплен магнитный поток).При этом это магнитное поле наводит эдс(напряжение) в проводниках. Когда проводник своим магнитным полем влияет на себя, это называют явлением самоиндукции Под взаимной индукцией понимают явление наведения ЭДС(напряжения) в проводнике под действием магнитного поля, созданного током другого проводника. Условием является изменяющееся магнитное поле. Может быть два варианта: либо меняется ток, либо положение проводников; может быть комбинированно. . 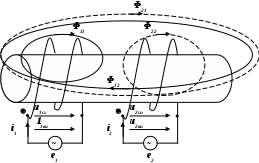 N1 N2 Ф1=Ф11+Ф12 Ф2=Ф22+Ф21 M12 – взаимная индуктивность, отражающая влияние по магнитному полю 1 обмотки на 2. Аналогично второй проводник будет влиять на первый. Ставится знак «+», когда свой и влияющий магнитные потоки совпадают. Такое включение токов (магнитных потоков, обмоток) называют согласным. Если не совпадают, выбирается знак «-». Такое включение обмоток называют встречным. Тип включения обмоток несколько условен, поскольку зависит от выбранного положительного направления тока. Обычно M12=M21 в изотропной среде по магнитным свойствам. Но в принципе бывают магнитно-анизотропные среды, тогда данное равенство не выполняется. Может быть и третья, и четвертая обмотки. Можно ли избавиться от магнитного влияния? да, если токи постоянные и проводники неподвижны. можно за экранировать проводники. можно разместить проводники перпендикулярно. При расчете электрических цепей изображают схему замещения цепи, где направление обмоток и расположение их в пространстве конкретно не показывают и определить тип включения невозможно. В связи с этим вводят специальное понятие одноименных или однополярных зажимов индуктивно связанных элементов, которые специальным знаком указываются на схемах. например точкой. Если выбрать токи, одинаково протекающие относительно одноименных зажимов, то тип включения будет согласным. На примере одноименные зажимы показаны точками. Расчет взаимной индуктивности – довольно сложная задача, обычно ей занимаются в электротехнике. Для этого используют понятие коэффициента связи. 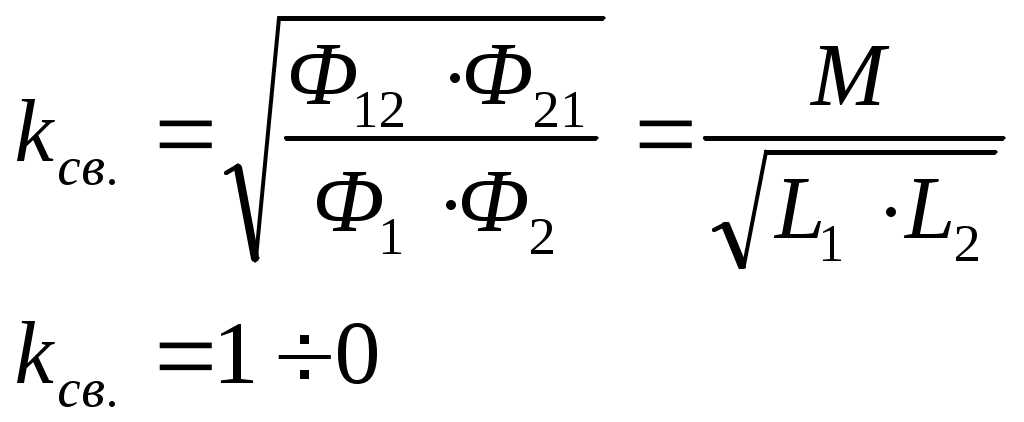 §2. Последовательное и параллельное соединения индуктивно связанных элементов 1. Последовательное соединение Изобразим схему замещения последовательно магнитно связанных элементов. Здесь может быть 2 варианта расположения одноименных зажимов – согласное (одноименные зажимы с одной стороны обмоток) и встречное ( с разных сторон). 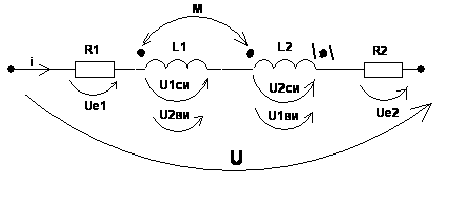 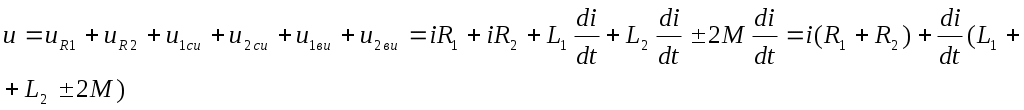 2. Параллельное соединение Изобразим схему замещения параллельно соединенных элементов. 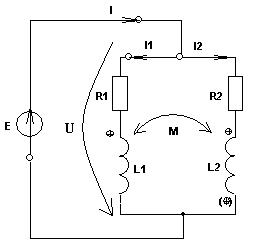 Будем рассматривать действие гармонической ЭДС. Соответственно все уравнения можно записывать в комплексной форме. Составим уравнения: одно по первому закону Кирхгофа и два – по второму с учетом влияния взаимной индукции (в комплексной форме). 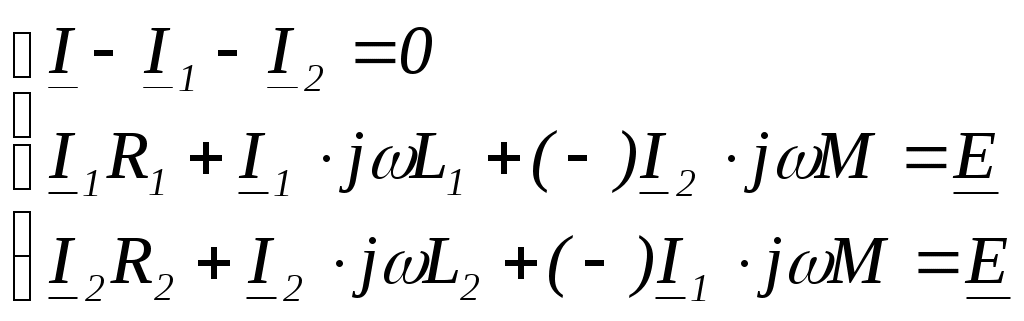 Математически решая, можно получить токи. Результат расчетов при согласном и встречном включениях различен. Он зависит от положения одноименного зажима. §3. Электрический трансформатор Электрический трансформатор – это устройство, которое трансформирует (преобразует) электрическое напряжение, ток или сопротивление с помощью явления взаимной индукции. ЭТ содержит двое или более индуктивно-связанных обмоток, может иметь сердечник из магнитного или немагнитного материала. 1. Идеальный трансформатор n 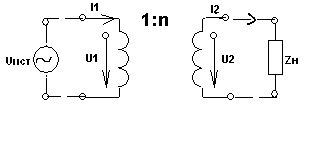 – коэффициент трансформации – коэффициент трансформацииДля идеального трансформатора всегда выполняется условие: Говорят, что трансформатор трансформирует напряжение в n раз, а ток в 1/n. Мощность не меняется: на входе и на выходе она одинакова 2. Уравнения и схемы замещения реального трансформатора (двухобмоточного, без ферромагнитного сердечника) 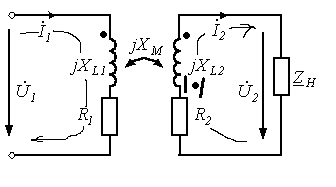 Уравнения составляются по второму закону Кирхгофа: 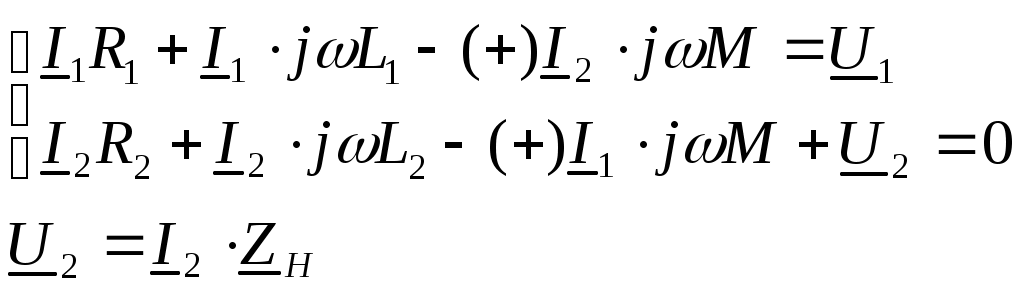 Знак в скобках соответствует нижнему положению второго одноименного зажима. Рассмотрим различные режимы работы ЭТ: 1) 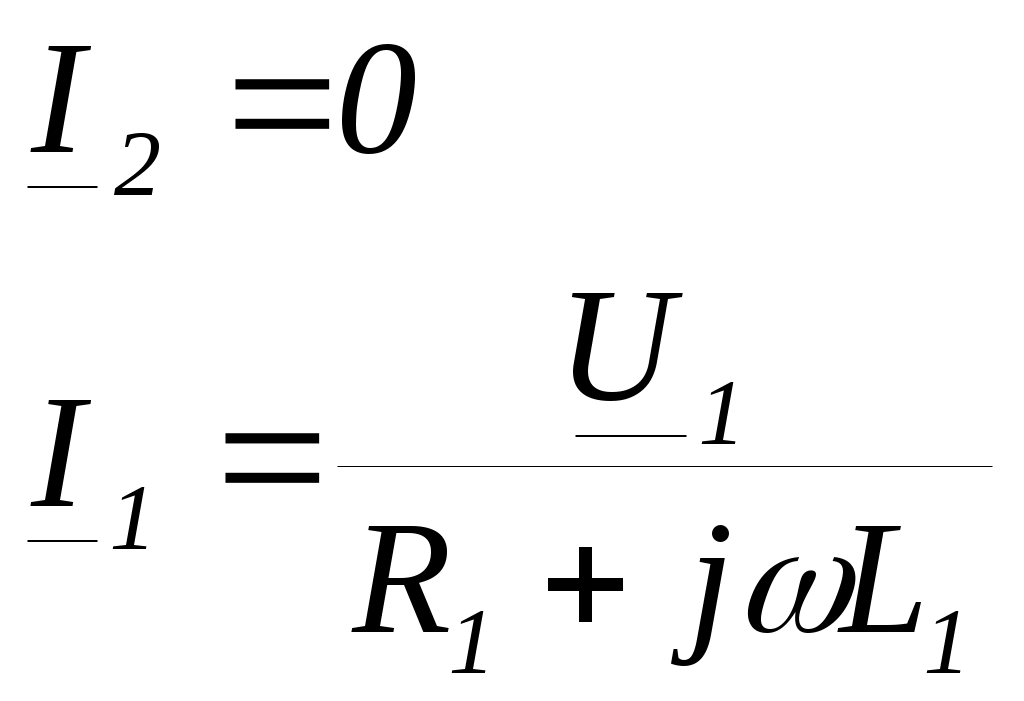 Если хороший трансформатор, то 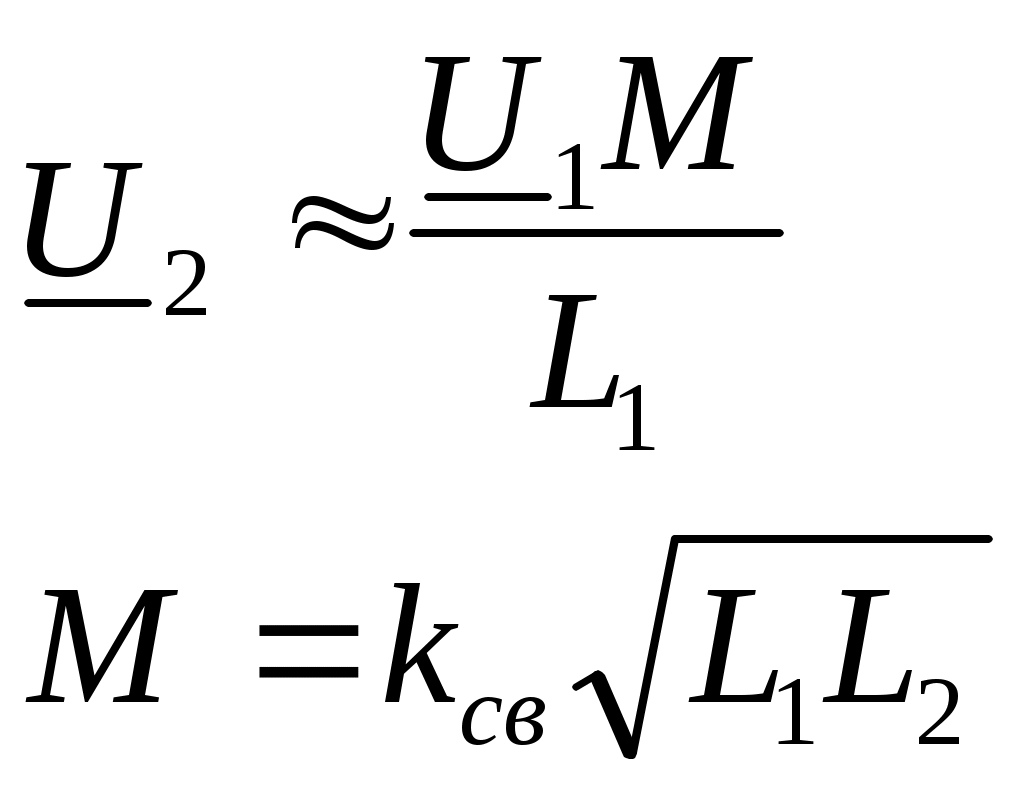 У трансформатора близкого к идеальному kсв=1. У трансформатора близкого к идеальному kсв=1.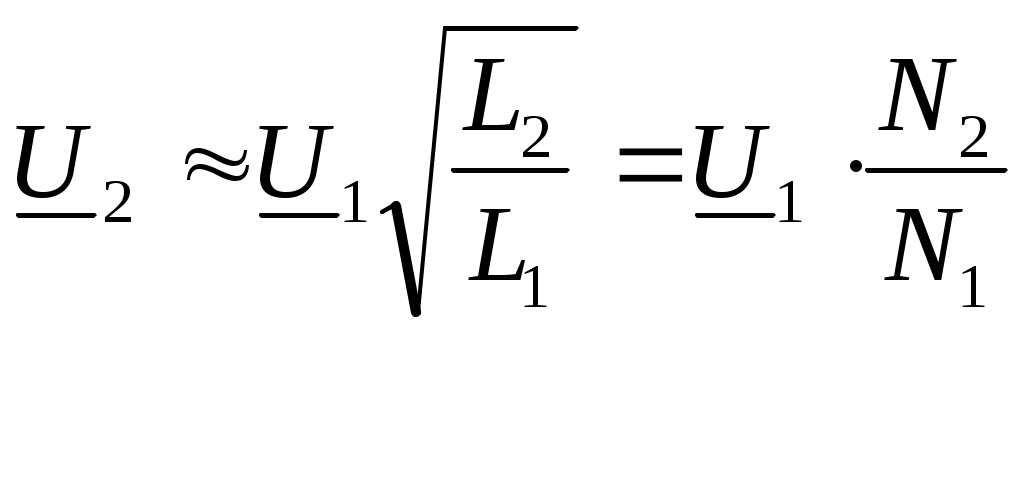 Величина индуктивностей пропорциональны квадрату числа витков обмоток. Величина индуктивностей пропорциональны квадрату числа витков обмоток. 2) По принципу дуальности Технически различают трансформаторы напряжения (они хорошо трансформируют напряжение, N – большое, Чаще используются трансформаторы напряжения. Есть еще трансформаторы сопротивления (N – среднее, используются для согласования сопротивления нагрузки и сопротивления источника сигнала) 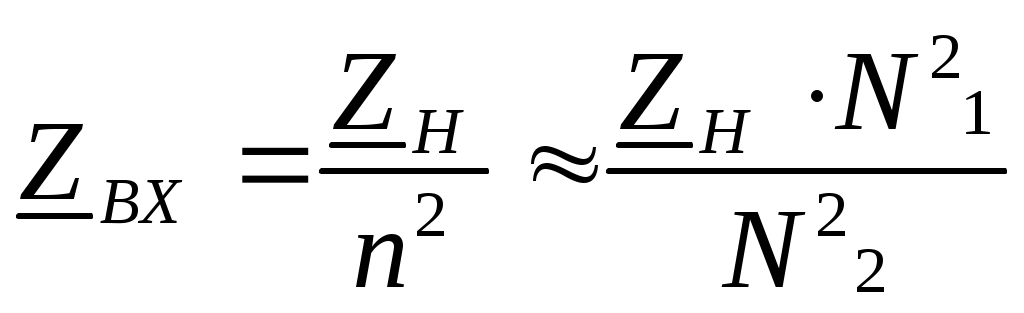 . .3. Входное сопротивление реального трансформатора 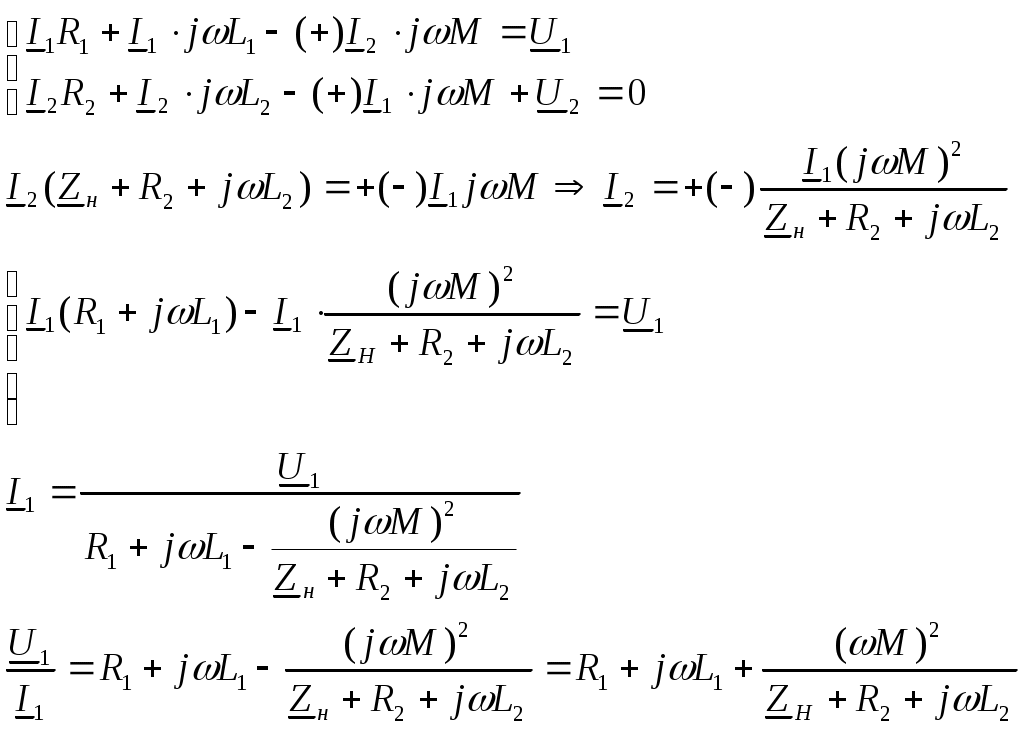 §4. Развязка индуктивных (магнитных связей) Р 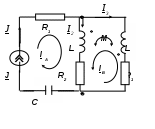 ассмотрим схемы с магнитными связями. ассмотрим схемы с магнитными связями.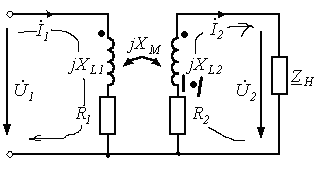 Составление Т-обратной схемы Это эквивалентная схема, в которой получаются те же уравнения, что и в схеме с магнитной связью (между L1 и L2). Такая замена возможна только если индуктивности соединены проводником. Нижний конец буквы Т направляется в место соединения магнитно связанных индуктивностей Когда есть магнитная связь, нельзя применять МУН. Поэтому делают развязку магнитных связей. 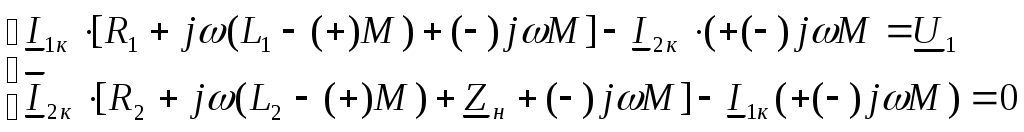 У 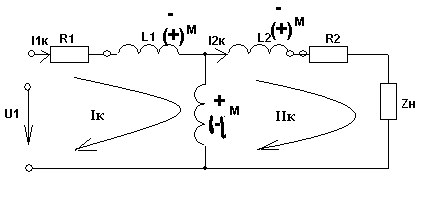 равнения по МКТ должны быть в схемах одинаковыми. Знак без скобок выбирается при соединение вместе одинаковых (одноименных) зажимов L1 и L2 и в скобках при не одноименных.. равнения по МКТ должны быть в схемах одинаковыми. Знак без скобок выбирается при соединение вместе одинаковых (одноименных) зажимов L1 и L2 и в скобках при не одноименных..2. Развязка с использованием зависимых источников 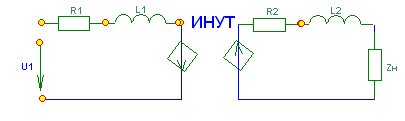 §5. Автотрансформатор 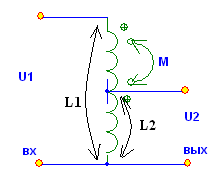 Автотрансформатор – трансформатор, у которого вторичная обмотка является частью первичной обмотки, с целью экономии провода. Здесь вместе соединены разноименные зажимы. §6. Общие методы расчета цепей с взаимными индуктивными элементами Используют метод токов ветвей Используют метод контурных токов, хотя иногда возникают трудности, с учетом взаимного влияния по магнитному полю Метод узловых напряжений применять нельзя, можно только после развязки индуктивных связей 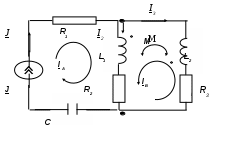 Число уравнений 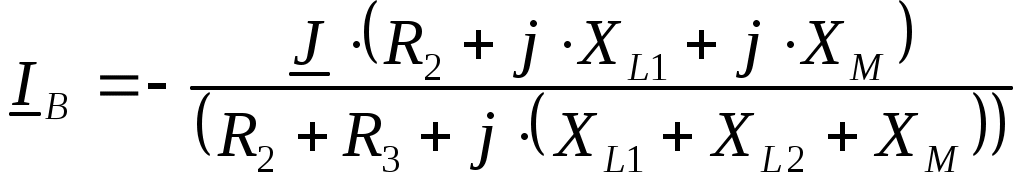 Через контурный ток |
