Арифметическая прогрессия алгебра. Конспект открытого урока по математике
 Скачать 184.31 Kb. Скачать 184.31 Kb.
|
|
КОНСПЕКТ ОТКРЫТОГО УРОКА ПО МАТЕМАТИКЕ Современный урок трудно представить без использования информационно-коммуникационных технологий. Использование электронных образовательных ресурсов (ЭОР) значительно облегчает и сокращает время подготовки учителя к уроку. ЭОРы развивают активно-деятельностные формы обучения; способствуют осознанию учащимися процесса обучения; развивают познавательную активность учащихся; способствуют достижению наивысшего возможного результата в общем развитии всех учеников, в том числе самых сильных и самых слабых; позволяют провести рефлексию знаний. Более того, дают возможность «конструировать» школьные уроки и другие учебные занятия, определяя их оптимальное содержание, формы и методики обучения; способствует организации учебного процесса. Задания, которые я использовала на уроке, дают возможность повторить и закрепить пройденный материал, подготовить учащихся к контрольной работе. ПЛАН - КОНСПЕКТ УРОКА ФИО: Кузьменко Наталья Николаевна Место работы: ГБОУ гимназия г.Сызрани Должность: учитель математики Предмет: алгебра Класс: 9 Тема и номер урока в теме: «Арифметическая прогрессия», урок 1. Базовый учебник: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова «Алгебра-9» Цель урока: сформировать понятие арифметической прогрессии и ее компонентов; научить применять полученные знания при решении основных типов задач на арифметическую прогрессию. Образовательная цель (формирование познавательных и логических УУД): формирование первоначальных представлений об арифметической прогрессии; поиск и выделение необходимой информации; подведение под понятия; выведение следствий; устанавливать причинно – следственные связи; строить логическое рассуждение и делать выводы; формирование образовательной компетентности. Развивающая цель: (формирование регулятивных УУД) умение определять понятия, создавать обобщения; развитие умений анализировать. Воспитательная цель (формирование личностных УУД) воспитание настойчивости в достижении цели и заинтересованности в конечном результате труда; умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблемы, доказывать свою точку зрения; формирование целостного мировоззрения. Задачи: Обеспечить осознание и усвоение понятия арифметической прогрессии и ее компонентов; Формирование УУД при решении задач и формировании новых знаний; Способствовать индивидуализации и дифференциации обучения с помощью информационно-коммуникационных технологий. Тип урока: объяснение нового материала Формы работы учащихся: индивидуальная и фронтальная работа Оборудование: компьютер (выход в интернет), экран, доска, документ камера, акустическая система, мультимедийный проектор, раздаточный материал Длительность: 1 урок Структура и ход урока Методическая литература и ЭОР А.Г.Мордкович «Алгебра 9», учебник, «Мнемозина», 2010 А.Г.Мордкович «Алгебра 9», задачник, «Мнемозина», 2010 Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова «Алгебра-9» 2009 Л.А.Александрова, «Самостоятельные работы. Алгебра 9», «Мнемозина», 2010 Лебединцева Е.А., Беленкова Е.Ю. Алгебра 9 класс. Задачи для обучения и развития учащихся. – М.: Интеллект-Центр, 2006. Энциклопедия для детей. – М., Аванта +, 1997. Лиман М.М.Школьникам о математике и математиках. – М., Просвещение, 1981. http://ru.wikipedia.org http://fcior.edu.ru/card/1997/opredelenie-arifmeticheskoy-progressii-svoystvo http://math.oge.sdamgia.ru/test?theme=9 http://www.bryanskedu.net/metodik/math/didakt/ Ход урока. Орг.момент, приветствие, пожелания. Здравствуйте, ребята!. Садитесь, пожалуйста. Сегодняшний урок я хотела бы начать словами: Закончился 20-ый век. Куда стремится человек? Изучены и космос, и моря, Строенье звёзд и вся Земля. Но математиков зовёт Известный лозунг: «Прогрессио - движение вперёд». Я хочу, чтобы наша встреча сегодня принесла много открытий, опыта и хорошего настроения. Вместе с вами мы будем двигаться только вперёд, т.к. слово «Прогрессио» в переводе с греческого языка означает движение вперёд. Немного истории С  ведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. На связь функции с прогрессией обратил внимание Архимед еще во времена до нашей эры. ведения, связанные с прогрессиями, впервые встречаются в дошедших до нас документах Древней Греции. На связь функции с прогрессией обратил внимание Архимед еще во времена до нашей эры.Актуализация знаний учащихся. Ребята, предыдущие уроки алгебры были посвящены теме «Последовательности». Для того чтобы перейти к изучению понятия прогрессия, необходимо вспомнить некоторые понятия: - Какая последовательность называется числовой? - (Числовая последовательность - это функция, заданная на множестве натуральных чисел) - Какие способы задания последовательностей вы знаете? - (аналитический, рекуррентный, словесный) -Что значит, последовательность задана аналитически? -(Последовательность задана аналитически, если указана формула его n – ого члена уn = f(n) - Что значит, последовательность задана рекуррентно? - (Задается формула, по которой каждый следующий член находят через предыдущие члены. В случае рекуррентного способа задания функции всегда дополнительно задается один или несколько первых членов последовательности.) - Задайте последовательность словестным способом -(Последовательность всех неотрицательных чисел, кратных числу 5. 0; 5; 10; 15; 20; 25; ...) 4. Объяснение нового материала. Рассмотрим с вами последовательности: 2; 6; 10; 14; 18; 22; 26….. 10 124 -6 45 76 -12 90 876 … - Что записано на слайде? - (числовые последовательности) - Действительно ребята числовые последовательности, как мы с вами выяснили и этот ряд чисел бесконечный, чтобы перечислить нам не хватит жизни. Поэтому числовые последовательности задают формулами. - Какую особенность в записи данных последовательностей вы увидели? -(1-я члены последовательности записаны в порядке возрастания, и каждый последующий член отличается от предыдущего ровно на 4; - а как вы посчитали что на 4? -(6-2=4; 10-6=4) - Данная последовательность называется арифметической прогрессией. Она является частным случаем числовой последовательности. Обозначают 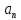 , где а – это член последовательности, а n- его номер в ряду чисел.. , где а – это член последовательности, а n- его номер в ряду чисел..Рассмотрим еще пример на слайде - Если мы к первому члену данной последовательности «3» прибавим «4», то получим второй член последовательности «7», если к нему мы прибавим еще «4» то получим «11» и т.д. мы можем получить таким образом любой член последовательности. - А что означает число 4? Число 4- это разность арифметической прогрессии, она обозначается буквой d. - Приведите пример арифметической прогрессии Теперь перейдем к общим рассуждениям. Но это мы рассмотрели на примере, а если нам рассмотреть в общем виде: Пусть нам задана числовая последовательность в которой: а1- первый член последовательности, а2- второй…. аn—ый член последовательности буквой d- обозначим разность между последующим и предыдущем членом данной последовательности. Сможем ли мы с вами сказать какая же последовательность может называться арифметической прогрессией ? Попытайтесь своими словами объяснить, что такое арифметическая прогрессия - (Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.) На примере мы с вами рассмотрели как можно задать следующий член последовательности, зная первый член прогрессии и разность между последующим и предыдущим членом, а как найти любой n – ый член прогрессии. Например тысячный, миллионный….Попробуйте. Пусть задана арифметическая прогрессия: 3;9;15…. Нужно найти  . .Сможем мы сразу это сделать, или придется подставлять и считать. - (это не рационально требует много времени) - Да, ребята если мы будем считать, последовательно суммируя разность арифметической прогрессии и предыдущий член последовательности, чтобы узнать миллионный член данной прогрессии то нам потребуется, достаточно много времени. - Но это можно сделать быстро. Для этого мы с вами выведем формулу! Путь задана арифметическая прогрессия 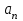 , с первым членом , с первым членом 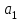 и разностью d, тогда и разностью d, тогда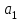 = =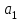 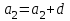 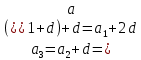 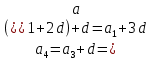 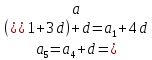 ….. …..- Какую закономерность увидели? ( что каждый последующий член - это а1 член плюс произведение разности последующего члена и предыдущего на число меньшего на единицу чем порядковый номер члена прогрессии) Итак формула как же будет записан n-ый член прогрессии? 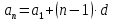 , где n-номер члена, , где n-номер члена, 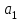 – первый член, d - разность арифметической прогрессии , аn –n-ый член этой прогрессии – первый член, d - разность арифметической прогрессии , аn –n-ый член этой прогрессии- Вернемся к нашей задаче, попробуем ее решить, применяя эту формулу. Пусть задана арифметическая прогрессия: 3;9;15…. Нужно найти  . .- 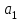 =3, d=9-3=6 =3, d=9-3=6  = 3+(1000000-1)6=3+999999*6=3+5999994=5999997 = 3+(1000000-1)6=3+999999*6=3+5999994=5999997Молодцы! Работа с текстом. У Вас на столах есть распечатки текстов о арифметической прогрессии, Ваша задача прочитать этот текст и найти тот теоретический материал, который мы с вами еще не рассмотрели и назвать мне его и запишите его в свои тетради. Арифметические прогрессии подразделяются по способу задания: Возрастающей, если в арифметической прогрессии разность d > 0. Убывающей, если в арифметической прогрессии разность d <0. Постоянной, если в арифметической прогрессии d = 0. 5. Решение задач (закрепление изученного материала) - Итак, теоретический материал рассмотрели, перейдем к практике. Вам в этом году проходить Государственную Итоговую аттестацию , и задачи связанные с арифметической прогрессией встречаются в материалах подготовки к экзамену это задание №6. Поэтому при изучении данной темы нам необходимо рассмотреть все типы задач на арифметическую прогрессию. Сегодня мы с вами рассмотрим некоторые типы задач, которые могут Вам встретится на ОГЭ. Для этого мы переместимся на известный нам сайт Дмитрия Гущина. Все решения выполняют учащиеся около доски с полным пояснением под руководством учителя Задание 6 № 321663. Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x . Решение. Найдем разность арифметической прогрессии: Ответ: −11. Задание 6 № 339063. Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9. Решение. Член арифметической прогрессии с номером Ответ: 28,7. Задание 6 № 113. Дана арифметическая прогрессия Решение. Определим разность арифметической прогрессии: Член арифметической прогрессии с номером Необходимо найти Ответ: 23. 20 Задание 6 № 321384. В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду? Решение. Число мест в ряду представляет собой арифметическую прогрессию с первым членом Необходимо найти Ответ: 38. 3 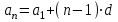 )Дана арифметическая прогрессия 1,3,5,7…. Составим формулу n-го члена. )Дана арифметическая прогрессия 1,3,5,7…. Составим формулу n-го члена.Прежде чем составлять формулу для данной прогрессии запишем общую: a1 =1 разность соседних членов арифметической прогрессии d=5-3=2 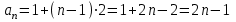 Подставим в формулу: (чему равен первый член прогрессии и разность членов прогрессии мы составили формулу для вычисления n-го члена прогрессии) Подставим в формулу: (чему равен первый член прогрессии и разность членов прогрессии мы составили формулу для вычисления n-го члена прогрессии)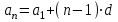 4) Дана арифметическая прогрессия: 4) Дана арифметическая прогрессия: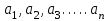 . Известно, что а5=6, d=2Найти а1 . Известно, что а5=6, d=2Найти а1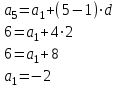 6. Самостоятельная работа (в парах) Всем учащимся даются задачи практического содержания. Кто быстрее решит предоставляет свое решение на документ камеру и объясняет ход решения Задача №1 Для участия в международной математической игре «Кенгуру – математика для всех» в оргкомитет необходимо подать заявку от школы. В первый день после указанного срока подали заявки 5 школ, во второй день 7 школ, а в третий 9 школ. Считая, что закономерность не будет нарушена, вычислите сколько заявок будет подано на 7-й день. 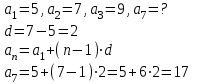 17 заявок будет подано на 7-й день 17 заявок будет подано на 7-й деньзадача №2 В январе в городе произошло 60 автомобильных аварий. Благодаря мерам, предпринимаемым дорожными службами, в каждый следующий месяц число аварий становилось на 4 меньше. Сколько предположительно ожидается ДТП в 6 месяце? 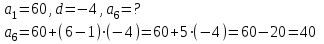 ожидается дтп в 6 месяце.. ожидается дтп в 6 месяце..задача №3 Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Сколько они отложат в 10 месяц? 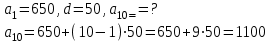 рублей отложат родители рублей отложат родители7. Рефлексия, подведение итогов У Вас на партах лежит листок, на котором напечатаны не оконченные предложения, прошу выбрать любой и закончить его 1. Сегодня я узнал… 2. Было интересно… 3. Было трудно… 4. Я выполнял задания… 5. Я понял, что… 6. Теперь я могу… 7. Я почувствовал, что… 8. Я приобрел… 9. Я научился… 10. У меня получилось… 11. Я смог… 12. Я попробую… 13. Меня удивило 14. Мне захотелось… - Итак, ребята мы сегодня с Вами познакомились с арифметической прогрессией . что это за прогрессия? Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом - 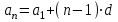 Запишите формулу для отыскания n-го члена прогрессии Запишите формулу для отыскания n-го члена прогрессииМы, потрудились с Вами на славу, я думаю, что этот урок поможет Вам на выпускных экзаменах. А закончить урок я хотела бы словами: "Прогрессио – движение вперёд!" Урок сегодня завершён, Но каждый должен знать: Познание, упорство, труд Всегда к прогрессу в жизни приведут. Структура и ход урока
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом. 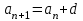 Разностью арифметической прогрессии называется число, показывающее на сколько каждый последующий член больше или меньше предыдущего. Обозначают буквой d. Формула n-ого члена арифметической прогрессии имеет вид: 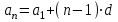 Арифметические прогрессии подразделяются по способу задания: Возрастающей, если в арифметической прогрессии разность d > 0. Убывающей, если в арифметической прогрессии разность d <0. Постоянной, если в арифметической прогрессии d = 0. Обязательно запишите к себе в тетрадь: - формулу, определяющую арифметическую прогрессию; - формулу n-ого члена арифметической прогрессии; - способы задания арифметической прогрессии. Задачи, решаемые на уроке Задание 6 № 321663. Выписано несколько последовательных членов арифметической прогрессии: …; −9; x; −13; −15; … Найдите член прогрессии, обозначенный буквой x.Решение. Определим разность арифметической прогрессии: Член арифметической прогрессии с номером Необходимо найти Ответ: 23. Ответ: 23 Задание 6 № 339063. Дана арифметическая прогрессия (an), разность которой равна 2,5, a1 = 8,7. Найдите a9. Задание 6 № 113. Дана арифметическая прогрессия Задание 6 № 321384. В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду? Задание 6 Дана арифметическая прогрессия 1,3,5,7…. Составим формулу n-го члена. Задачи, решаемые в парах на уроке 1 задача:Для участия в международной математической игре «Кенгуру – математика для всех» в оргкомитет необходимо подать заявку от школы. В первый день после указанного срока подали заявки 5 школ, во второй день 7 школ, а в третий 9 школ. Считая, что закономерность не будет нарушена, вычислите сколько заявок будет подано на 7-й день. 2 задача: В январе в городе произошло 60 автомобильных аварий. Благодаря мерам, предпринимаемым дорожными службами, в каждый следующий месяц число аварий становилось на 4 меньше. Сколько предположительно ожидается ДТП в 6 месяце? 3 задача: Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Сколько они отложат в 10 месяц? Выберите любое понравившееся предложение и закончите его: 1. Сегодня я узнал… 2. Было интересно… 3. Было трудно… 4. Я выполнял задания… 5. Я понял, что… 6. Теперь я могу… 7. Я почувствовал, что… 8. Я приобрел… 9. Я научился… 10. У меня получилось… 11. Я смог… 12. Я попробую… 13. Меня удивило 14. Мне захотелось… | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
