Контрольная 1, вариант 3 Задание Введите переменные
 Скачать 147.28 Kb. Скачать 147.28 Kb.
|
|
Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 1-ая строка, а переменную x4 следует вывести из базиса. Минимальное значение θ соответствует 1-му столбцу, т.е. переменную x1 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-400).
Выполняем преобразования симплексной таблицы
В базисном столбце все элементы положительные. Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 6, x2 = 0, x3 = 0 F(X) = 200•6 + 200•0 + 300•0 = 1200 Задание 5. Решить задачу линейного программирования симплексным методом с введением искусственного базиса. Найти максимальное значение функции  Z(X)=с1+с2+с3 при условных: Z(X)=с1+с2+с3 при условных:  х х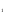 , х , х , х , х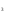 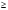 0 (см. табл. 11) 0 (см. табл. 11) Решение Определим максимальное значение целевой функции F(X) = 3x1-x2 при следующих условиях-ограничений. 3x1+x2≤30 x1-x2≥10 x3≤70 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 3x1+x2+x4 = 30 x1-x2-x5 = 10 x3+x6 = 70 Расширенная матрица системы ограничений-равенств данной задачи:
Приведем систему к единичной матрице Получаем новую матрицу:
3. В качестве базовой переменной можно выбрать x6. Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,5,6). Выразим базисные переменные через остальные: x4 = -3x1-x2+30 x5 = x1-x2-10 x6 = -x3+70 Подставим их в целевую функцию: F(X) = 3x1-x2 Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным. Вместо переменной x5 следует ввести переменную x1. Выполняем преобразования симплексной таблицы
Представим расчет каждого элемента в виде таблицы:
Выразим базисные переменные через остальные: x4 = -4x2-3x5 x1 = x2+x5+10 x6 = -x3+70 Подставим их в целевую функцию: F(X) = 3(x2+x5+10)-x2 Или F(X) = 2x2+3x5+30 4x2+x4+3x5=0 x1-x2-x5=10 x3+x6=70 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Решим систему уравнений относительно базисных переменных: x4, x1, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (10,0,0,0,0,70)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
