Контрольная 1, вариант 3 Задание Введите переменные
 Скачать 147.28 Kb.
|
|
Задание №7. Предприятие выпускает 2 вида продукции. Обозначения норм расхода сырья и прибыли от единицы продукции указаны в табл. 12. Численные данные по вариантам приведены в табл. 13., дополнительные ограничения даны в табл. 14. Кроме ограничений на сырье имеются статистически обоснованные ограничения на спрос х1 и х2. Таблица 12
Выполните следующие задания: 1. В соответствии с порядковым номером полученного вами варианта задания, по первым двум столбцам табл. 13 определите римскую цифру (от до VIII) Вашего варианта дополнительных ограничений и арабскую цифру (от 1 до 3) Вашего подварианта числовых данных в табл. 14. 2.Составьте математическую модель задачи: 1) введите переменные, 2) определите целевую функцию, 3) запишите ограничения на сырье, 4) выпишите дополнительные ограничения на спрос, 5) запишите целиком, полученную модель задачи ЛП, 6) подставьте числовые данные Вашего варианта. 3. Решите полученную задачу ЛП графически или симплекс-методом. 4. Составьте двойственную задачу ЛП. 5. Определите двойственные оценки по теореме двойственности. Сравните с индексной строкой последней симплекс-таблицы. 6. Выпишите матрицу устойчивости. Найдите интервалы устойчивости двойственных оценок при изменении каждого сырья в отдельности. Решение
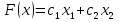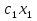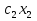1) Обозначим через х1,х2 выпускаемую единицу продукции. 2) Целевая функция :  где  – прибыль от продукции № 1; – прибыль от продукции №2;3) модель задачи 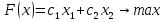 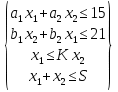 4) 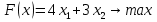 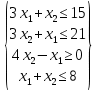 При этом х1,х2 ≥0 5) Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных 3x1+x2+x3 = 15 x1+3x2+x4 = 21 -x1+4x2-x5 = 0 x1+2x2+x6 = 8 Расширенная матрица системы ограничений-равенств данной задачи:
Приведем систему к единичной матрице Получаем новую матрицу:
В качестве базовой переменной можно выбрать x6. Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (3,4,5,6). Выразим базисные переменные через остальные: x3 = -3x1-x2+15 x4 = -x1-3x2+21 x5 = -x1+4x2 x6 = -x1-2x2+8 Подставим их в целевую функцию: F(X) = 4x1+3x2 3x1+x2+x3=15 x1+3x2+x4=21 x1-4x2+x5=0 x1+2x2+x6=8 Решим систему уравнений относительно базисных переменных: x3, x4, x5, x6 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,15,21,0,8)
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x1. Получаем новую симплекс-таблицу:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||