Контрольная 1, вариант 3 Задание Введите переменные

• Название: Контрольная 1, вариант 3 Задание Введите переменные
• Дата: 13.02.2018
• Размер: 147.28 Kb.
• Имя файла: Kontrolnaya_1.docx
• Тип: Решение; #36389
• страница: 6 из 7

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₂, так как это наибольший коэффициент по модулю.

Вычислим значения D_i по строкам как частное от деления: b_i / a_i2

и из них выберем наименьшее:

min (15 : 13 , 21 : 7 , - , 8 : 6 ) = 1²/₁₃

Следовательно, 1-ая строка является ведущей.

Разрешающий элемент равен (13)

Базис	B	x1	x2	x3	x4	x5	x6	min
x3	15	0	13	1	0	-3	0	12/13
x4	21	0	7	0	1	-1	0	3
x1	0	1	-4	0	0	1	0	-
x6	8	0	6	0	0	-1	1	4/3
F(X2)	0	0	-19	0	0	4	0	0

Формируем следующую часть симплексной таблицы. Вместо переменной x₃ в план 2 войдет переменная x₂.

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2	15/13	0	1	1/13	0	-3/13	0
x4	168/13	0	0	-7/13	1	8/13	0
x1	60/13	1	0	4/13	0	1/13	0
x6	14/13	0	0	-6/13	0	5/13	1
F(X2)	285/13	0	0	19/13	0	-5/13	0

Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.

В качестве ведущего выберем столбец, соответствующий переменной x₅.

Разрешающий элемент равен (⁵/₁₃)

Базис	B	x1	x2	x3	x4	x5	x6	min
x2	15/13	0	1	1/13	0	-3/13	0	-
x4	168/13	0	0	-7/13	1	8/13	0	21
x1	60/13	1	0	4/13	0	1/13	0	60
x6	14/13	0	0	-6/13	0	5/13	1	24/5
F(X3)	285/13	0	0	19/13	0	-5/13	0	0

Формируем следующую часть симплексной таблицы. Вместо переменной x₆ в план 3 войдет переменная x₅.

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2	9/5	0	1	-1/5	0	0	3/5
x4	56/5	0	0	1/5	1	0	-8/5
x1	22/5	1	0	2/5	0	0	-1/5
x5	14/5	0	0	-6/5	0	1	13/5
F(X3)	23	0	0	1	0	0	1

Индексная строка не содержит отрицательных элементов - найден оптимальный план

Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6
x2	9/5	0	1	-1/5	0	0	3/5
x4	56/5	0	0	1/5	1	0	-8/5
x1	22/5	1	0	2/5	0	0	-1/5
x5	14/5	0	0	-6/5	0	1	13/5
F(X4)	23	0	0	1	0	0	1

Оптимальный план можно записать так:

x₁ = 4²/₅, x₂ = 1⁴/₅

F(X) = 4•4²/₅ + 3•1⁴/₅ = 23

6) приведение к виду двойственной задачи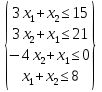



Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется.

Расширенная матрица A.

3	1	15
1	3	21
1	-4	0
1	1	8
4	3

Транспонированная матрица A^T.

3	1	1	1	4
1	3	-4	1	3
15	21	0	8