Контрольная 1, вариант 3 Задание Введите переменные
 Скачать 147.28 Kb. Скачать 147.28 Kb.
|
                 Контрольная 1, вариант 3 Контрольная 1, вариант 3Задание 1. 1. Введите переменные 2. Определить целевую функцию 3. Составить систему ограничений 4. Определить вид математической модели задачи. Диетолог разрабатывает новую диету, состоящую из сливочного масла, натуральных бифштексов (мяса), хлеба и яблочного сока. Содержание калорий, белков, жиров, углеводов и холестерина (в 100 г продукта), а также максимальные и минимальные нормы их потребления (в день) приведены в табл. 2. Здесь же указана цена 100 г соответствующего продукта в рублях. Решение Таблица 2
1) Обозначим через х1,х2 ,х3,х4,количество единиц корма, необходимых к потреблению. 2) Целевая функция : 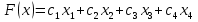 где 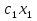 – стоимость масла; – стоимость масла;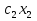 – стоимость мяса; – стоимость мяса;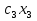 – стоимость хлеба; – стоимость хлеба;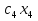 – стоимость сока. – стоимость сока.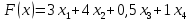 3) Система ограничений: 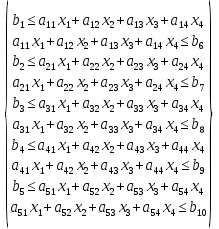 Итого:  При этом х1,х2 ,х3,х4≥0 4) Математическая модель планирования рациона Задание 2. 1. Составить математическую модель задачи линейного программирования. 2. Найти графическое линейное решение задачи. Цех выпускает два вида смесей из цемента и песка. Процентное содержание цемента и песка в смесях, прибыль от продажи 1 т смеси, запасы цемента и песка и максимальное потребление каждой смеси даны в таблице. Таблица 8
Решение 1) Обозначим через х1,х2 количество смеси, необходимой к выпуску. 2) Целевая функция : 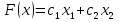 где 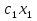 – прибыль от смеси 1; – прибыль от смеси 1;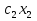 – прибыль от смеси 2; – прибыль от смеси 2;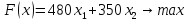 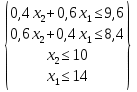 При этом х1,х2 ≥0 Решение Необходимо найти максимальное значение целевой функции F = 480x1+350x2→ max, при системе ограничений: 0,6x1+0,4x2≤9,6 0,4x1+0,6x2≤8,4 x2≤10 x1≤14 x1 ≥ 0 x2 ≥ 0 Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). 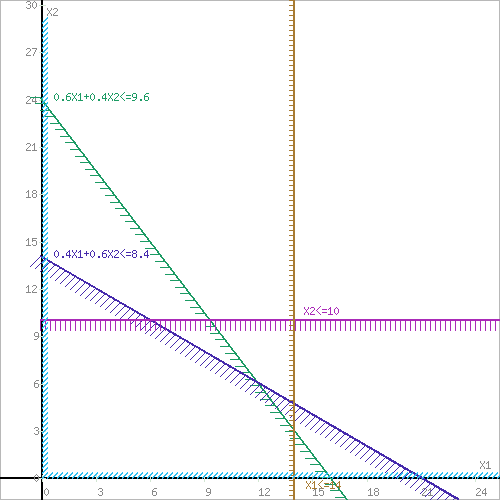 или 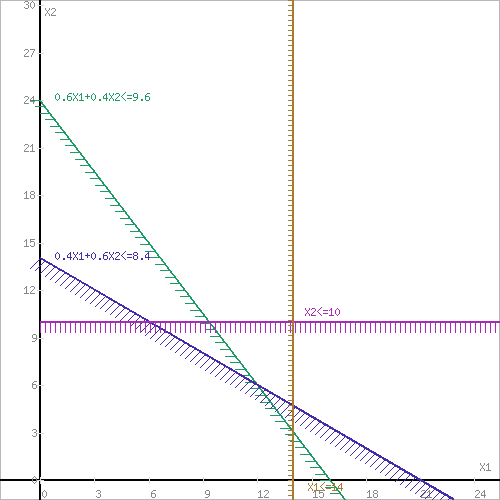 Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 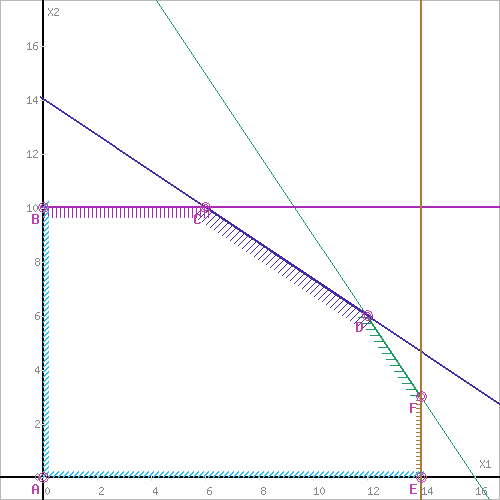 Рассмотрим целевую функцию задачи F = 480x1+350x2 → max. Построим прямую F = 480x1+350x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (480;350). Нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 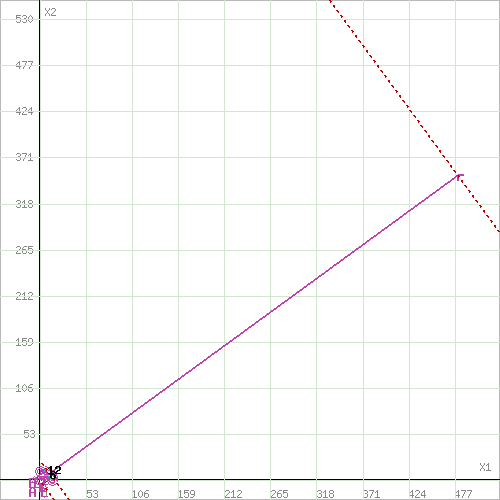 Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых первых двух ограничений, то ее координаты удовлетворяют уравнениям этих прямых: 0.6x1+0.4x2=9.6 0.4x1+0.6x2=8.4 Решив систему уравнений, получим: x1 = 12, x2 = 6 Откуда найдем максимальное значение целевой функции: F(X) = 480*12 + 350*6 = 7860 Задание 3.
Z(x) = x1+3x2+1→ max 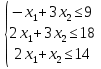 x1≥0, x2≥0 Решение 1)Вид: стандартная задача линейного программирования 2)Симплексная форма -1x1 + 3x2 + 1x3 + 0x4 + 0x5 = 9 2x1 + 3x2 + 0x3 + 1x4 + 0x5 = 18 2x1 + 1x2 + 0x3 + 0x4 + 1x5 = 14 3) Определим максимальное значение целевой функции F(X) = x1+3x2+1 при следующих условиях-ограничений. При вычислениях значение Fc = 1 временно не учитываем. -x1+3x2≤9 2x1+3x2≤18 2x1+x2≤14 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5. -x1+3x2+x3 = 9 2x1+3x2+x4 = 18 2x1+x2+x5 = 14 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Решим систему уравнений относительно базисных переменных: x3, x4, x5 Полагая, что равны 0, получим первый опорный план: X0 = (0,0,9,18,14) Базисное решение называется допустимым, если оно неотрицательно.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
