Контрольная 1, вариант 3 Задание Введите переменные
 Скачать 147.28 Kb.
|
Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 1 войдет переменная x2. Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x3 плана 0 на разрешающий элемент РЭ=3. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Таким образом, в новом плане 1 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
Разрешающий элемент равен (3) и находится на пересечении ведущего столбца и ведущей строки.
Пересчет симплекс-таблицы. Расчет каждого элемента в виде таблицы:
Получаем новую симплекс-таблицу:
Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 3, x2 = 4 F(X) = 1•3 + 3•4 + 1 = 16 4) Решение графически F(x) = x1+3x2+1→ max 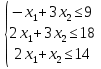 x1≥0, x2≥0 Построим область допустимых решений 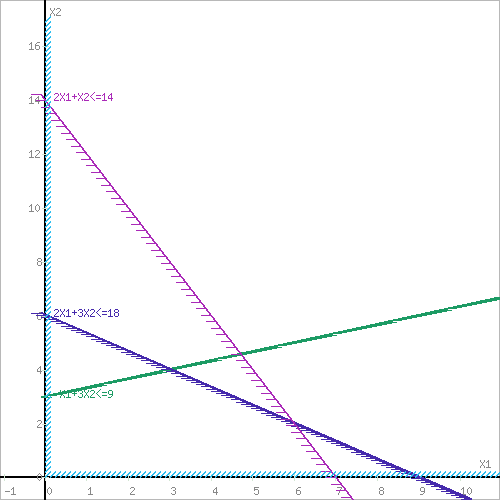 Или 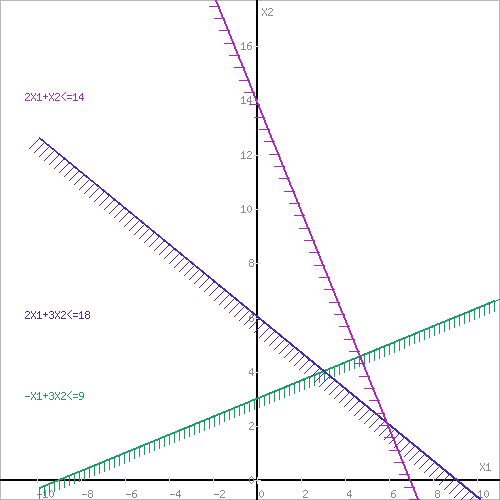 Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 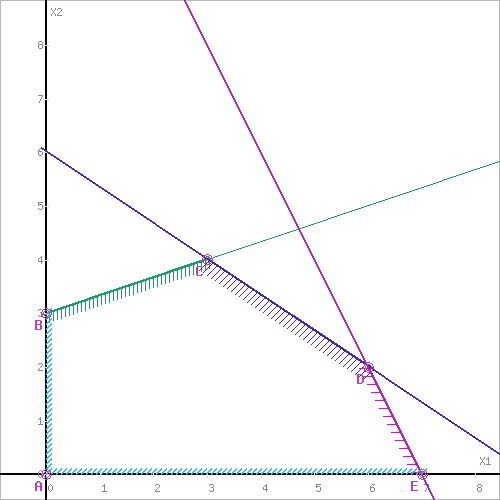 Рассмотрим целевую функцию задачи F = x1+3x2+1 → max. Построим прямую, отвечающую значению функции F = x1+3x2+1 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1;3). 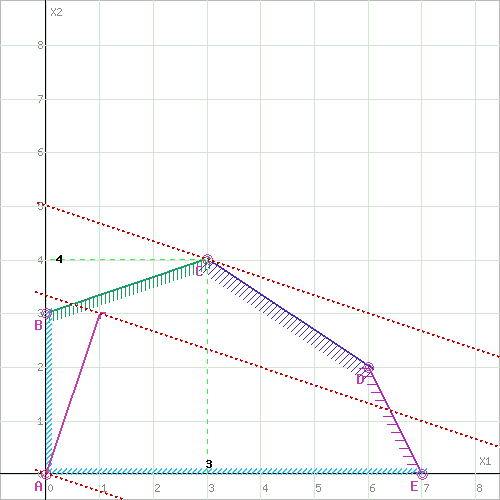 Прямая F(x) = const пересекает область в точке C. -x1+3x2=9 2x1+3x2=18 Решив систему уравнений, получим: x1 = 3, x2 = 4 Откуда найдем максимальное значение целевой функции: F(X) = 1*3 + 3*4 + 1 = 16 Задание 4.
Рацион некоторого животного должен в день содержать не менее b1 сумму углеводов и b2 единиц протеина. Для составления рациона имеется три основных вида продуктов. Продукт I стоит -  с1 за единицу, продукт II – с2 за единицу, продукт III– с3 за единицу. Продукт I содержит а11 единиц углеводов и а12 единиц протеина. Продукт II содержит а21 единиц углеводов и а22 единиц протеина. Продукт III содержит а31 единиц углеводов и а32 единиц протеина. Определить самую дешевую комбинацию продуктов, которая удовлетворит необходимым ограничениям (см. табл. 10).Таблица 10
Решение
1) Обозначим через х1,х2 ,х3, количество продукта, необходимого к потреблению. 2) Целевая функция : 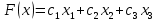 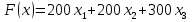 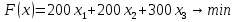 3) Система ограничений: 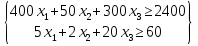 При этом х1,х2 ,х3≥0 Решим прямую задачу линейного программирования двойственным симплексным методом, с использованием симплексной таблицы. Приведем систему ограничений к системе неравенств смысла ≤, умножив соответствующие строки на (-1). Определим минимальное значение целевой функции F(X) = 200x1+200x2+300x3 при следующих условиях-ограничений. -400x1-50x2-300x3≤-2400 5x1+2x2+20x3≤60 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных -400x1-50x2-300x3+x4 = -2400 5x1+2x2+20x3+x5 = 60 Решим систему уравнений относительно базисных переменных: x4, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0,0,0,-2400,60)
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||