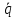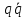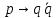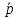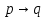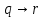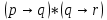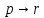кр.логика. Контрольная работа Задание Установить является ли предложение высказыванием, и если является истинно оно или ложно
 Скачать 119.22 Kb. Скачать 119.22 Kb.
|
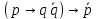
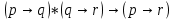
Задание 2. Доказать следующие правила вывода. Привести примеры. Правило заключения Правило отрицания Правило контрапозиции Правило расширенной контрапозиции Правило силлогизма Решение. Правило заключения 1  2 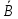 3 А – допущение 4 В – 1,3 Правило отрицания 1  2 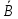 3 А – допущение 4 В – 1,3 5 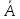 - А и 2,4 - А и 2,4Правило контрапозиции 1 A->B – П 2 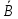 - допущение - допущение3  – 1,2 – 1,24  – В и 2,3 – В и 2,3Правило расширенной контрапозиции 1 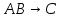 - П - П2 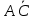 – допущение – допущение3 А – У.К.2 4 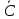 - У.К.2 - У.К.25  – 1,4 – 1,46 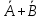 – 5 – 57  - 3 - 38 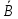 – 6,7 – 6,79 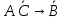 – В и 2,8 – В и 2,8Правило силлогизма 1  2 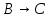 3 А – допущение 4 В – 1,3 5 С – 2,4 6  - В и 3,5 - В и 3,5Приведем пример умозаключения, выполненного по правилу заключения: «Если запись числа х оканчивается цифрой 5, то число х делится на 15. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5». Приведем пример умозаключения, выполненного по правилу отрицания: «Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5». Рассмотрим пример умозаключения, построенного по правилу силлогизма: «Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3». Пример по правилу контрапозиции: Если это вещество фосфор, то оно непосредственно с водородом не соединяется. Пример по правилу расширенной контрапозиции: Если у меня были деньги и я на каникулы не поехала домой, то, следовательно, я не была здорова. Задание 3. Приемы преобразования формул. Доказать тождественную истинность. Примеры преобразований Решение. Введение дизъюнкции 1 А 2 В 3 А+В – 1,2 (А+В) - > (А+В) – тавтология Если я человек, значит, я человек Удаление дизъюнкции 1 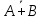 2 А – допущение 3 А+В – В.Д. 4 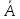 - А и 1,3 - А и 1,35 В – допущение 6 А+В – В.Д. 7 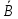 – А и 1,6 – А и 1,68 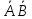 - В.К. 4,7 - В.К. 4,7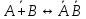 Он не может бегать или прыгать Он не может бегать и не может прыгать
Введение конъюнкции 1 А 2 В 3 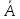 4 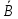 3 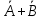 – 3,4 – 3,44  - 3 - 3АВ - > AB - тавтология Если я студент и отличник, значит, я студент и отличник Удаление конъюнкции 1  2 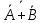 – допущение – допущение3  – О.Д.2 – О.Д.24  – У.К.3 – У.К.35 А – У.О.4 6 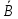 – У.К.3 – У.К.37 В – У.О.6 8  - В.К. 5,7 - В.К. 5,79 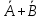 – С.А. 1,8, У.О. – С.А. 1,8, У.О. Я не студент и отличник. Я не студент или не отличник.
Задание 4. Доказать теорему дедукции на примере n=5 Если 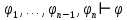 , то , то 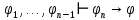 Решение. 1 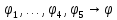 2 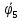 – допущение – допущение3 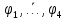 – З.О. 1,2 – З.О. 1,24 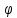 - допущение - допущение6 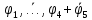 + +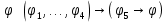 - 2,3,4 - 2,3,4Задание 5. Доказать правильность или неправильность рассуждений Если многоугольник – правильный, то в него можно вписать окружность; данный многоугольник не есть правильный, следовательно, в него нельзя вписать окружность Если диагонали данного параллелограмма взаимно перпендикулярны то этот параллелограмм - ромб; в данном параллелограмме диагонали взаимно не перпендикулярны; следовательно, он не есть ромб Если многоугольник правильный, то в него можно вписать окружность; в многоугольник можно вписать окружность; следовательно, он правильный Если диагонали данного параллелограмма взаимно перпендикулярны, то этот параллелограмм – ромб; следовательно, его диагонали взаимно перпендикулярны. |