математика методичка. Контрольная работа 1 для студентов 1го курса заочной формы обучения технических специальностей
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Часть 1 Линейная алгебра Решить уравнение 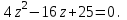 Решение. Решая формально квадратное уравнение, получим, пользуясь понятием мнимой единицы: 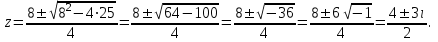 Ответ: 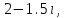 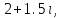 Вычислить 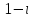 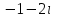 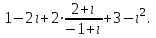 Решение. Последовательно проводя алгебраические операции, получим: 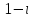 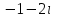 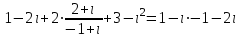 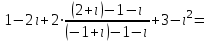 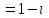 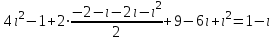 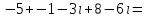 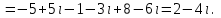 Ответ: 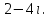 Вычислить  если: если: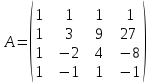 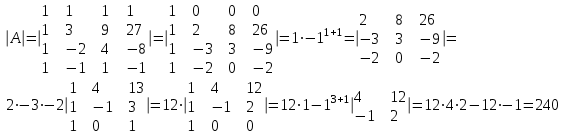 Ответ: 240. Решить систему методом Крамера 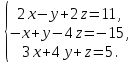 Решение. Сначала вычислим определитель системы (см. тему 1.5.2): 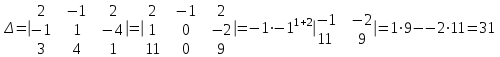 Так как определитель системы отличен от нуля, то решение системы возможно по правилу Крамера, для чего вычислим побочные определители: 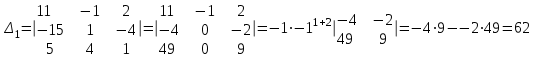 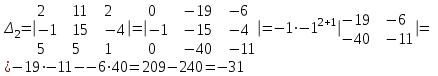 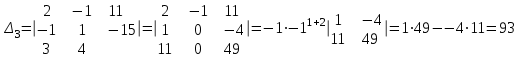 Поэтому 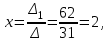 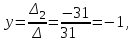 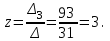 Ответ: x=2; y=-1; z=3. Решить систему матричным методом 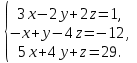 Решение. Сначала вычислим определитель системы (см. тему 1.5.1): 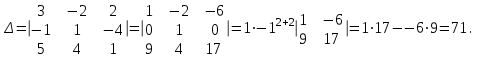 Так как определитель системы отличен от нуля, то решение системы возможно матричным методом, для чего вычислим для матрицы A обратную: Имеем 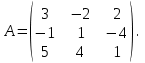 Составим матрицу из алгебраических дополнений элементов матрицы A и транспонируем ее: 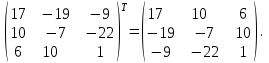 Тогда 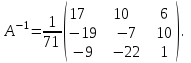 Так как решением системы AX=F является X=A -1 F, то 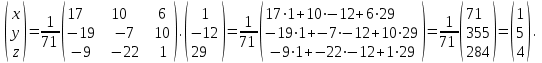 Ответ: x=1; y=5; z=4. Решить систему методом Гаусса 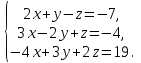 Решение. Метод Гаусса (см. тему 1.5.3): заключается в последовательном исключении неизвестных, поэтому исключим из второго x и третьего уравнений x, для чего вычтем из второго уравнения первое, умноженное на 3/2, а к третьему прибавим первое умноженное на 2. 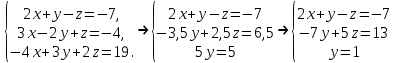 Из второго уравнения найдем z, а из первого x. 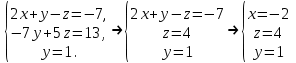 Ответ: x=-2; y=1; z=4. Решить систему 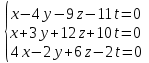 Решение. Решаем данную однородную систему (см. тему 1.5.4) методом Гаусса: 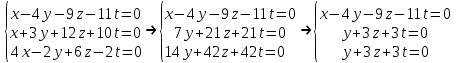 Так как третье уравнение является следствием первых двух уравнений, то система является неопределенной, поэтому обозначим «свободные» неизвестные z=l и t=m выразим x и y через l и m. 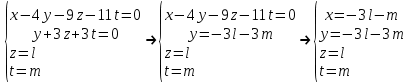 И общее решение искомой системы: Ответ: x=-3l-m; y=-3l-3m; z=l;t=m. Решить уравнение XA=B, Где 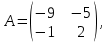 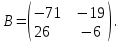 Решение. Если A -1 - обратная матрица для матрицы A, то X=BA-1. Найдем A -1. Так как 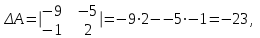 то A-1 существует. то A-1 существует.Составим матрицу из алгебраических дополнений элементов матрицы A: 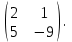 Тогда Тогда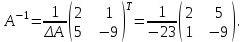 Поэтому Поэтому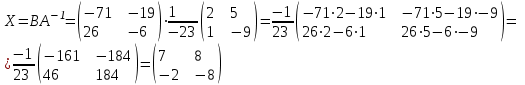 Ответ: 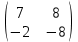 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку M(3;2) и перпендикулярной прямой y=-2x+9. Решение. Уравнение прямой, проходящей через заданную точку (см. (2.16)), имеет вид y-y1=k(x-x1) y-2=k(x-3). Так как условие перпендикулярности прямых (см. (2.13)) имеет вид: k1k2=-1, то (-2)k=-1, k=1/2. Поэтому искомое уравнение имеет вид: 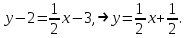 Ответ: 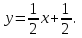 Даны вершины треугольника A(12;-4), B(0;5), C(-12;-11). Написать уравнения сторон и медианы, проведенной из точки A. Решение. Уравнение прямой, проходящей через две заданные точки (см. (2.17)), имеет вид 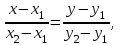 поэтому поэтому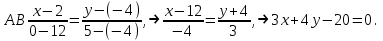 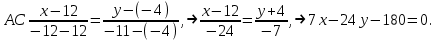 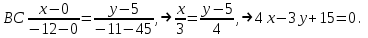 Пусть медиана, проведенная из точки A, пересекает BC в точке D. Координаты точки D найдем по формулам деления отрезка в данном отношении (см. (2.19)). 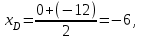 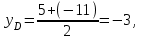 Запишем уравнение прямой AD через две точки: 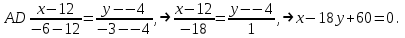 Ответ: AB 3x+4y-20=0; AC 7x-24y-180=0; BC 4x-3y+15=0; AD x+18y+60 Найти расстояние от точки M(1;2) до прямой 3x-4y+15=0. Решение. Расстояние от точки до прямой (см. (2.18)), найдем по формуле 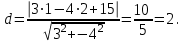 Ответ: 2. Даны координаты вершин треугольника A(12;-4), B(0;5), C(-12;-11). Найти угoл B. Решение. Запишем сначала уравнения сторон AB и BC. Уравнение прямой, проходящей через две заданные точки (см. (2.17)), имеет вид 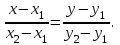 поэтому поэтому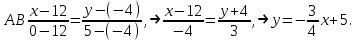 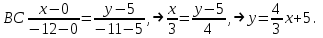 Так как прямые перпендикулярны, то угол B=90. Ответ: 90. Даны координаты вершин пирамиды A(3;1;4), B(-1;6;1), C(-1;1;6), D(0;4;-1). Найти ее объем. Решение. Так как объем пирамиды равен одной шестой объема параллелепипеда, построенного на векторах 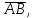 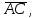 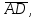 как на ребрах, то найдем координаты этих векторов и вычислим их смешанное произведение как на ребрах, то найдем координаты этих векторов и вычислим их смешанное произведение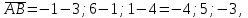 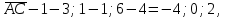 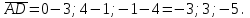 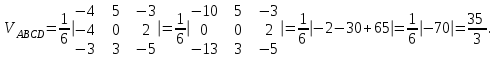 Ответ: 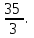 Найти уравнение эллипса, большая полуось которого равна a=0,5, а эксцентриситет равен =0,6. Решение. Эксцентриситет эллипса равен (см. (2.22)): 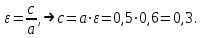 Так как b2=a2 -c2=0,25-0,09=0,16, то уравнение эллипса:  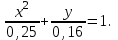 Ответ: 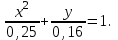 Вычислить угол между плоскостями 4x-5y+3z-1=0 и x-4y-z+9=0. Решение. Вектор нормали к первой плоскости: (4,-5,3), ко второй плоскости: (1,-4,-1). Тогда угол между ними (и одновременно угол между плоскостями) равен (см. (3.10): 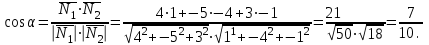 Ответ: 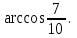 Дан тетраэдр A(-1;2;5), B(0;-4;5), C(-3;2;1), D(1;2;4). Написать уравнение прямой, проходящей через вершину D и параллельной стороне BC. Решение. Направляющий вектор стороны BC равен: (-3,6,-4). Этот вектор одновременно является направляющим и к искомой прямой. Уравнение данной прямой (см. (3.12)), поэтому, имеет вид: 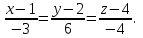 Ответ: 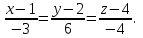 5. Контрольная работа № 1 Вариант 1. Часть 1 Линейная алгебра Решить уравнение 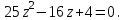 Вычислить 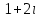 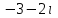 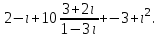 Вычислить определитель 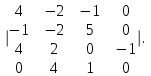 Решить систему уравнений методом Крамера 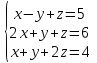 Решить систему уравнений матричным методом 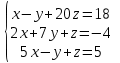  Решить однородную систему уравнений  Решить матричное уравнение   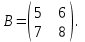 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (3, 2) перпендикулярно прямой 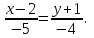 Составить уравнения сторон треугольника с вершинами А (2, -1), B (-1, 3), C (2, 4). Найти расстояние от точки А (3, 1) до прямой 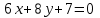 Найти угол A в треугольнике с вершинами А (4, 0), B (2, 4), C (-2, 0). Найти объем пирамиды, построенной на векторах 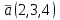 , , 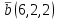 , , 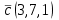 как на сторонах. как на сторонах.Написать уравнение окружности радиуса R=8 с центром в точке C(2,-5). Написать уравнение плоскости, проходящей через точку А(-1;5;-7) и отсекающую на осях координат равные отрезки. Даны координаты вершин пирамиды: A(4;2;5), B(0;7;2), C(0;2;7), D(1;5;0). Найти уравнение высоты, опущенной из вершины D на грань ABC. Вариант 2 Часть 1 Линейная алгебра Решить уравнение 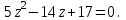 Вычислить 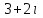 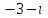 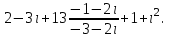 Вычислить определитель 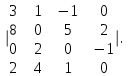 Решить систему уравнений методом Крамера 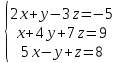 Решить систему уравнений матричным методом 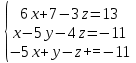 Решить систему уравнений методом Гаусса 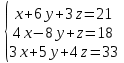 Решить однородную систему уравнений 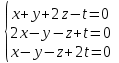 Решить матричное уравнение 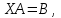 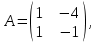 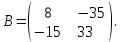 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (4, 4) параллельно прямой 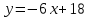 Составить уравнения сторон треугольника с вершинами А (-1, -1), B (2, 1), C (3, 4). Найти расстояние от точки А (3, 2) до прямой 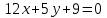 Найти угол В в треугольнике с вершинами А (2, 2), B (7, 8), C (5, 3). Найти объем пирамиды с вершинами А (2, 0, 0), B (0, 3, 0), C (0, 0, 6), D (2, 3, 8). Составить уравнение окружности радиуса R=7, проходящей через точки А(7, 7) и В(2, 4). Написать уравнение плоскости, проходящей через точки M(0;1;1) и N(2;0;1) перпендикулярно плоскости 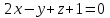 Составить канонические уравнения прямой, проходящей через точку (2;0;-3) параллельно прямой 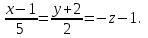 Вариант 3. Часть 1 Линейная алгебра Решить уравнение 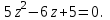 Вычислить 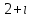 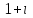 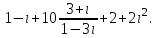 Вычислить определитель 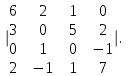 Решить систему уравнений методом Крамера 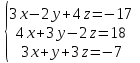 Решить систему уравнений матричным методом  Решить систему уравнений методом Гаусса  Решить однородную систему уравнений  Решить матричное уравнение  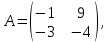 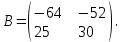 |
