математика методичка. Контрольная работа 1 для студентов 1го курса заочной формы обучения технических специальностей
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (7, 1) перпендикулярно прямой 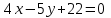 Составить уравнения сторон треугольника с вершинами 44 А (1, 0), B (3, 2), C (5, -2). Найти расстояние от точки А (5, 0) до прямой 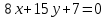 Найти угол между прямыми, заданными уравнениями 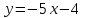 и и 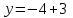 Найти объем пирамиды с вершинами А (0, 0, 0), B (5, 2, 0), C (2, 5, 0), D (1, 2, 4). Составить уравнение эллипса, проходящего через точку M (-2, 2) и имеющего большую полуось a=4. На расстоянии трех единиц от плоскости 3x-6y-2z+14=0 проведена параллельная ей плоскость. Написать ее уравнение. Составить канонические уравнения прямой, проходящей через точку (2;0;-3) параллельно оси OY. Вариант 4. Часть 1 Линейная алгебра Решить уравнение 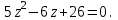 Вычислить 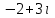 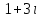 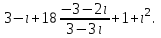 Вычислить определитель 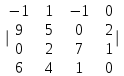 Решить систему уравнений методом Крамера 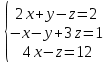 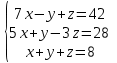 Решить систему уравнений методом Гаусса 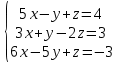 Решить однородную систему уравнений 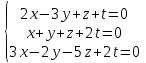 Решить матричное уравнение 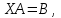 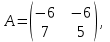 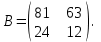 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (6, 1) параллельно прямой 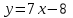 Составить уравнения сторон треугольника с вершинами А (1, -2), B (5, 4), C (-2, 0). Найти расстояние от точки А (4, 1) до прямой 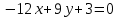 Найти угол между прямыми, заданными уравнениями 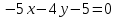 и и 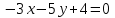 Найти объем пирамиды с вершинами А (2, 2, 2), B (4, 3, 3), C (4, 5, 4), D (5, 5, 6) Составить уравнение эллипса, если его большая полуось a=5 и эксцентриситет e=0,6 На оси z найти точку, равноудаленную от двух плоскостей: x+4y-3z-2=0 и 5x+z+8=0. Даны вершины треугольника A(2;-1;-3), B(5;2;-7), C(-7;11;6). Написать уравнение биссектрисы, проведенной из вершины A. Вариант 5. Часть 1 Линейная алгебра Решить уравнение 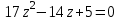 Вычислить 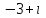 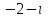 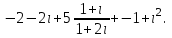 Вычислить определитель 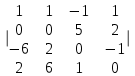 Решить систему уравнений методом Крамера 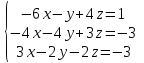 Решить систему уравнений матричным методом 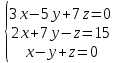 Решить систему уравнений методом Гаусса 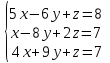 Решить однородную систему уравнений 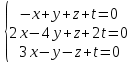 Решить матричное уравнение 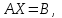 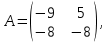 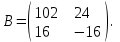 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (4, -4) перпендикулярно прямой 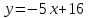 Составить уравнения сторон треугольника с вершинами А (1, -1), 47 B (3, 5), C (-2, 1). Найти расстояние от точки А (-3, 1) до прямой 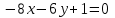 Найти угол C в треугольнике с вершинами А (3, 5), B (1, -1), C (-2, 1). Найти объем пирамиды, построенной на векторах 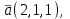 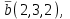 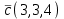 как на сторонах. как на сторонах.Составить уравнение гиперболы, если расстояние между ее фокусами равно 26, а эксцентриситет e=13/12. Найти расстояние между плоскостями x-2y+2z-17=0 и x-2y+2z+13=0. Найти угол между прямыми 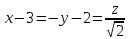 и и 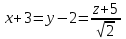 Вариант 6. Часть 1 Линейная алгебра Решить уравнение 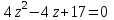 Вычислить 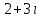 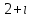 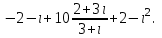 Вычислить определитель 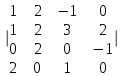 Решить систему уравнений методом Крамера 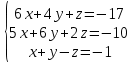 Решить систему уравнений матричным методом 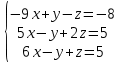 Решить систему уравнений методом Гаусса 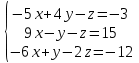 Решить однородную систему уравнений 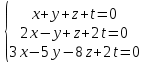 Решить матричное уравнение 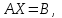 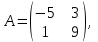 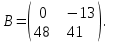 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (3, 2) параллельно прямой 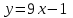 Составить уравнения сторон треугольника с вершинами А (5, 4), B (1, -2), C (-2, 0) Найти расстояние от точки А (2, 7) до прямой 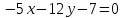 Найти угол между прямыми, заданными уравнениями 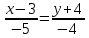 и и 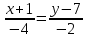 Найти объем пирамиды, построенной на векторах 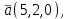 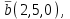 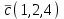 как на сторонах. как на сторонах.Составить уравнение эллипса, если даны точка эллипса ( 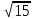 ;1) и расстояние между фокусами 2c=8. ;1) и расстояние между фокусами 2c=8.Написать уравнение плоскости, проходящей через точку А(-1;5;-7) и отсекающую на осях координат равные отрицательные отрезки Даны координаты вершин пирамиды: A(4;4;10), B(4;10;2), C(2;8;4), D(9;6;9). Найти уравнение высоты, опущенной из вершины D на грань ABC. Вариант 7. Часть 1 Линейная алгебра Решить уравнение 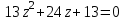 Вычислить 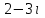 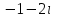 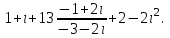 Вычислить определитель 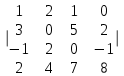 Решить систему уравнений методом Крамера 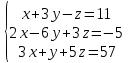 Решить систему уравнений матричным методом 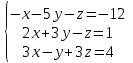 Решить систему уравнений методом Гаусса 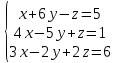 Решить однородную систему уравнений 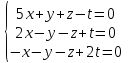 Решить матричное уравнение 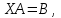 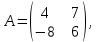 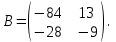 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (3, 1) перпендикулярно прямой 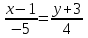 Составить уравнения сторон треугольника с вершинами А (4,0), B (2,4), C (-2,0). Найти расстояние от точки А (-7,2) до прямой 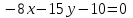 . .Найти угол A треугольника с вершинами А (1,-2), B (5,4), C (-2,0). Найти объем пирамиды, построенной на векторах 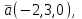 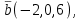 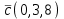 как на сторонах как на сторонахСоставить уравнение эллипса, если даны точка эллипса (2,-5/3) и его эксцентриситет ε=2/3 Написать уравнение плоскости, проходящей через ось OZ и образующей с плоскостью 2x+y-50,5z-7=0 угол 60 градусов. Составить канонические уравнения прямой, проходящей через точку (0;-1;-3) параллельно прямой 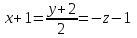 Вариант 8. Часть 1 Линейная алгебра Решить уравнение 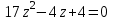 Вычислить 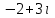 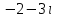 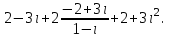 Вычислить определитель 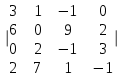 Решить систему уравнений методом Крамера 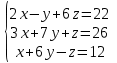 Решить систему уравнений матричным методом 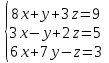 Решить систему уравнений методом Гаусса 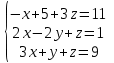 Решить однородную систему уравнений 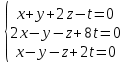 Решить матричное уравнение 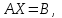 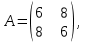 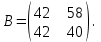 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (-1, 1) параллельно прямой 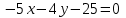 Составить уравнения сторон треугольника с вершинами А (-4,2), B (5,0), C (2,-5). Найти расстояние от точки А (5,1) до прямой 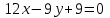 Найти угол между прямыми, заданными уравнениями 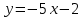 и и 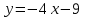 Найти объем пирамиды, построенной на векторах 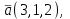 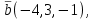 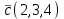 как на сторонах. как на сторонах.Составить уравнение эллипса, если его большая полуось a=8 и эксцентриситет e=0,5. На расстоянии двух единиц от плоскости x-6y-z+14=0 проведена параллельная ей плоскость. Написать ее уравнение. Составить канонические уравнения прямой, проходящей через точку (0;7;4) параллельно оси OX. Вариант 9. Часть 1 Линейная алгебра Решить уравнение 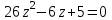 Вычислить 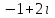 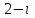 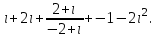 Вычислить определитель 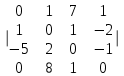 Решить систему уравнений методом Крамера 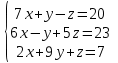 Решить систему уравнений матричным методом 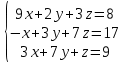 Решить систему уравнений методом Гаусса 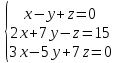 Решить однородную систему уравнений 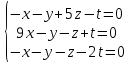 Решить матричное уравнение 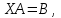 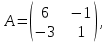 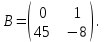 Часть 2 Аналитическая геометрия Составить уравнение прямой, проходящей через точку А (3,2) перпендикулярно прямой 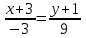 Составить уравнения сторон треугольника с вершинами А (-1,3), B (2,5), C (7,-5). Найти расстояние от точки А (3,4) до прямой 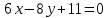 Найти угол B треугольника с вершинами А (7,4), B (7,8), C (2,2). Найти объем пирамиды с вершинами А (4,4,10), B (4,10,2), C (2,8,4), D (9,6,9). Составить уравнение гиперболы, если расстояние между ее фокусами равно 26, а эксцентриситет e=13/12. На оси y найти точку, равноудаленную от двух плоскостей: 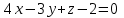 и и 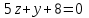 . .Даны вершины треугольника A(2;-1;-3), B(5;2;-7), C(-7;11;6). Написать уравнение медианы, проведенной из вершины A. Вариант 10. Часть 1 Линейная алгебра Решить уравнение 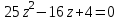 Вычислить 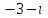 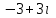 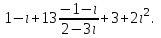 Вычислить определитель 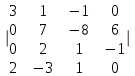 Решить систему уравнений методом Крамера 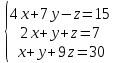 Решить систему уравнений матричным методом 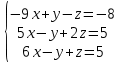 Решить систему уравнений методом Гаусса 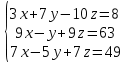 Решить однородную систему уравнений 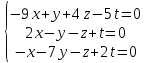 Решить матричное уравнение 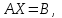 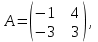 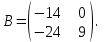 |
