математика методичка. Контрольная работа 1 для студентов 1го курса заочной формы обучения технических специальностей
 Скачать 0.96 Mb. Скачать 0.96 Mb.
|
|
ВЫСШАЯ МАТЕМАТИКА (математика – 1) Методические указания и контрольная работа № 1 для студентов 1-го курса заочной формы обучения технических специальностей Составители: Ю.А.Гусман, С.В.Мичурин, А.О.Смирнов Рецензенты: доктор физ.-мат. наук, профессор В.Г.Фарафонов Методические указания и контрольная работа № 1 предназначены для студентов 1-го курса заочной формы обучения технических специальностей. Излагаются основы теории линейной алгебры и аналитической геометрии; приведены варианты соответствующих контрольных заданий. Даны образцы выполнения типового контрольного задания. Подготовлены к публикации кафедрой высшей математики и рекомендованы к изданию редакционно-издательским советом Санкт-Петербургского государственного университета аэрокосмического приборостроения. Редактор Верстальщик Сдано в набор Подписано к печати Формат 60x84 1/16. Бумага офсетная. Печать офсетная. Усл.-печ. Л. Уч.- изд. Л. Тираж экз. Заказ № Редакционно-издательский центр ГУАП 190000 Общие методические указания Общий курс математики является фундаментом математического образования. Его изучение необходимо для успешного усвоения в дальнейшем общенаучных и специальных дисциплин. Основной формой обучения студента заочника является самостоятельная работа над учебным материалом, которая состоит из следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В помощь студентам- заочникам в университете организовано чтение лекций и практические занятия. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Завершающим этапом изучения отдельных частей курса высшей математики является сдача экзаменов. Курс высшей математики (математика – 1) изучается студентами 1-го курса технических факультет в первом и втором семестре. В первом семестре студенты сдают два экзамена: первый – по линейной алгебре и аналитической геометрии; второй – по дифференциальному и интегральному исчислению одной переменной. Во втором семестре студенты изучают теорию рядов, функций нескольких переменных, двойные и криволинейные интегралы. Для изучения теоретического материала и решения задач по этим темам рекомендуется следующая литература: 1. Привалов, И. И. Аналитическая геометрия / И.И.Привалов // «Лань», 2008. 304 с. 2. Беклемишев, Д.В. Курс аналитической геометрии и линейной алгебры / Д.В.Беклемишев //«Физматлит», 2008. 312 с. 3. Клетеник, Д.В. Сборник задач по аналитической геометрии / Д.В.Клетеник //«Профессия», 2010. 200 с. 4. Цубербиллер, О.Н. Задачи и упражнения по аналитической геометрии / О.Н.Цубербиллер // «Лань», 2007. 336 с. 5. Аналитическая геометрия: учеб. пособие / А.О. Смирнов, Ю.А. Гусман. – СПб.: ГУАП, 2012. 164 с. 6. Линейная алгебра: методические указания к решению контрольной работы № 1 / Н.А.Вешев, Г.М.Головачев, О.Е.Дик - СПб.: ГУАП, 2012. 34 с.__ В процессе изучения курса высшей математики студенты должны выполнить на первом курсе 3 контрольные работы. В первом семестре студенты выполняют две контрольные работы по математике. Данное пособие посвящено линейной алгебре и аналитической геометрии; выполнение 1-й контрольной работы покажет степень усвоения этой темы. Указания по выполнению контрольных работ Студент должен выполнять контрольные работы по заданным задачам конкретного варианта, номер которого получается из следующей формулы: следует разделить номер учебного шифра на 20, остаток от деления – номер варианта (если остаток 0, то номер варианта – 20). При оформлении и выполнении контрольных работ необходимо соблюдать следующие правила: 1. В начале работы должны быть ясно написаны фамилия студента, инициалы, номер студенческого билета, шифр, номер контрольной работы и дата отсылки работы в университет. 2. Контрольная работа выполняется в тетради, а не на листах, обязательно чернилами или шариковой ручкой (но не красными) с полями для замечаний рецензента. 3. Решения задач контрольной работы располагаются в порядке номеров, указанных в контрольных работах; перед решением задачи должно быть записано полностью ее условие, исходя из данных своего варианта задания. В том случае, когда несколько задач имеют общую формулировку, переписывая условие задачи, следует заменить общие данные конкретными из своего варианта. 4. Решения задач и объяснения к ним должны быть подробными, аккуратными, без сокращений слов; чертежи можно выполнять от руки. Получив из университета прорецензированную работу, студент должен исправить в ней все отмеченные ошибки и недочеты. Если работа не зачтена, она должна быть в короткий срок либо выполнена заново целиком, либо должны быть заново решены задачи, указанные рецензентом. Зачтенные контрольные работы предъявляют преподавателю на экзамене. Краткие теоретические сведения 1. Линейная алгебра 1.1 Алгебра комплексных чисел Первые представления о числе возникли из счета предметов. Результатом счета являются числа 1, 2, 3 и т.д. Они называются натуральными. В дальнейшем в связи с развитием алгебры были введены отрицательные числа и число нуль. Целые числа (натуральные числа 1, 2, 3 и т.д., отрицательные числа -1, -2, -3 и т.д. и нуль) и дроби ( 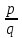 где p и q – целые числа) называются рациональными числами. Позднее к рациональным числам были добавлены иррациональные числа (действительно, например, величину гипотенузы равнобедренного прямоугольного треугольника с катетами равными единице нельзя выразить рациональным числом). где p и q – целые числа) называются рациональными числами. Позднее к рациональным числам были добавлены иррациональные числа (действительно, например, величину гипотенузы равнобедренного прямоугольного треугольника с катетами равными единице нельзя выразить рациональным числом).Рациональные и иррациональные числа называются действительными или вещественными. Напомним, что квадратное уравнение в случае неотрицательного дискриминанта имеет вещественные корни, в случае отрицательного дискриминанта в области вещественных чисел уравнение корней не имеет. В этом случае квадратное уравнение разрешимо в области комплексных чисел, которые ввел в середине 16-го века итальянский математик Кардано в связи с решением кубического уравнения. Комплексными числами называются числа вида z=x+iy, где x и y - вещественные числа, а i - мнимая единица, удовлетворяющая условию 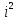 =-1. =-1.Так уравнение 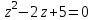 имеет решения имеет решения 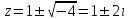 Числа x и y называются соответственно вещественной и мнимой частями Числа x и y называются соответственно вещественной и мнимой частямикомплексного числа z и обозначаются z=Rez и y=Imz.  Два комплексных числа z=x+iy и Два комплексных числа z=x+iy и 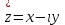 называются взаимно сопряженными. называются взаимно сопряженными.Комплексные числа геометрически можно интерпретировать точками z(x,y) плоскости комплексных чисел (z) или свободными векторами 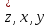 этой плоскости. (рис. 1.1) этой плоскости. (рис. 1.1)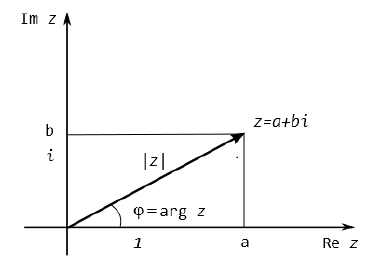 Рис. 1.1 Декартова и полярная система координат Комплексные числа можно представить как в алгебраической форме z=x+iy, так и в тригонометрической форме: 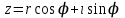 , ,где r и 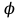 называются соответственно модулем и аргументом комплексного числа z: называются соответственно модулем и аргументом комплексного числа z: 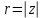 , , 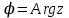 Отметим также и показательную форму комплексного числа: 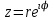 , ,где используется формула Эйлера: 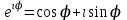 Аргумент числа z при 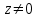 бесконечное значение, и все его значения отличаются друг от друга на слагаемые, кратные бесконечное значение, и все его значения отличаются друг от друга на слагаемые, кратные 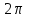 . При z=0 функция . При z=0 функция 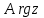 не определена. Из множества значений не определена. Из множества значений 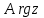 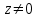 выделяют одно, лежащее в интервале выделяют одно, лежащее в интервале 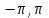 которое называют главным значением аргумента и обозначают символом argz. которое называют главным значением аргумента и обозначают символом argz.Числа 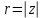 и и 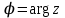 являются полярными координатами точки z. являются полярными координатами точки z.Условия равенства двух комплексных чисел z1 и z2 в полярных координатах будут 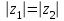 , , 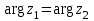 . .Действия над комплексными числами z1=x1+iy1 и z2=x2+iy2 определяются следующими равенствами: 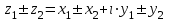 , ,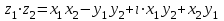 , ,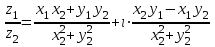 ; ; 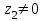 Если комплексные числа заданы в тригонометрической форме 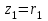 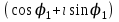 , , 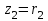 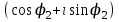 то их произведение находится по формуле то их произведение находится по формуле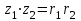 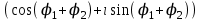 Аналогично определяется частное этих чисел при 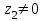 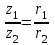 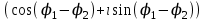 Возведение комплексного числа 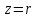 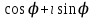 в натуральную степень проводится по формуле Муавра: в натуральную степень проводится по формуле Муавра: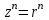 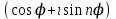 . .Корень n - ой степени из комплексного числа z имеет n различных значений, которые определяются формулой: 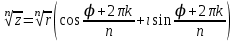 , где , где 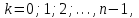 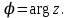 1.2 Матрицы; действия над ними 1.2.1 Основные определения Рассмотрим некоторую прямоугольную таблицу 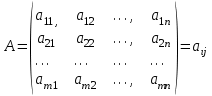 элементы, которой числа aij расположены в определенном порядке по m строкам и n столбцам. Двойной индекс ij указывает место элемента, т.е. номер строки i и номер столбца j, занимаемое этим элементом. Число строк и столбцов [mn] характеризует размеры матрицы. Матрица называется нулевой, если все ее элементы равны нулю. Две матрицы A и B называются равными, если они имеют одинаковые размеры (порядок) и равны их соответствующие элементы. Матрица B называется транспонированной по отношению к матрице A, если bij=aji, т.е. столбцы матрицы A являются строками матрицы B. Такая матрица обозначается AT . Матрица называется квадратной, если число ее строк равно числу столбцов. Квадратная матрица называется симметричной, если A=AT . В квадратной матрице диагональ ее, содержащая элементы aii, называется главной. Если в квадратной матрице все элементы главной диагонали равны единице, а все остальные элементы матрицы равны нулю, то матрица называется единичной и обозначается: 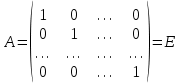 1.2.2 Линейные операции над матрицами Суммой матриц A и B одного порядка называется матрица C того же порядка, каждый элемент которой равен сумме соответствующих элементов данных матриц (C=A+B, если cij=aij+bij). Произведением матрицы A на число называется матрица B того же порядка, каждый элемент которой равен произведению числа на соответствующий элемент матрицы (B=A, если bij=aij). Матрица B называется противоположной матрице A , если сумма A и B есть нулевая матрица. Разностью матриц A и B одного порядка называется матрица C того же порядка, если B+C=A и обозначается A-B=C. Умножение матриц A и B определено, если число столбцов первой матрицы равно числу строк второй. Произведением двух матриц A размерами [mn] и B размерами [np] называется такая матрица C размерами [mp], каждый элемент которой cij равен сумме произведений элементов i - строки матрицы A и j - го столбца матрицы B. Пример 1.1 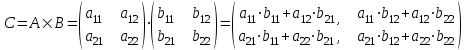 Пример 1.2 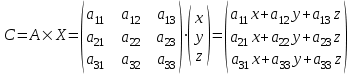 1.3 Определители Сопоставим квадратной матрице A некоторое число ∆A по определенному правилу. Определения (ради простоты) проведем для матриц порядка не более трех. Пусть матрица 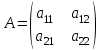 Тогда определитель второго порядка 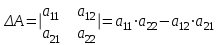 Сформулируем простейшие свойства определителей: Свойство 1. Величина определителя не изменится, если строки его заменить столбцами. Свойство 2. При перестановке местами двух строк (столбцов) определитель меняет знак на противоположный. Свойство 3 Множитель, общий для элементов какой-либо строки (столбца), можно вынести за знак определителя. Свойство 4. Величина определителя не изменится, если к элементам какойлибо строки (столбца) прибавить слагаемое, пропорциональное элементам другой строки (столбца). Свойство 5. Если в определителе какие-либо две строки (столбца) пропорциональны, то определитель равен нулю. Запишем определитель третьего порядка: 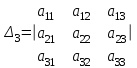 Минором ∆ij, , соответствующим элементу aij определителя (1.9), назовем определитель второго порядка, получаемый вычеркиванием i-той строки и j-того столбца. Алгебраическим дополнением, соответствующим элементу aij определителя (1.2), назовем число, равное (-1)i+j ∆ij, . Свойство 6. Определителем третьего порядка называется сумма произведений элементов какой-либо строки (столбца) на соответствующие алгебраические дополнения. Например, если раскладывать по первой строке: 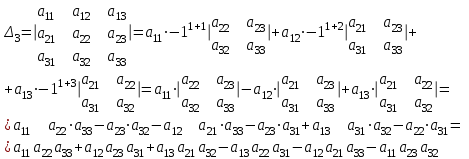 Для иллюстрации свойств определителя приведем вычисление конкретного определителя четвертого порядка: Пример 1.3 Вычислить определитель 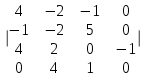 Решение. Применим разложение по четвертому столбцу, так как в нем наибольшее количество нулевых элементов. 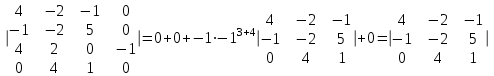 Вычтем из элементов второго столбца учетверенные элементы третьего столбца и разложим полученный определитель по элементам третьего столбца: 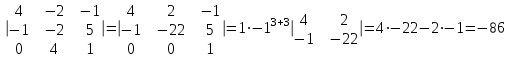 Ответ. -86 1.4 Обратная матрица Рассмотрим квадратную матрицу A размерами nn. Квадратная матрица B размера nn называется обратной для квадратной матрицы A, если выполнены условия AB=BA=E. Матрицу B принято обозначать B=A -1 . Эту матрицу можно найти, если определитель матрицы A отличен от нуля. Последовательность операций нахождения обратной матрицы, например, следующая: запишем союзную матрицу, состоящую из алгебраических дополнений матрицы A, транспонируем ее и делим на величину определителя матрицы A. Пример 1.4 Найти обратную матрицу для матрицы 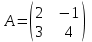 Решение. 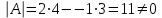 Союзная матрица имеет вид: 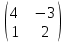 Транспонированная союзная матрица имеет вид: 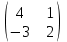 Обратная матрица 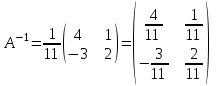 Ответ: 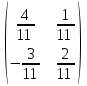 1.5 Разрешимость систем линейных уравнений Одной из характеристик матрицы является ранг матрицы. Рассмотрим произвольную матрицу A размера mn 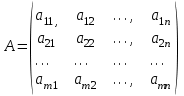 (1.10) (1.10)Вычеркивая то или иное количество строк и столбцов ее, можно получить квадратные матрицы различного порядка. Определители таких матриц назовем минорами различного порядка (в том числе минорами первого порядка назовем сами элементы матрицы A). Рангом матрицы A называется число r равное наивысшему порядку минора, отличного от нуля, который можно составить из элементов матрицы A. Системой из m линейных уравнений с n неизвестными называется система вида: 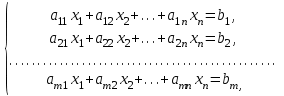 (1.11) (1.11)где aij - коэффициенты этой системы, x1, x2,…, 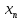 - неизвестные, b1, b2,…, - неизвестные, b1, b2,…,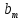 - свободные члены. Рассмотрим матрицу из коэффициентов при неизвестных, матрицу-столбец из неизвестных величин и матрицу-столбец из свободных членов системы (1.11), т.е. - свободные члены. Рассмотрим матрицу из коэффициентов при неизвестных, матрицу-столбец из неизвестных величин и матрицу-столбец из свободных членов системы (1.11), т.е.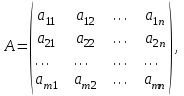 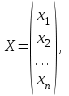 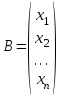 Тогда система (1.11) может быть записана в матричной форме: AX=B. (1.12) Наряду с матрицей A (1.10) введем матрицу 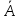 , которую будем называть расширенной матрицей системы (1.11): , которую будем называть расширенной матрицей системы (1.11):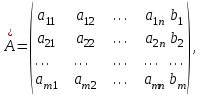 Теорема Кронекера-Капелли (теорема об условиях разрешимости линейных систем). Для совместности системы (1.11) необходимо и достаточно, чтобы ранг матрицы A, составленной из коэффициентов при неизвестных, был равен рангу расширенной матрицы 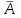 . Причем, в случае, если система (1.11) совместна (r(A)=r( . Причем, в случае, если система (1.11) совместна (r(A)=r(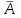 )), то: )), то: а) при r(A)<n система (1.11) имеет бесчисленное множество решений, при этом n-r(A) неизвестных этой системы могут быть произвольными, а остальные однозначно через них выражаются; б) при m=n и r(A)=n система (1.11) имеет единственное решение. 1.6 Решение линейных систем Рассмотрим методы решения систем (1.11) 1.6.1 Матричный способ решения квадратных систем Квадратной системой будем называть систему (1.11), если m=n. Если при этом определитель системы не равен нулю (∆A0), то система (1.12) AX=B может быть решена матричным методом по формуле: 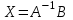 1.6.2 Правило Крамера Квадратную систему при m=n и определителе системы не равным нулю (∆A0) удобно решать и по правилу Крамера. Поясним правило Крамера на примере квадратной системы при n=3: 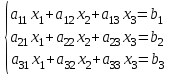 (1.15) (1.15)Определитель системы (1.15) 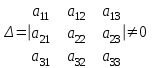 Назовем побочными определители, в которых соответствующий столбец заменен столбцом свободных членов: 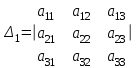 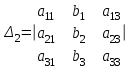 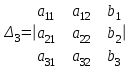 Тогда 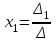 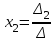 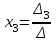 1.6.3 Метод Гаусса Приведенные выше решения системы линейных уравнений (матричным методом и методом Крамера) могут быть использованы лишь в том случае, когда число неизвестных равно числу уравнений и когда определитель системы отличен от нуля. Более общим, чем указанные выше методы, является метод Гаусса решения системы линейных уравнений или метод последовательного исключения неизвестных, так как он применим для любой системы из m уравнений с n неизвестными. Пусть 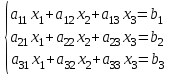 Если a11=0, то меняем уравнения местами так, чтобы коэффициент при первой переменной в первом уравнении стал, отличен от нуля. Теперь, если a110, то умножаем первое уравнение на 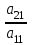 и вычитаем его из второго, а затем умножаем первое уравнение на и вычитаем его из второго, а затем умножаем первое уравнение на 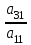 и вычитаем из третьего, после чего получаем и вычитаем из третьего, после чего получаем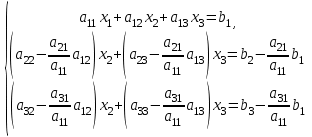 Отметим, что во втором и третьем уравнениях отсутствует первая переменная. Аналогично выше изложенному избавляемся в третьем уравнении от второй переменной и тогда система (1.17) примет вид: 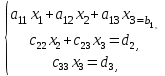 где c22, c23, c33, d2, d3 – новые коэффициенты системы и новые свободные члены. Если диагональные коэффициенты системы (1.18) отличны от нуля, то система имеет единственное решение, которое можно найти, решая данную систему «снизу вверх». Если при решении системы уравнений одно из них примет вид «0=0», то это уравнение можно исключить из рассмотрения. Если же в результате преобразования системы появится уравнение «0=b, b0,» не имеющее решений, то и вся система не будет иметь решений. Если в преобразованной системе число переменных будет больше числа уравнений, то часть переменных можно выбрать в качестве параметров так, чтобы число оставшихся переменных совпадало с числом уравнений, и чтобы диагональные коэффициенты новой системы были отличны от нуля. В этом случае система будет иметь бесконечно много решений. 1.6.4 Однородные системы Линейная система уравнений, в которой все свободные члены равны нулю, называется однородной: 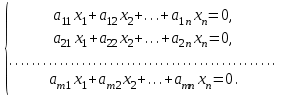 (1.19) (1.19)По теореме Кронекера-Капелли такая система всегда совместна, так как столбец из нулей не может увеличить ранг матрицы. Легко видеть, что (1.19) всегда имеет нулевое решение (т.е. состоящее из одних нулей). Если в (1.19) число уравнений совпадает с числом неизвестных, то если определитель системы отличен от нуля, то система имеет только нулевое решение. Если определитель системы равен нулю, то система имеет бесконечно много решений (и ненулевые). Если в (1.19) число уравнений больше числа неизвестных, то система имеет бесконечно много решений (естественно, среди них есть и ненулевые). 2 Аналитическая геометрия 2.1 Векторы, действия над ними Вектором в пространстве будем называть столбец из трех чисел. Любой вектор 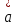 единственным образом раскладывается по координатным ортам единственным образом раскладывается по координатным ортам 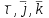 прямоугольной декартовой системы координат OXYZ: прямоугольной декартовой системы координат OXYZ: 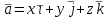 , где x,y,z - вещественные числа, называемые координатами вектора , где x,y,z - вещественные числа, называемые координатами вектора 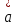 . Вектор . Вектор 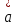 можно записывать: можно записывать: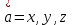 В геометрической интерпретации вектору можно сопоставить направленный отрезок прямой, один из концов которого объявлен началом, а другой – концом вектора. Если известны начало 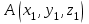 и конец и конец 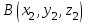 вектора вектора 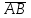 то его координаты вычисляются по формулам: то его координаты вычисляются по формулам: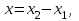 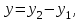 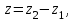 Длина вектора 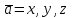 вычисляется по формуле вычисляется по формуле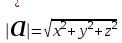 Векторы 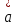 и и 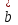 называются коллинеарными, если они параллельны одной прямой. Векторы называются коллинеарными, если они параллельны одной прямой. Векторы 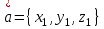 , ,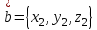 коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны: коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны: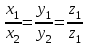 Векторы 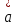 , , 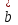 , , 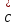 называются компланарными, если они параллельны одной плоскости. Условие компланарности векторов называются компланарными, если они параллельны одной плоскости. Условие компланарности векторов 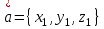 , ,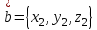 , , 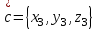 заключается в равенстве нулю определителя, построенного по их координатам: заключается в равенстве нулю определителя, построенного по их координатам: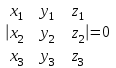 Из определения следует, что длина вектора 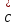 равна: равна: 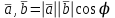 то есть произведению длины перемножаемых векторов на синус угла между ними. Таким образом, длина вектора то есть произведению длины перемножаемых векторов на синус угла между ними. Таким образом, длина вектора 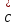 численно равна площади параллелограмма, построенного на векторах численно равна площади параллелограмма, построенного на векторах 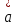 и и  . Этот вектор перпендикулярен плоскости, в которой лежат перемножаемые векторы, и направлен в соответствии с правилом «правого винта» при вращении первого вектора ко второму. Смешанным произведением трех векторов . Этот вектор перпендикулярен плоскости, в которой лежат перемножаемые векторы, и направлен в соответствии с правилом «правого винта» при вращении первого вектора ко второму. Смешанным произведением трех векторов  , , , , , называется число, равное векторному произведению , называется число, равное векторному произведению 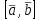 , умноженному скалярно на вектор , умноженному скалярно на вектор 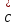 (обозначается (обозначается 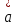 , ,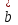 , , ). ). Если векторы  , , , , заданы своими координатами формулой: заданы своими координатами формулой: 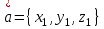 , ,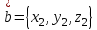 , ,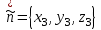 , то смешанное произведение определяется: , то смешанное произведение определяется: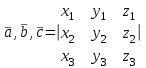 Геометрическое истолкование смешанного произведения: абсолютная величина смешанного произведения равна объему параллелепипеда, построенного на этих векторах как на ребрах (рисунок 2.1) 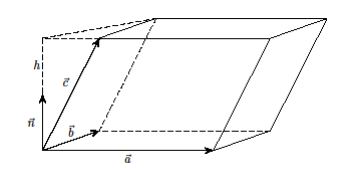 рис. 2.1 К определению векторного и смешанного произведения. Отметим, что объем треугольной пирамиды, построенной на векторах  , , , , равен одной шестой объема параллелепипеда. Условием компланарности векторов равен одной шестой объема параллелепипеда. Условием компланарности векторов 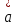 , ,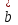 , ,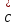 является равенство нулю их смешанного произведения. является равенство нулю их смешанного произведения.2.2 Прямая на плоскости Уравнением прямой на плоскости называется такое уравнение первой степени с переменными x и y, которому удовлетворяют координаты любой точки этой прямой. Общее уравнение прямой имеет вид: Ax+By+C=0 (2.8) Уравнение прямой, которое разрешено относительно переменной y, то есть уравнение вида: y=kx+b (2.9) называется уравнением прямой с угловым коэффициентом. Параметр k называется угловым коэффициентом и равен тангенсу угла наклона прямой к оси OX, k=tg. Параметр b - величина отрезка, отсекаемого прямой на оси, считая от начала координат. Уравнение вида 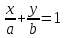 (2.10) называется уравнением прямой в отрезках, здесь a и b - величины отрезков, отсекаемых прямой на осях координат (рис. 2.2). (2.10) называется уравнением прямой в отрезках, здесь a и b - величины отрезков, отсекаемых прямой на осях координат (рис. 2.2).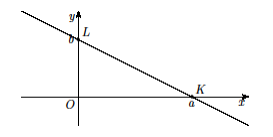 Рис. 2.2 Отрезки, отсекаемые на осях координат. Угол между двумя прямыми y=k1x+b1 и y=k2x+b2 вычисляется по формуле: 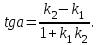 Условие параллельности двух прямых: k1=k2. (2.12) Условие перпендикулярности: k1k2=-1. (2.13) Если прямые даны уравнениями в общем виде: A1x+B1y+C1=0, A2x+B2y+C2=0. Условие параллельности прямых можно записать так: 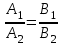 Условие перпендикулярности: A1A2+B1B2=0. (2.15) Если прямая имеет угловой коэффициент k и проходит через данную точку (x0,y0), то ее уравнение имеет вид: y-y0=k(x-x0). (2.16) Если прямая проходит через две данные точки (x1,y1), и (x2,y2), то уравнение 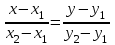 (2.17) (2.17)называется уравнением прямой, проходящей через две данные точки. Расстояние от точки (x0,y0) до прямой Ax+By+C=0 находится по формуле: 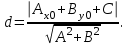 (2.18) (2.18)Деление отрезка в заданном отношении . Пусть M(x1,y1), и N(x2,y2), тогда координаты точки (x0,y0), такой, что 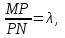 вычисляются по формулам: 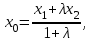 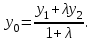 (2.19) (2.19)Длина отрезка MN находится по формуле: 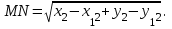 (2.20) (2.20)2.3 Кривые второго порядка Кривыми второго порядка являются: эллипс, гипербола и парабола. 2.3.1 Эллипс Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек (фокусов) есть величина постоянная. Каноническое (простейшее) уравнение эллипса имеет вид: 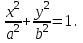 (2.21) (2.21)Координаты фокусов эллипса: F1(-c,0), F2(c,0), c2 =a2 -b2 . Вершины эллипса: A1(-a,0), A2(a,0), B1(0,-b), B2(0,b). Отрезки A1A2=2a, B1B2=2b называются соответственно большой и малой осями эллипса, величины a, b - большой (малой) полуосями эллипса (рис. 2.3). 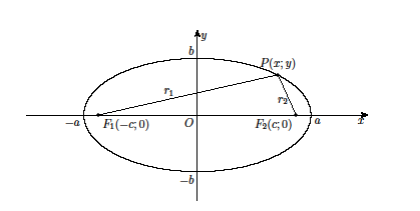 Рис. 2.3. Эллипс Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси эллипса и обозначается: 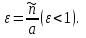 (2.22) (2.22)Директрисами эллипса называются две прямые, параллельные малой оси эллипса и отстоящие от нее на расстояния, равном 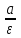 ; уравнения директрис: ; уравнения директрис: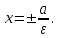 (2.23) (2.23)Фокальными радиусами называются расстояния r1 и r2 от произвольной точки M(x,y) эллипса до его фокусов F1 и F2 соответственно. Фокальные радиусы находятся по формулам: 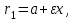 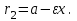 (2.24) (2.24)Отношение расстояний любой точки эллипса до фокуса и соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса: 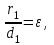 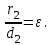 (2.25) (2.25)Окружность – вырожденный эллипс (с=0). Каноническое уравнение окружности имеет вид: (x-xc)2 +(y-yc)2 =r2 , (2.26) где (xc ,yc) - координаты ее центра, а r - ее радиус. Если центр окружности находится в начале координат, то ее уравнение имеет более простой вид: x2 +y2 =r2. (2.27) 2.3.2 Гипербола Гиперболой называется множество точек плоскости, разность расстояний которых до двух данных точек (фокусов) есть величина постоянная. Каноническое (простейшее) уравнение гиперболы имеет вид: 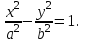 Координаты фокусов гиперболы: F1(-c,0), F2(c,0), c2 =a2 +b2 . Вещественной осью гиперболы называется отрезок A1A2=2a. Мнимой осью гиперболы называется отрезок B1B2=2b, где B1(0,-b), B2(0,b) (рис. 2.4). 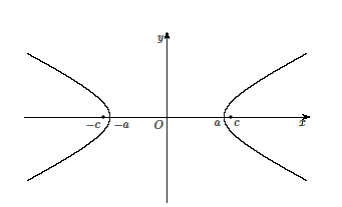 Рис. 2.4. Гипербола. Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине вещественной оси гиперболы и обозначается: 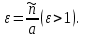 (2.29) (2.29)Директрисами гиперболы называются две прямые, параллельные мнимой оси гиперболы и отстоящие от нее на расстояния, равном 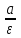 ; уравнения директрис: ; уравнения директрис: 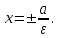 (2.30) (2.30)Фокальными радиусами называются расстояния r1 и r2 от произвольной точки M(x,y) гиперболы до его фокусов F1 и F2 соответственно. Фокальные радиусы находятся по формулам: Для точек M(x,y), лежащих на левой ветви гиперболы: 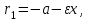 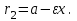 (2.31) (2.31) Для точек M(x,y), лежащих на правой ветви гиперболы: 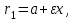 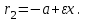 (2.32) (2.32) Асимптотами гиперболы являются диагонали прямоугольника, центр которого находится в центре гиперболы, а стороны равны и параллельны осям гиперболы. Уравнения асимптот гиперболы: 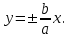 (2.33) Отношение расстояния r1 (или r2) от любой точки гиперболы до фокуса F1 (или F2) к соответствующему расстоянию d1 (или d2) от нее до директрисы есть величина постоянная, равная эксцентриситету: (2.33) Отношение расстояния r1 (или r2) от любой точки гиперболы до фокуса F1 (или F2) к соответствующему расстоянию d1 (или d2) от нее до директрисы есть величина постоянная, равная эксцентриситету: 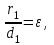 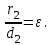 (2.34) (2.34)Сопряженной называется гипербола, фокусы которой расположены на оси OY: 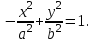 (2.35) (2.35)Равносторонней (равнобочной) называется гипербола с равными полуосями (a=b). 2.3.3 Парабола Параболой называется множество точек плоскости, равноудаленных от данной точки (фокуса) и данной прямой (директрисы) (рис. 2.5). 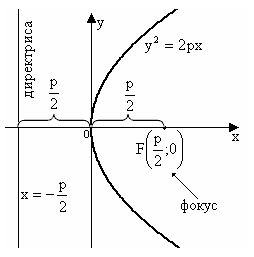 Рис. 2.5. Парабола Координаты фокуса параболы: F(p/2,0). Уравнение директрисы параболы: x=-p/2. Каноническое уравнение параболы: 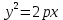 . (2.36) . (2.36) Фокальным радиусом называется расстояние r от произвольной точки M(x,y) параболы до ее фокуса F. Фокальный радиус находится по формуле: 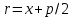 (2.37) (2.37)Отношение расстояния r от любой точки M(x,y) параболы до фокуса F к расстоянию d от нее до директрисы называется ее эксцентриситетом, и он равен 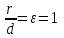 (по определению параболы). (по определению параболы).3 Аналитическая геометрия в пространстве Перед тем как рассмотреть такие пространственные объекты как плоскость и прямая в пространстве обобщим на пространственный случай формулы (2.19) и (2.20). Деление отрезка в заданном отношении . Пусть M(x1,y1,z1), и N(x2,y2,z2), тогда координаты точки P(x0,y0,z0), такой, что 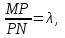 вычисляются по формулам: вычисляются по формулам: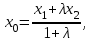 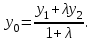 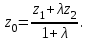 (3.1) (3.1)Длина отрезка MN находится по формуле: 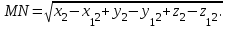 3.1 Плоскость В декартовых координатах каждая плоскость в трехмерном пространстве определяется уравнением первой степени относительно координат точки и каждое такое уравнение первой степени определяет плоскость. Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором (рис. 3.1).  Рис. 3.1. Плоскость Уравнение A(x-x0)+B(y-y0)+C(z-z0)=0 (3.3) определяет плоскость, проходящую через точку M0(x0,y0,z0) и имеющую нормальный вектор 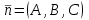 . .Введя обозначение D=-Ax0-By0-Cz0, получаем общее уравнение плоскости: Ax+By+Cz+D=0. (3.4) Если в общем уравнении плоскости D=0, то плоскость проходит через начало координат. Если какой-либо из коэффициентов A,B,C равен нулю, то плоскость параллельна той координатной оси, которая одноименна с отсутствующей координатой; если, кроме этого, D=0, то плоскость проходит через эту ось. Если какие-либо два из коэффициентов A,B,C равны нулю, то плоскость параллельна той координатной плоскости, которая проходит через оси, одноименные с отсутствующими координатами: если, кроме того, D=0, то плоскость совпадает с этой координатной плоскостью. Если в общем уравнении плоскости ни один из коэффициентов A,B,C,D не равен нулю то это уравнение может быть преобразовано к виду: 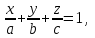 (3.5) (3.5)где величины a,b,c равны величинам отрезков, которые плоскость отсекает на координатных осях, это уравнение плоскости «в отрезках». Уравнение плоскости, проходящей через три данные точки M1(x1,y1,z1), M2(x2,y2,z2), M3(x3,y3,z3), не лежащие на одной прямой, имеет вид: 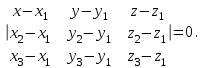 (3.6) (3.6)Расстояние от точки M0(x0,y0,z0) до плоскости, заданной общим уравнением, равно: 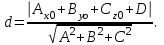 (3.7) (3.7)Пусть две плоскости заданы общими уравнениями: A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0. Тогда условие параллельности двух плоскостей: 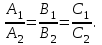 (3.8) (3.8)Условие перпендикулярности двух плоскостей: 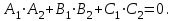 (3.9) (3.9)Угол между двумя плоскостями определяется как угол между нормалями к этим плоскостям: 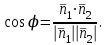 (3.10) (3.10)3.2 Прямая в пространстве Прямая в трехмерном пространстве определяется как линия пересечения двух плоскостей: 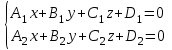 (3.11) (3.11)Канонические уравнения прямой: 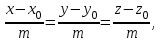 (3.12) (3.12)где x0,y0,z0 - координаты точки M0 на прямой; x,y,z – текущие координаты точек прямой; m,n,p – координаты направляющего вектора 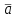 прямой (рис.3.2). прямой (рис.3.2).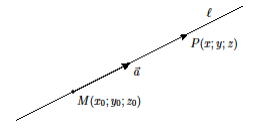 Рис. 3.2. Прямая в пространстве Параметрические уравнения прямой: 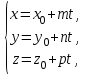 (3.13) (3.13)где t – переменный параметр, отмечающий точку прямой. Уравнения прямой, проходящей через две данные точки M(x1,y1,z1), и N(x2,y2,z2): 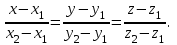 (3.14) (3.14)Если прямая задана как пересечение двух плоскостей, то направляющий вектор прямой определяется как векторное произведение нормалей искомых плоскостей: 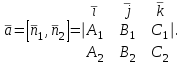 (3.15) (3.15)Пусть две прямые заданы каноническими уравнениями: 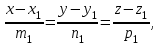 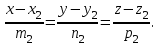 Тогда условие параллельности: 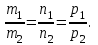 (3.16) (3.16)Условие перпендикулярности: 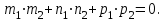 (3.17) (3.17)Угол между прямыми определяется как угол между направляющими векторами этих прямых: 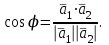 (3.18) (3.18)3.3 Взаимное расположение прямой и плоскости Пусть в пространстве заданы: прямая 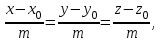 и плоскость Ax+By+Cz+D=0. Угол между прямой и плоскостью определяется посредством нахождения угла между направляющим вектором прямой 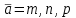 и вектором нормали к плоскости и вектором нормали к плоскости 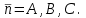 Тогда (рис.3.3) Тогда (рис.3.3)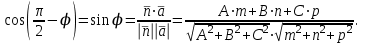 (3.19) (3.19)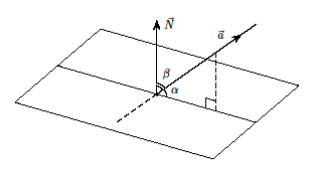 Рис.3.3. Прямая и плоскость. Условие параллельности прямой и плоскости есть условие перпендикулярности векторов 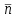 и и 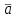 : :Am+Bn+Cp=0. (3.20) Условие перпендикулярности прямой и плоскости есть условие коллинеарности векторов 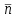 и и 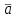 : :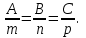 (3.21) (3.21)Условие принадлежности данной прямой данной плоскости: 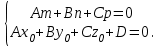 (3.22) (3.22)4. Решение типового варианта Вариант № 0 |
