Контрольная работа Определенный интеграл. Контрольная работа 1 по темеПервообразная и интеграл (Е. М. цикл) Цель работы знания таблицы и правил нахождения первообразных
 Скачать 0.81 Mb. Скачать 0.81 Mb.
|
|
Часть 1 При выполнении заданий части 1 в бланке ответов №1 под номером выполняемого вами задания А1– А10 поставьте знак « 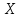 » в клеточку, номер которой соответствует номеру выбранного вами ответа. » в клеточку, номер которой соответствует номеру выбранного вами ответа.А1Упростите выражение 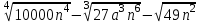 , если , если 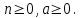 1) 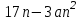 ; 2) ; 2) 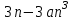 ; 3) ; 3) 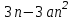 ; 4) ; 4) 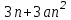 . .А2Найдите значение выражения 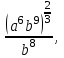 если если 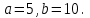 1) 6,25; 2) 625; 3) 25; 4) 12,5. А3Вычислите 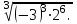 1) 12; 2) 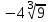 ; 3) ; 3)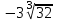 ;4) -12. ;4) -12.А4Упростите выражение 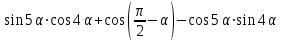 1) 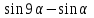 ; 2) ; 2)  ;3) 0; 4) ;3) 0; 4)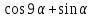 . .А5Укажите первообразную функции 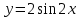 1) 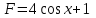 ; 2) ; 2) 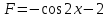 ; ;3) 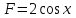 ; 4) ; 4) 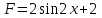 . .А6Найдите угловой коэффициент касательной, проведённой к графику функции 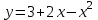 в его точке с абсциссой в его точке с абсциссой 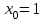 . .1) 0; 2) 4; 3) 1; 4) -2. А 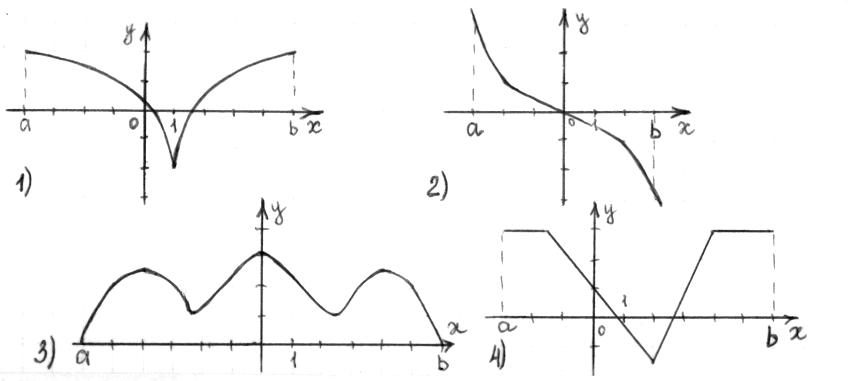 7На рисунке изображены графики функций, заданных на отрезках 7На рисунке изображены графики функций, заданных на отрезках 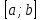 . Укажите график четной функции. . Укажите график четной функции.А8Укажите множество решений неравенства 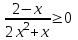 1) 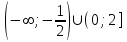 ; 2) ; 2)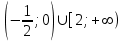 ; ; 3) 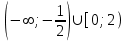 ; 4) ; 4) 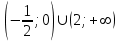 . .А9Укажите промежуток, которому принадлежат корни уравнения 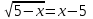 1  ) )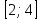 ; 2) ; 2) 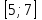 ; 3) ; 3) 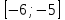 ; 4) ; 4) 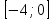 . .А10 Найдите площадь фигуры, ограниченной линиями 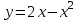 и у = 0 1) и у = 0 1)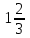 ; 2) ; 2)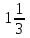 ; 3) ; 3)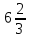 ; 4) 1. ; 4) 1.Часть 2 Ответом к каждому заданию этой части будет некоторое число. Это число надо вписать в бланк ответов №1 справа от номера задания (В1-В5), начиная с первой клеточки. Каждую цифру или знак минус отрицательного числа пишите в отдельной клеточке строго по образцу из верхней части бланка. Единицы измерений писать не нужно. Если ответ получится в виде дроби, то её надо округлить до ближайшего целого числа. В1Прикаком значении афункция 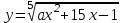 имеет максимум в точке х0 = 1,5? имеет максимум в точке х0 = 1,5?В2На рисунке изображён график производной функции 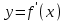 заданной на отрезке заданной на отрезке  . .Исследуйте функцию  на монотонность на монотонностьи в ответе укажите длину промежутка возрастания. 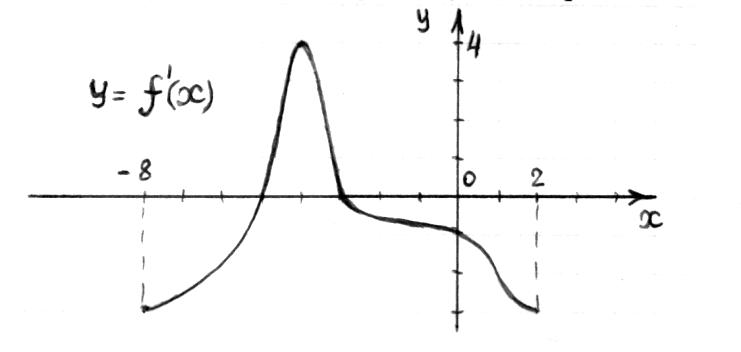 В3 Решите систему уравнений. Найдите х0+ у0 , если (х0; у0) – решение системы. 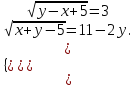 В4Решите уравнение 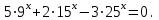 В5 Найдите число корней уравнения 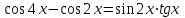 на промежутке на промежутке 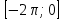 . . Часть 3 Для записи ответов к заданиям этой части(С1-С3) используйте бланк ответов №2. Запишите сначала номер задания, а затем полное решение. С1Решите уравнение 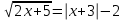 . .С2Решите уравнение 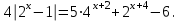 С3Найдите все значенияр, при которых уравнение 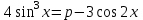 не имеет корней. не имеет корней.Контрольная работа за полугодие. 11 класс. Вариант II Часть 1 При выполнении заданий части 1 в бланке ответов №1 под номером выполняемого вами задания А1– А10 поставьте знак «  » в клеточку, номер которой соответствует номеру выбранного вами ответа. » в клеточку, номер которой соответствует номеру выбранного вами ответа.А1Упростите выражение 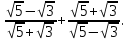 1) 8; 2) 5; 3) 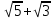 ; 4) ; 4)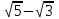 . .А2 Выражение 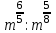 представьте в виде степени с основанием представьте в виде степени с основанием 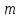 1) 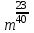 ; 2) ; 2)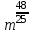 ; 3) ; 3) 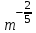 ; 4) ; 4)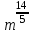 . .А3Вычислите 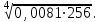 1) 0,0012; 2) 0,12; 3) 0,012; 4) 1,2. А4Найдите множество значений функции 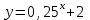 1) 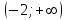 ; 2) ; 2)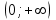 ; 3) ; 3)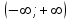 ; 4) ; 4) 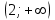 . .А5Найдите все решения уравнения 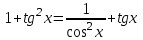 . .1) 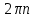 , , 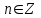 ; 2) ; 2)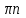 , , 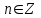 ; ;3) 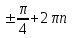 , , 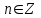 ; 4) ; 4)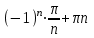 , , 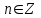 . .А6Для функции 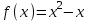 укажите первообразную, график которой проходит через точку М (-3; 0). укажите первообразную, график которой проходит через точку М (-3; 0).1) 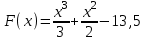 ; 2) ; 2)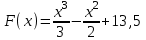 ; ;3) 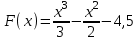 ; 4) ; 4) 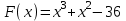 . .А7Найдите производную функции 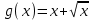 . .1) 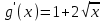 ; 2) ; 2)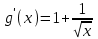 ; ;3) 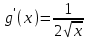 ; 4) ; 4)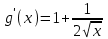 . .А8Определите число целых неотрицательных решений неравенства 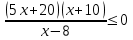 1) 10; 2) 12; 3) 8; 4) 11. А9Укажите промежуток, которому принадлежат корни уравнения 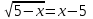 1) 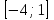 ; 2) ; 2) 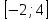 ; 3) ; 3) 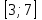 ; 4) ; 4) 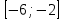 . .А 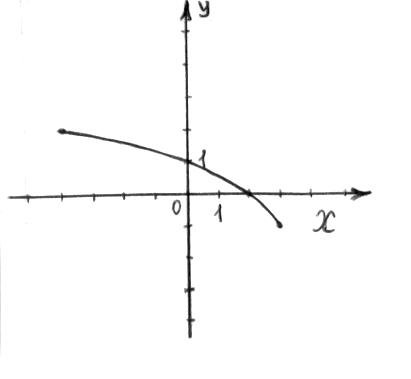 10 Функция задана графиком. Укажите область определения функции. 10 Функция задана графиком. Укажите область определения функции. 1) 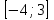 ; 2) ; 2) 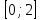 ; ;3) 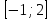 ; 4) ; 4) 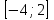 . .Часть 2 Ответом к каждому заданию этой части будет некоторое число. Это число надо вписать в бланк ответов №1 справа от номера задания (В1-В5), начиная с первой клеточки. Каждую цифру или знак минус отрицательного числа пишите в отдельной клеточке строго по образцу из верхней части бланка. Единицы измерений писать не нужно. Если ответ получится в виде дроби, то её надо округлить до ближайшего целого числа. В1Пусть (х0; у0) – решение системы. 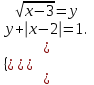 Найдите х0-у0 . В2На рисунке изображён график производной функции 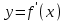 заданной на отрезке заданной на отрезке 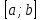 . .Исследуйте функцию 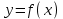 на монотонность на монотонностьи в ответе укажите число промежутков возрастания. 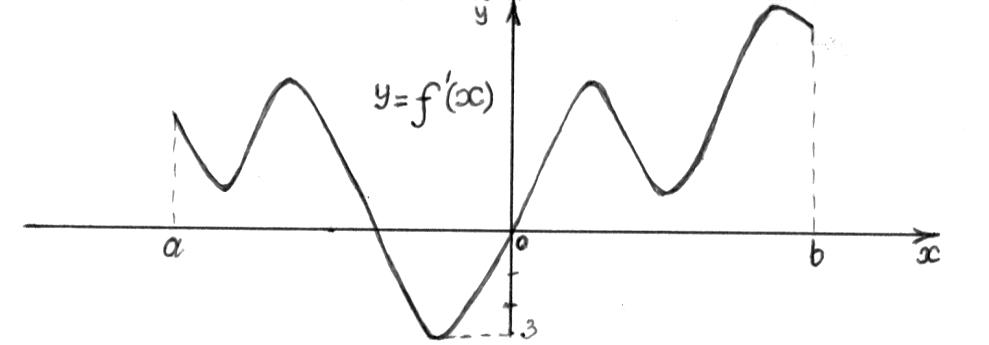 В3 Вычислите: 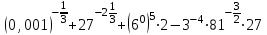 . .В4Найдите число корней уравнения 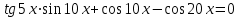 на промежутке на промежутке 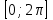 . .В5 Прикаком значении nфункция 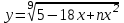 имеет максимум в точке х0 = -3 ? имеет максимум в точке х0 = -3 ?Часть 3 Для записи ответов к заданиям этой части(С1-С3) используйте бланк ответов №2. Запишите сначала номер задания, а затем полное решение. С1Решите уравнение 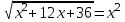 . .С2Решите уравнение 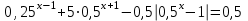 . . С3Найдите все значенияр, при которых уравнение 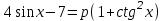 имеет хотя бы один корень. имеет хотя бы один корень.Контрольная работа по теме: Производная и первообразная показательной и логарифмической функций. 11 класс. Вариант I. А1. Найдите производную функции 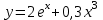 1) 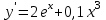 ; ;2) 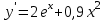 ; ;3) 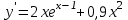 ; ;4) 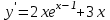 . .А2. На каком из рисунков изображен график производной функции 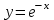 1) 2) 3) 4) 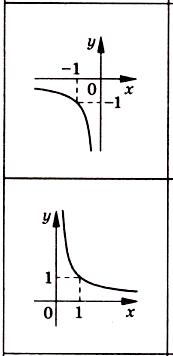 А3. Найдите значение производной функции 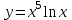 в точке 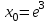 . .1) 15; 2) 15 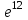 ; 3) 5 ; 3) 5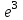 ; 4) 16 ; 4) 16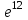 . .А4. Найдите угловой коэффициент касательной, проведённой к графику функции 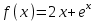 в его точке с абсциссой в его точке с абсциссой 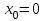 . .1) 1; 2) 2; 3) 3; 4) 0. А5. Касательной к графику функции 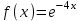 в точке в точке 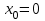 является: 1) 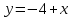 ; 2) ; 2) 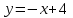 ; 3) ; 3)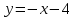 ; 4) ; 4)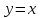 . .В1. Найдите значение С первообразной F функции 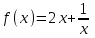 на промежутке (0;  ), если F(1) = 3. ), если F(1) = 3. |
