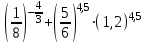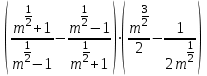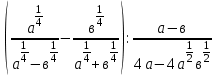|
|
Контрольная работа Определенный интеграл. Контрольная работа 1 по темеПервообразная и интеграл (Е. М. цикл) Цель работы знания таблицы и правил нахождения первообразных
Критерии оценивания
№
задания
|
Характеристика задания
|
Проверяемые элементы
|
Балл за выполнение проверяемого элемента
|
Балл за выполнение задания
|
1
|
Решение логарифмических неравенств
|
Свойство логарифмической функции
|
1
|
3 балла
|
Методы решения
|
1
|
Решение квадратичного неравенства
|
1
|
2
|
Решение неравенства с модулем
|
Определение модуля
|
1
|
4 балла
|
Метод решения
|
2
|
Запись ответа
|
1
|
3
|
Решение уравнения с модулем
|
Определение модуля
|
1
|
4 баллов
|
Метод решения
|
2
|
Запись ответа
|
1
|
4
|
Решение уравнения с параметром
|
Нахождение дискриминанта квадратного уравнения и анализ
|
2
|
5 баллов
|
Решение неравенства
|
2
|
Запись ответа
|
1
|
5
|
Решение системы уравнений
|
Метод решения систем уравнений
|
2
|
7 баллов
|
Определение ОДЗ системы
|
2
|
Методы решения иррациональных уравнений
|
2
|
Запись ответа
|
1
|
Контрольная работа по алгебре и началам анализа в 11 классе(Е.-М. цикл)
Цель работы:
- знания таблицы и правил нахождения первообразных
- проверить умения доказывать является ли функция первообразной для данной;
умения находить первообразную степенной функции;
умения находить первообразную многочлена, элементарных функций;
вычислять интеграл;
вычислять площадь криволинейной трапеции, применяя формулу Ньютона-Лейбница;
Вариант-1 Вариант-2
1.Докажите,что функция F(х) является первообразной для функции f(х) на R:
F(х)=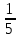 х5-sin2xF(x)= х5-sin2xF(x)=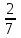 x7-cos2xF(x)=x4-sin2x f(x)=2x6+sin2x x7-cos2xF(x)=x4-sin2x f(x)=2x6+sin2x
2.Для функции
у=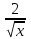 +4xy= +4xy=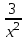 +x2-x +x2-x
найдите первообразную, которая удовлетворяет условию
F(4)=2 F(1)=3
3.Вичислите интегралы:
а) 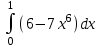 а) а) 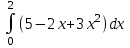
б) 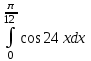 б) б) 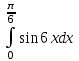
4.Вычислите площадь фигуры, ограниченной линиями:
у=х2 и у=х+2 у=-х2 и у=х-2
5. Найдите сумму абсцисс точек пересечения графиков функции и её первообразной, если одна из этих точек находится на оси ординат.
у = (х – 1)(х + 2)у = (х – 3)(х + 2)
.
Критерии оценивания
|
«5»
|
21- 22 балл
|
«4»
|
16-20 баллов
|
«3»
|
10-15 баллов
|
Распределение заданий по содержанию и уровню сложности
Содержательные линии
|
Воспроиз-ведение знаний
|
Приме-нение знаний
|
Интег-рация
|
% со-отно-шение
|
Первообразная функции
|
№1,№2
|
|
№5
|
60%
|
Формула Ньютона-Лейбница
|
|
№4
|
|
20%
|
Определенныйинтеграл
|
|
№3
|
|
20%
|
Итого
|
40%
|
40%
|
20%
|
100%
|
Спецификация заданий и критерии оценивания
№
|
Характеристика задания
|
Проверяемые элементы
|
Балл за выполнение проверяемого элемента
|
Балл за выполненное задание
|
1
|
Правило вычисления первообразных
|
1)Знание определения первообразной функции
2)Нахождение производной
3)Запись ответа
|
1 балл
1 балл
балл
|
3балла
|
2
|
Нахождение первообразной, график которой проходит через точку.
|
1)Правило вычисления первообразных
|
1 балл
|
4 балла
|
|
2)Нахождение значения С
|
1 балл
|
|
3).Запись ответа
|
1 балл
|
|
4) .Вычисления
|
1 балл
|
3
|
Нахождение определенного интеграла
|
1). Первообразная элементарных функций
|
1 балл
|
5 баллов
|
|
|
2). Первообразная сложной функции
|
2 балл
|
|
|
3). Правило интегрирования
|
1 балл
|
|
|
4). Вычисления
|
1 балл
|
4
|
Нахождение площади фигуры, ограниченной линиями
|
1)Нахождение точек пересечения прямой и параболы
2)Построение графиков
3)Запись формулы для вычисления площади фигуры
4)Нахождение первообразной
5)Применение формулы Ньютона-Лейбница
6)Вычисления
|
1 балл
1 балл
0,5 балла
1 балл
1 балла
0,5 балл
|
5 баллов
|
|
Нахождение точек пересечения графиков функции
|
1).Нахождение первообразной
2).Определение координат точки, лежащей на оси ординат
|
1 балл
1 балл
|
5 балла
|
5
|
3). Составление уравнения для нахождения точек пересечения графиков функции
|
2 балла
|
|
4).запись ответа
|
1 бал
|
Контрольная работа №2
по теме: «Степени и корни. Степенная функция»
Цель работы: прооверить уровень ГОСО
- знания определение корня п-й степени и его свойства
- знания определения арифметического корня п-й степени
знания определения степени с рациональным и иррациональным показателем и их свойства;
умения преобразовыватьрациональные и иррациональные выражения
умения вычислять арифметический корень п-й степении и степень с рациональным показателем
Вариант 1 Вариант 2
1.Вычислите:
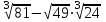 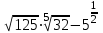
2. Упростите выражение:
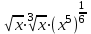 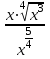
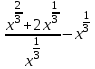 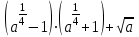
3.Упростите выражение:
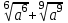 , где а < 0 , где а < 0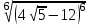
4.Вычислите:
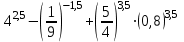 91,5 - 91,5 - 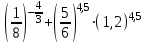
5.Найдите значение выражения при
m = - 5а = 16, в = 9
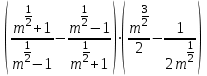 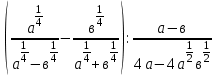
Критерии оценивания
|
«5»
|
21- 22 балл
|
«4»
|
16-20 баллов
|
«3»
|
10-15 баллов
|
Распределение заданий по содержанию и уровню сложности
Содержательные линии
|
Воспроиз-ведение знаний
|
Приме-нение знаний
|
Интег-рация
|
% со-отно-шение
|
Арифметический корень п-й степени, степень с рациональным показателем
|
№1,№2
|
|
|
40%
|
Свойства степени с рациональным показателем
|
|
№4
|
№5
|
40%
|
Иррациональные выражения
|
|
№3
|
|
20%
|
Итого
|
40%
|
40%
|
20%
|
100%
|
Спецификация заданий и критерии оценивания
№
|
Характеристика задания
|
Проверяемые элементы
|
Балл за выполнение проверяемого элемента
|
Балл за выполненное задание
|
1
|
Нахождение значения иррационального выражения
|
1)Нахождениеарифметического корня п-й степени
|
балл
|
3 балла
|
|
2)Умножение степеней
|
1 балл
|
|
3)Запись ответа
|
1 балл
|
2
|
Преобразование выражения ,содержащего арифметический корень п-й степени, степень с рациональным показателем
|
1)Преобразование корня в степень с рациональным показателем
|
1 балл
|
4 балла
|
|
2)Умножение , деление степеней
|
1 балл
|
|
3).Разложение на множители, сокращение дроби
|
1 балл
|
|
4) .Раскрытие скобок с применением ФСУ
|
1 балл
|
3
|
Упрощение иррационального выражения
|
1). Нахождениеарифметического корня п-й степени.используя свойства
|
2 балл
|
5 баллов
|
|
2).Исследование подкоренного выражения
|
2 балл
|
|
3). Запись ответа
|
1 балл
|
4
|
Нахождение числового значения выражения
|
1).Умножение степеней с одинаковыми показателями
|
2 балл
|
5 баллов
|
|
|
2).Преобразование степени в корень п-й степени
|
2 балл
|
|
|
3).Вычисление корня п-й степени
|
1 балл
|
5
|
Упрощение буквенного выражения , содержащего степени с рациональным показателем
|
1).Преобразование алгебраических дробей, содержащих степени с рациональным показателем
|
3балл
|
5 балла
|
|
2). Вычисление значения степени с рациональным показателем
|
2 балл
|
|
|
|
 Скачать 0.81 Mb.
Скачать 0.81 Mb. х5-sin2xF(x)=
х5-sin2xF(x)=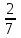 x7-cos2xF(x)=x4-sin2x f(x)=2x6+sin2x
x7-cos2xF(x)=x4-sin2x f(x)=2x6+sin2x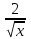 +4xy=
+4xy=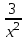 +x2-x
+x2-x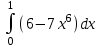 а)
а) 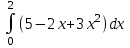
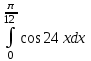 б)
б) 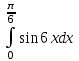
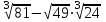
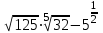
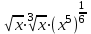
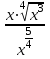
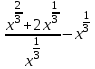
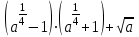
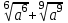 , где а < 0
, где а < 0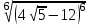
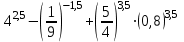 91,5 -
91,5 -