Контрольная работа 3 Линия тождественных преобразований. Тождественные преобразования алгебраических выражений Задания
 Скачать 75.39 Kb. Скачать 75.39 Kb.
|
|
3.Упростите выражение: а) (5х + 2)2 – 40х б) 27х2 – 3(3х – 1)2 Материал для итогового контроля результатов работы над темой Запишите в виде многочлена стандартного вида: а) (1/2 а2 – 8b)2; б) (3а + 2b)(9а2 – 12ab + 4b2). Разложите на множители многочлен: а) 36х2+84х+49; б) –х4 + 8х2 – 16. Решите уравнение (3x – 2)2 = (2x – 1)2 + 5х2 +11. Докажите неравенство 16х2 + 25у2 >40ху – 20. Докажите, что значение выражения 1192 +2*119*112+1122кратно 231. Разложите на множители многочлен х2n + 6хnyk + 9у2k. Разработайте методику работы с теоремой о разложении квадратного трехчлена, имеющего действительные корни, на множители. Комментарий: при выполнении задания: определите, какой способ разложения на множители лежит в основе доказательства теоремы; предложите вариант, как «навести» учащихся на использование теоремы Виета в процессе доказательства рассматриваемой теоремы; приведите примеры задач, которые могут использоваться на этапе мотивации введения теоремы, предложите вариант работы с этими задачами; разработайте фрагмент урока: доказательство теоремы о разложении квадратного трехчлена на множители. Способ разложения на множители, лежащий в основе доказательства теоремы: вынесение общего множителя за скобки; способ группировки. Примеры задач, которые могут использоваться на этапе мотивации введения теоремы, предложите вариант работы с этими задачами: Найдите корни уравнения без использования формулы для нахождения корней квадратного уравнения: 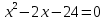 Попробуем сгруппировать: 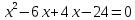 Вынесем общие множители за скобки: 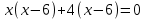 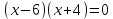 Произведение равно нулю, когда хотя бы один из множителей равен нулю. 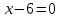 или или 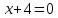 . .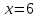 или или 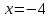 . .Однако не всегда удается с первого раза правильно сгруппировать слагаемые,чтобы вынести общий множитель и найти корни. Например: 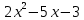 . . В этом нам поможет разложение квадратного трехчлена на множители. Доказательство: 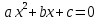 Какой коэффициент мы можем вынести за скобки, чтобы получить приведенное квадратное уравнение? 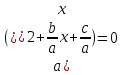 Пусть 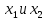 – решения уравнения. Тогда по теореме Виета – решения уравнения. Тогда по теореме Виета 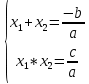 Следовательно, 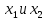 – корни квадратного уравнения. Значит, при подстановке в исходное уравнение превращается в верное равенство. – корни квадратного уравнения. Значит, при подстановке в исходное уравнение превращается в верное равенство.Произведение равно нулю, когда один из множителей равен нулю. Попробуем представить исходное уравнение через произведение корней: Так как 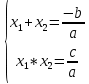 , получим , получим 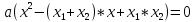 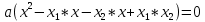 Сгруппируем: 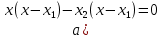 Вынесем общий множитель за скобки: 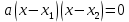 Получили разложение квадратного трехчлена на множители Линия тождественных преобразований. Тождественные преобразования трансцендентных выражений Задания К какому виду математических выражений относятся тригонометрические выражения? Логарифмические выражения? Тригонометрические и логарифмические выражения относятся к трансцендентным. Углом какой четверти является угол α, если а) 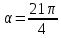 ; б) ; б)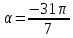 ; в) ; в) 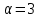 ; г) ; г) 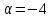 ? ?а) 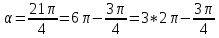 – III четверть; – III четверть;б) 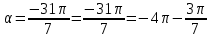 – IV четверть; – IV четверть;в) 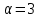 ; ; 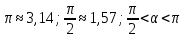 – II четверть; – II четверть;г) 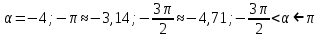 – II четверть. – II четверть.Определите знак произведения: 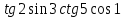 . .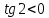 – II четверть. – II четверть.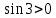 – II четверть. – II четверть.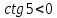 – IV четверть. – IV четверть.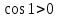 – I четверть. – I четверть.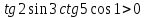 . .Какой знак имеет произведение 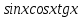 при: а) при: а) 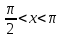 ; б) ; б)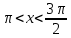 ? ?а) 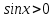 ; ; 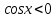 ; ; 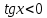 ; ; 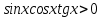 . .б) 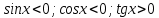 ; ;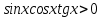 . .Существует ли такое значение х, при котором выполняется равенство 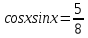 ? ?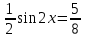 ; ;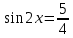 ; ; 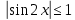 Ответ: не существует. Упростите выражение: а) 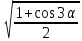 ; б) ; б) 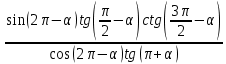 . .а) 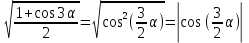 ; ; б) 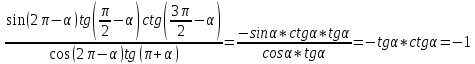 . .Вычислите: а) 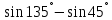 ; б) ; б)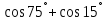 . .а) 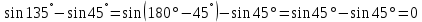 ; ; б) 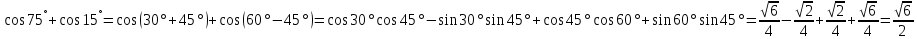 . .Известно, что 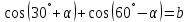 . Найдите . Найдите 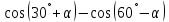 . .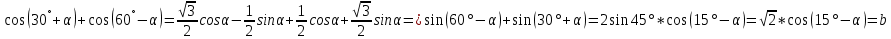 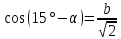 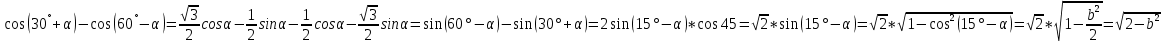 . .Проанализируйте по учебникам разных авторских коллективов (например, Мордкович А.Г. «Алгебра 10 класс» и Муравин Г.К., Муравина О.В. «Алгебра и начала анализа 10 класс») содержание темы «Тригонометрические функции. Преобразование тригонометрических выражений». Комментарий: при выполнении задания ориентируйтесь на последовательность следующих действий: выделите основные и сопутствующие понятия; составьте тематическое планирование изучения темы (всей темы); выделите обязательные результаты обучения по теме (преобразования); сформулируйте цель и задачи обучения этой теме (преобразования): образовательные, развивающие, воспитательные. Основные и сопутствующие понятия. Мордкович А.Г. «Алгебра 10 класс» Тригонометрическая окружность Числовая окружность, Четверти единичной окружности Открытая дуга Ядро аналитической записи дуги Аналитическая запись дуги Синус числа а Косинус числа а Тангенс числа а Котангенс числа а Тригонометрическая функция числового аргумента а Синус угла альфа Косинус угла альфа Угол в 1о Угол в 1 радиан Закон (уравнение) гармонических колебаний Синусоида Тангенсоида Главная ветвь тангенсоиды Арксинус а Арккосинус а Арктангенс а Арккотангенс а Формулы синуса и косинуса суммы аргументов Формулы синуса и косинуса разности аргументов Теорема сложения Формула тангенса суммы аргументов Формулы приведения Формулы двойного аргумента Формулы понижения степени, формулы половинного аргумента Преобразование сумм тригонометрических функций в произведения Преобразование произведений тригонометрических функций в суммы Преобразование выражения Asinx+Bcosx к виду Сsin(x+t) Муравин Г.К., Муравина О.В. «Алгебра и начала анализа 10 класс» Угол поворота Угол в 1 радиан Синус угла Косинус угла Единичная окружность Синус угла 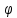 Косинус угла 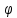 Функции переменной 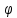 Тангенс угла Ось тангенсов Угол наклона прямой Котангенс угла Синусоида Косинусоида Тангенсоида Котангенсоида Зависимости между тригонометрическими функциями одного и того же аргумента Формула косинуса суммы Формула косинуса разности Формула синуса суммы Формула синуса разности Формула тангенса суммы Формула тангенса разности Формула тангенса двойного угла Формула перехода от произведения косинусов к их сумме Формула перехода от суммы/разности косинусов к их произведению Формула перехода от суммы/разности синусов к их произведению Однородное уравнение второй степени Тематическое планирование изучения темы Тематическое планирование:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
