Контрольная работа 3 Линия тождественных преобразований. Тождественные преобразования алгебраических выражений Задания

• Название: Контрольная работа 3 Линия тождественных преобразований. Тождественные преобразования алгебраических выражений Задания
• Дата: 12.11.2022
• Размер: 75.39 Kb.
• Имя файла: 3.docx
• Тип: Контрольная работа; #784750
• страница: 3 из 3

Типы уроков:

Комбинированный - К

Урок-объяснение нового материала - УОНМ

Обобщающий урок - ОУ

Урок-лекция -УЛ

Урок-зачет - УЗ

Контроль знаний - КЗ

Отработка навыков/закрепление знаний и навыков - ОЗУН

Урок-практикум - УП

Обязательные результаты обучения по теме (преобразования);

В результате изучения тригонометрии ученик должен знать:

• 
  основные тригонометрические тождества для синуса и косинуса, для тангенса и котангенса
  
• 
  значения 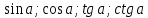некоторых острых углов
  
• 
  формулы суммы и разности двух углов
  
• 
  формулы двойного угла
  
• 
  формулы половинного угла
  
• 
  формулы преобразования суммы тригонометрических функций в произведение и произведения в сумму
  
• 
  формулы универсальной подстановки (через tg a/2)
  
• 
  формулы приведения
  
• 
  формулы для решения простейших тригонометрических уравнений
  
• 
  обратные тригонометрические функции, их графики и свойства (арксинус, арккосинус, арктангенс, арккотангенс)
  
• 
  решение тригонометрических неравенств
  

уметь:

• 
  выполнять преобразования выражений с помощью тригонометрических тождеств и формул
  
• 
  решать тригонометрические уравнения и неравенства
  
• 
  пользоваться формулами приведения для вычисления значений тригонометрических выражений
  
• 
  использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: практических расчетов по формулам, используя при необходимости справочные материалы и простейшие вычислительные устройства.
  

Цель и задачи обучения этой теме (преобразования): образовательные, развивающие, воспитательные.

Цель:

Создать условия для понимания обучающимися необходимости знаний тригонометрических преобразований для дальнейшего изучения курса математики и решения задач, уравнений и неравенств.

Задачи:

Образовательные:

• 
  способствовать овладению языком тригонометрии в устной и письменной форме, необходимыми знаниями и умениями, интеллектуальному развитию учащихся;
  
• 
  сформировать представления о тригонометрии как языке науки;
  
• 
  объяснить значимость тригонометрии для научно-технического прогресса;
  
• 
  формировать навыки применения свойств тригонометрических функций;
  
• 
  способствовать совершенствованию и развитию важнейших математических знаний и умений.
  

Развивающие:

• 
  развить логическое мышление, алгоритмическую культуру, способности учащихся к математической деятельности;
  
• 
  развивать точную, информативную речь.
  

Воспитательные:

• 
  содействовать воспитанию интереса к математике, воспитывать активность, мобильность, умение общаться, общую культуру;
  
• 
  способствовать повышению уровня самостоятельности учащихся при работе с учебным материалом, формировать умение обосновывать свою точку зрения.
  

10. 
    Разработайте методику введения понятия «логарифм».
    

Комментарий: при выполнении задания ориентируйтесь на последовательность следующих действий:

• 
  выберите один из вариантов изучения темы (место по одному из учебников);
  
• 
  выделите знания и умения, на которые необходимо опираться при введении понятия «логарифм»;
  
• 
  предложите задания для актуализации необходимых знаний и умений;
  
• 
  разработайте набор задач для первичного закрепления;
  
• 
  разработайте фрагмент урока по введению понятия «логарифм числа».
  

Учебник «Алгебра 11 класс»(Мордкович, Семенов) часть 1.

Понятие логарифма вводится для обдумывания ситуации с показательным уравнением. А именно: показательное уравнение решается графически, и по чертежу мы не можем определить значение некоторого числа, поэтому нужно вводить новый символ.



Знания и умения, на которые необходимо опираться при введении понятия «логарифм»: знание определений показательной функции, показателя степени, основания, свойств показательной функции; умение графически строить и решать показательные уравнения и неравенства.

Задания для актуализации необходимых знаний и умений.

Выполните задания:

1. 
   Изобразите график функции у=2x² и найдите х при у=8.
   

Решите уравнения:

2. 
   3^х=81
   
3. 
   5^2х=2^3х 
   
4. 
   3^x+3^x+2=30
   

Набор задач для первичного закрепления

1. 
   Найдите решения уравнений:
   

3^x=5

10^x=0,7

(1/3)^x=3

2. 
   Подставьте числа в уравнение таким образом, чтобы получилось верное равенство:
   

2, 4, 16 log( )( )=( ), т.к ( )( )=( )	log(4)(16)=(2), т.к (4)(2)=(16) ИЛИ log(2)(16)=(4), т.к (2)(4)=(16)
-2, 1/9, 3 log( )( )=( ), т.к ( )( )=( )	log(3)(1/9)=(-2), т.к (3)(-2)=(1/9)
1/2 , 3, 1/8 log( )( )=( ), т.к ( )( )=( )	log(1/2)(1/8)=(3), т.к (1/2)(3)=(1/8)
-4, 625, 1/5 log( )( )=( ), т.к ( )( )=( )	log(1/5)(625)=(-4), т.к (1/5)(-4)=(625)
-5, 2, 25 log( )( )=( ), т.к ( )( )=( )	Нет решения, так как основание должно быть больше 0 и не равно 1. -5 меньше 0.
64, 1/2, 8 log( )( )=( ), т.к ( )( )=( )	log(64)(8)=(1/2), т.к (64)(1/2)=(8)
2, 7, -49 log( )( )=( ), т.к ( )( )=( )	Нет решения, так как число под знаком логарифма должно быть положительным.
1/5, 1/2, 1/25 log( )( )=( ), т.к ( )( )=( )	log(1/25)(1/5)=(1/2), т.к (1/25)(1/2)=(1/5)

Фрагмент урока по введению понятия «логарифм числа».

Выполните задания:

1. 
   Изобразите график функции у=2x² и найдите значения х при у=8.
   

Решите уравнения:

2. 
   3^х=81
   
3. 
   5^2х=2^3х 
   
4. 
   3^x+3^x+2=30
   
5. 
   2^x=6
   

Решая последнее показательное уравнение, возникает вопрос: как найти корень и записать ответ.

Решим уравнение 2^x=6 графически. Каков алгоритм решения уравнения этим методом?

Видим, что уравнение имеет единственный корень.

Возникла трудность: по чертежу мы не можем определить значения корня, можем только установить, что это число, заключенное в промежутке от 2до3.

При решении уравнения 2^x=6, для записи единственного решения введем новый символ – log₂(у), предполагая, что 2^х=у. При у=6 x=log₂6.Теперь для любого уравнения вида 2^x=b, где b>0 (Объясните, почему?) можно записать общее решение x=log₂b.

Аналогично рассуждая, мы найдем решения и этих уравнений:3^x=5 10^x=0,7 (1/3)^x=3 (x=log₃5; x=log₁₀0,7; x=log_1/33).

Единственный корень уравнения вида a^x=b , где а>0, a≠1 и b>0 математики договорились записывать x=log_ab.

Логарифмом положительного числа b по положительному и отличному от единицы основанию a называют показатель степени, в которую надо возвести а, чтобы получилось число b.

Выделим существенные признаки числа log_ab: Основание а: a>0, a≠1. Число под знаком логарифма: b>0.

Операция вычисления логарифма (нахождения значения логарифма) – логарифмирование. Обратная операция – возведение в степень.