 4.2 Текст программы расчета исследуемых параметров.
Программа написана на языке программирования Pascal ABC.
Programmatmodel
uses crt; оператор открытия консоли для вывода результата
Var q0,qi,q1,q2,h,t,Tmax,C,g,m,Mk,Mg:real; оператор задания переменной
F:text; оператор типа файла F
begin
clrscr; оператор очистки экрана
writeln('BBOD C '); оператор вывода данных
readln(C); оператор ввода данных
assign(F,' C:\ matmodel.txt'); оператор привязывания переменной к файлу
rewrite(F); оператор открытия файла для записи переменной F
 h:=0.01;
Mk:=13000;
Tmax:=2.1;
g:=9.8;
Mg:=10900;
t:=0; блок расчетов
M:=Mk+Mg
q0:=(M*g)/(2*C);
M:=Mk;
q1:=q0;
qi:=q0;
Repeat оператор цикла
q2:= 2*qi - q1 + sqr(h)*(g-(2*C*qi)/M);
Writeln(q2:0:5,t:15:4); оператор вывода переменной
Writeln(F,q2:0:5,t:15:4); оператор вывода переменной
  q1:=qi;
qi:=q2; блок расчетов
t:=t + h;
Until t>=Tmax; оператор условия
Readln; оператор ввода переменной
End.
 5 Анализ результатов математического моделирования 5.1 Графики собственных колебаний
Шаг разностной аппроксимации h берем равным 0,01, время интегрирования 2,1 секунды.
По составленной программе произведем расчеты для различной жесткости рессорного подвешивания. Результаты расчета занесем в таблицу (Приложение А), и по этим результатам построим графики зависимостей перемещений от времени.
 Рисунок 5 – График собственных колебаний подпрыгивания
при С1=6120 кН/м
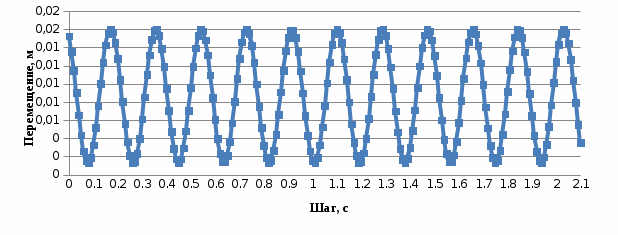 Рисунок 6 – График собственных колебаний подпрыгивания
 при С2=7350 кН/м
 
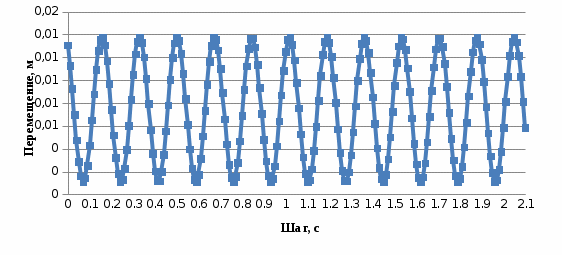
Рисунок 7 – График собственных колебаний подпрыгивания
при С3=8570 кН/м
процесс кузова
Параметрами, характеризующими колебания кузова вагона на пружинах рессорного подвешивания, являются амплитуда А, период колебаний Т и частота колебаний ν.
Значения периода и амплитуды колебаний возьмем с графиков и таблицы (приложение А), приведенных на рисунках 5 – 7. Определенные по графикам и таблице (приложение А) параметры А и Т и рассчитанные значения ν приведены в таблице 3.
Формула для определения частоты колебаний ν, Гц, имеет вид 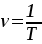(23):
 (23)
Таблица 3 – Параметры собственных колебаний кузова вагона.
Жесткость рессорного подвешива-ния кН/м
|
Параметры колебаний
|
Погреш-ность
|
Расчетные значения
|
Амплиту-да А, м
|
Пери-од Т, с
|
Часто-та v, Гц
|
q, %
|
v, %
|
q, м
|
v, Гц
|
6120
|
0,01831
|
0,20
|
5,00
|
4,29
|
-2,46
|
0,01913
|
4,88
|
7350
|
0,01525
|
0,19
|
5,26
|
4,27
|
1,62
|
0,01593
|
5,35
|
8570
|
0,01308
|
0,17
|
5,88
|
4,25
|
-1,77
|
0,01366
|
5,78
|
Окончание таблицы 3
Таким образом, подсчитали погрешность каждой частоты колебаний и начальных перемещений при различной массе груза в вагоне. Полученная погрешность не превышает допустимой, которая равна 5%. Можно сделать вывод, что математическая модель и алгоритм решения задачи разработаны верно.
|
Скачать 469.08 Kb.