Математическая модель в динамике твердых тел представляет собой систему, состоящую из уравнения движения и начальных условий. Для получения уравнения движения математической модели собственных колебаний подпрыгивания кузова вагона на пружинах рессорного комплекта воспользуемся принципом Д’Аламбера. Согласно этого принципа, вырежем твердое тело (кузов вагона), действие отброшенных связей заменим реакциями упругих элементов, приложим к нему все внешние силы и силы инерции в центре масс. Сила инерции направлена в сторону, противоположную направлению q. Расчетная схема показана на рисунке 3.
 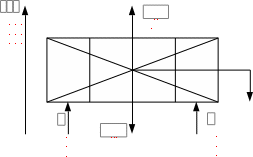
где 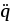 – ускорение перемещения кузова; – ускорение перемещения кузова;
R– реакции рессорного подвешивания.
Рисунок 3 – Расчетная схема
Спроецируем все силы, приложенные к телу, на выбранную ось движения, и получим уравнение движения – уравнения свободных собственных колебаний:
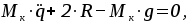 (6) (6)
где 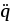 – ускорение перемещения кузова, м/с2; – ускорение перемещения кузова, м/с2;
R – реакция рессорного подвешивания, 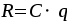 , Н. , Н.
Ноль в правой части обозначает, что в процессе колебаний на тело не действует ни каких сил, т.е. колебания являются собственными (свободными), что соответствует условию задачи.
Уравнение (5) с учетом 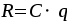 будет иметь вид: будет иметь вид:
 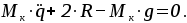 (7) (7)
Так как данное уравнение по смыслу относится к задачам Коши
(задачам с начальными условиями), то математическая модель должна содержать начальные условия. Разместим в кузове вагона груз массой 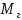 . Центр тяжести кузова переместится на величину . Центр тяжести кузова переместится на величину  . Общая масса кузова и груза будет равна сумме . Общая масса кузова и груза будет равна сумме 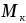 и и 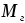 . .
Для данного случая уравнение будет иметь вид:
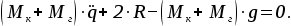 (8) (8)
Так как после установки груза в кузов тело находится в состоянии покоя (отсутствуют перемещения), то 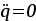 , то из уравнения (8) получим: , то из уравнения (8) получим:
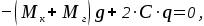
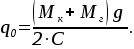 (9) (9)
Запишем математическую модель собственных колебаний подпрыгивания кузова вагона на пружинах рессорного комплекта, система:
 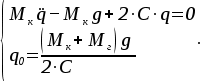 (10) (10)
Определим начальное перемещение  кузова вагона для кузова вагона для 
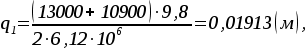
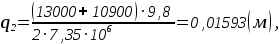
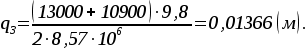
 3 Выбор метода решения математической модели 3 Выбор метода решения математической модели
3.1 Анализ методов решения ОДУ
Для решения ОДУ существует множество методов. Одними из наиболее распространенных методов вляются: метод Милна, метод Адамса, Рунге-Кутта, Эйлера-Коши, разностный метод.
Метод Рунге-Кутта обладают следующими отличительными свойствами:
- этот метод является одноступенчатым: чтобы найти ym=1, нужна информация только о предыдущей точке xm, ym.
- согласуется с рядом Тейлора вплоть до членов порядка hp, где степень р различна для различных методов и называется порядком метода.
- не требует вычисления производных от f(x,y), а требует только вычисления самой функции.
Именно благодаря третьему свойству метод Рунге-Кутта более удобен для практических вычислений, нежели ряд Тейлора. Однако, как и можно ожидать, для вычисления одной последующей точки решения придется вычислять функцию f(x,y) несколько раз при различных значениях x и y. Этот метод требует большей квалификации и времени на отладку.
Широко распространенным семейством многошаговых методов является метод Адамса. В практических расчетах чаще всего используется вариант метода Адамса, имеющий четвертый порядок точности и использующий на каждом шаге результаты предыдущих четырех. Сравнивая метод Адамса с методом Рунге-Кутта той же точности, отмечаем его экономичность, поскольку он требует вычисления лишь одного значения правой части на каждом шаге.
 Но метод Адамса неудобен тем, что невозможно начать счет по одному лишь неизвестному значению. Расчет может быть начат лишь с узла. Но метод Адамса неудобен тем, что невозможно начать счет по одному лишь неизвестному значению. Расчет может быть начат лишь с узла.
Значения необходимые длявычисления, нужно получить каким-либо другим способом, что существенно усложняет алгоритм. Кроме того, метод Адамса не позволяет изменить шаг в процессе счета, этого недостатка лишены одношаговые методы.
Итерационный метод Эйлера-Коши применим для интегрирования дифференциальных уравнений любого порядка.
Если имеем дифференциальное уравнение (11):
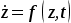 . (11) . (11)
с начальными условиями (12):
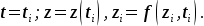 (12) (12)
то формула для интегрирования получается из следующих соображений.
Находят значения функции в виде трех членов разложения ряда Тейлора (13):
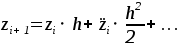 (13) (13)
Затем вторая производная представляется в виде разностного выражения (14):
 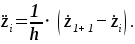 (14) (14)
Подставив выражения (13) уравнение (12), получим:
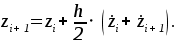 (15) (15)
В выражении (15) значение 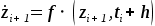 неизвестно, поэтому, чтобы воспользоваться формулой (14), строятся итерационный процесс. неизвестно, поэтому, чтобы воспользоваться формулой (14), строятся итерационный процесс.
Таким образом, циклическая процедура вычислений по формуле (15) представляет итерационный метод Эйлера-Коши для дифференциального уравнения (15).
Метод Милна – конечно-разностный метод решения задачи Коши для системы обыкновенных дифференциальных уравнений 1-го порядка: y/=f(x,y), y(a)=b.
В методе Милна используется конечноразностная формула. Где для вычисления по этой формуле необходимо каким-либо иным способом найти дополнительное начальное значение. Метод Милна имеет 2-й порядок точности, устойчив по Далквисту т.е. все решения однородного разностного уравнения ограничены равномерно. Для устойчивости достаточно, чтобы простые корни характеристичного многочлена левой части разностного уравнения не превосходили по модулю единицы, а кратные – были по модулю строго меньше единицы. В данном случае характеристичный многочлен имеет корни и, следовательно, удовлетворяет указанному условию устойчивости.
 Однако при решении систем уравнений с матрицей А, имеющей отрицательные собственные значения, происходит быстрый рост вычислительной погрешности. Однако при решении систем уравнений с матрицей А, имеющей отрицательные собственные значения, происходит быстрый рост вычислительной погрешности.
Разностный метод интегрирования ОДУ – это метод основанный на замене производной в дифференциальных уравнениях их приближенными разностными аналогами. Для решения будем использовать разностный метод, который имеет преимущества:
- эффективный алгоритм решения;
- легкий для понимания физической сущности алгоритм;
- листинг программы короткий, а следовательно и количество ошибок минимально.
Критерием выбора является условие, когда разность значений двух решений не превышает 5%.
Сущность разностного метода заключается в замене всех производных в уравнении движения их разностными аналогами.
|
 Скачать 469.08 Kb.
Скачать 469.08 Kb.



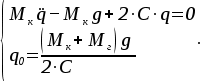 (10)
(10)
 3 Выбор метода решения математической модели
3 Выбор метода решения математической модели Но метод Адамса неудобен тем, что невозможно начать счет по одному лишь неизвестному значению. Расчет может быть начат лишь с узла.
Но метод Адамса неудобен тем, что невозможно начать счет по одному лишь неизвестному значению. Расчет может быть начат лишь с узла. 
 Однако при решении систем уравнений с матрицей А, имеющей отрицательные собственные значения, происходит быстрый рост вычислительной погрешности.
Однако при решении систем уравнений с матрицей А, имеющей отрицательные собственные значения, происходит быстрый рост вычислительной погрешности.