Моделирование собственных колебаний кузова подвижного состава на рессорном подвешивании. КР. Контрольная работа по дисциплине Математическое моделирование систем и процессов Проверил

• Название: Контрольная работа по дисциплине Математическое моделирование систем и процессов Проверил
• Анкор: Моделирование собственных колебаний кузова подвижного состава на рессорном подвешивании
• Дата: 26.03.2022
• Размер: 469.08 Kb.
• Имя файла: КР.odt
• Тип: Контрольная работа; #418078
• страница: 7 из 9

5.3 Оценка влияния жесткости рессорного подвешивания на параметры колебательного процесса

На основании полученных данных параметров таблицы 3, построим график зависимости параметров колебательного процесса от жесткости рессорного подвешивания.

На рисунке 8, 9 приведены графики зависимости.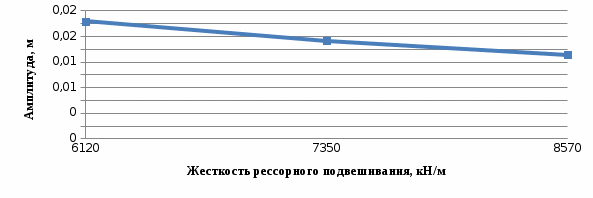



Рисунок 8– График зависимости амплитуды колебаний от жесткости рессорного подвешивания.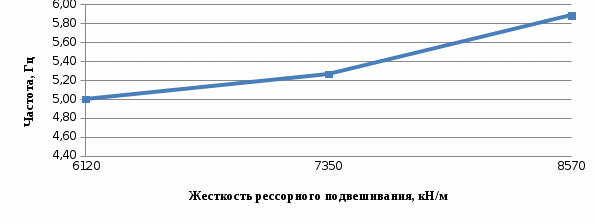



Рисунок 9 – График зависимости частоты колебаний от жесткости рессорного подвешивания..

При увеличении жесткости рессорного подвешивания амплитуда колебаний уменьшается, а частота колебаний увеличивается.

ЗАКЛЮЧЕНИЕ

В ходе данной контрольной работы были описаны особенности конструкции вагона-цистерны модели 15-1487, а также представлено описание технических характеристик тележки модели 18-578, которая подкатывается под данную единицу подвижного состава. Проведен анализ параметров, влияющих на колебания подпрыгивание кузова вагона. Установлено, что на колебательный процесс влияет жесткость рессорного подвешивания.

На основе принципа Даламбера была выбрана расчетная схема, и разработана математическая модель собственных колебаний подпрыгивания кузова вагона на рессорном подвешивании. Математическая модель состоит из уравнения движения и начальных условий.

Выполнен анализ методов решения обыкновенных дифференциальных уравнений. Из этого можно сделать вывод, что разработанная математическая модель может быть решена при помощи разностного метода, путем замены производных в дифференциальных уравнениях их разностными аналогами.

Для решения данной математической модели была составлена блок-схема и приведена программа, написанная на языке PascalABC.

По результатам программы, приведенных в таблице 4 (Приложение А) был построен график зависимости амплитуды колебаний от времени. По этому графику был определен период собственных колебаний вагона на рессорном подвешивании и была вычислена частота колебаний, а также была проведена оценку адекватности математической модели по частоте. Было установлено, что при увеличении жесткости рессорного подвешивания амплитуда колебаний уменьшается, а частота колебаний увеличивается.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1 Конструирование и расчет вагонов: Учебник для вузов ж.-д. трансп./ В.В.Лукин, Л.А. Шадур, В.Н. Котуранов, А.А. Хохлов, П.С. Анисимов; Под ред. В.В. Лукина. М.: УМК МПС России, 2000, 731 с.

2 Соколов М. М., Хусидов В. Д., Минкин Ю. Г. Динамическая нагруженность вагона. М.: Транспорт, 1981. – 207 с.

3 Грузовые вагоны колеи 1520 мм железных дорог. – М.: Транспорт, 1982. – 111 с.

4 Динамика вагона. Вершинский С.В., Данилов В.Н., Челнов И.И.: Учебник для вузов ж. д. транспорта. Изд. 2-е, перераб. – М.:Транспорт, 1978. – 352 с.

5 Вагоны и вагонное хозяйство: Методическое руководство к дипломному проектированию для студентов специальности 190302 – Вагоны / Л.В. Егорова, В.Ф. Лапшин, М.В. Орлов и др.; Под общ. ред. проф. М.В. Орлова. – Екатеринбург: Изд-во УрГУПСа, 2005. – 120 с.

6. Моделирование собственных колебаний кузова вагона на рессорном подвешивании: метод. указания/ Лапшин В.Ф., Архипова Ю.Ю. – Екатеринбург: Изд-во УрГУПС, 2014. – 21 с. "

7 Описание критериев Далквиста https://studopedia.net/13_63295_vibor-metodaresheniya-matematicheskoy-modeli.html. Устойчивость по Далквисту. Строгая и слабая устойчивость. Простейшие примеры. Первый барьер Далквиста ([7, с. 346-351]) URL: https://icmmg.nsc.ru/sites/default/files/pubs/bookodu2_2017.pdf

ПРИЛОЖЕНИЕ А

Таблица 4 – Результаты математического моделирования

Шаг, м	Жесткость рессорного подвешивания кН/м,
	6120	7350	8570
0	0,01831	0,01525	0,01308
0,01	0,01675	0,01356	0,01131
0,02	0,01459	0,01146	0,00926
0,03	0,01203	0,00904	0,00698
0,04	0,00932	0,00658	0,00475
0,05	0,00671	0,00435	0,00288
0,06	0,00446	0,00261	0,0016
0,07	0,00276	0,00156	0,0011
0,08	0,00178	0,00131	0,00143
0,09	0,00162	0,00189	0,00255
0,1	0,00228	0,00324	0,00432
0,11	0,00371	0,0052	0,0065
0,12	0,00577	0,00756	0,0088
0,13	0,00826	0,01004	0,01092
0,14	0,01096	0,01236	0,01258
0,15	0,01361	0,01427	0,01356
0,16	0,01595	0,01554	0,01373
0,17	0,01778	0,01603	0,01308
0,18	0,01891	0,0157	0,01168
0,19	0,01924	0,01457	0,00972
0,2	0,01873	0,01277	0,00746
0,21	0,01745	0,0105	0,00519
0,22	0,0155	0,00803	0,00322
0,23	0,01307	0,00563	0,00181
0,24	0,01039	0,00358	0,00114
0,25	0,00772	0,0021	0,00129
0,26	0,00529	0,00136	0,00226
0,27	0,00335	0,00145	0,00391
0,28	0,00207	0,00235	0,00602
0,29	0,00158	0,00397	0,00832
0,3	0,00192	0,00612	0,0105
0,31	0,00306	0,00856	0,01228
0,32	0,00489	0,01101	0,01342
0,33	0,00724	0,01319	0,01377
0,34	0,00988	0,01487	0,01328
0,35	0,01258	0,01584	0,01202
0,36	0,01508	0,016	0,01016
0,37	0,01713	0,01533	0,00794
0,38	0,01855	0,01391	0,00565
0,39	0,0192	0,01189	0,00359
0,4	0,01903	0,00952	0,00205
0,41	0,01805	0,00704	0,00121
0,42	0,01634	0,00475	0,00119
0,43	0,01408	0,0029	0,002
0,44	0,01147	0,0017	0,00352
0,45	0,00876	0,0013	0,00556
0,46	0,00621	0,00172	0,00784
0,47	0,00405	0,00293	0,01008
0,48	0,00249	0,00479	0,01196
0,49	0,00168	0,00709	0,01324
0,5	0,00169	0,00956	0,01376
0,51	0,00252	0,01194	0,01345
0,52	0,00409	0,01394	0,01234
0,53	0,00626	0,01535	0,01059
0,54	0,00882	0,016	0,00841
0,55	0,01152	0,01583	0,00611
0,56	0,01413	0,01484	0,00399
0,57	0,01638	0,01316	0,00232
0,58	0,01807	0,01096	0,00132
0,59	0,01904	0,00851	0,00113
0,6	0,0192	0,00608	0,00177
0,61	0,01853	0,00394	0,00315
0,62	0,01709	0,00233	0,00511
0,63	0,01503	0,00144	0,00736
0,64	0,01253	0,00137	0,00963
0,65	0,00983	0,00212	0,01161
0,66	0,00718	0,00361	0,01304
0,67	0,00484	0,00568	0,01372
0,68	0,00303	0,00808	0,01358
0,69	0,0019	0,01055	0,01263