Контрольная работа по дисциплине Теория автоматического управления Задание 1
 Скачать 156.24 Kb. Скачать 156.24 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение Высшего профессионального образования Рязанский Государственный Радиотехнический Университет Кафедра АИТУ Контрольная работа по дисциплине: «Теория автоматического управления» Задание № 1, вариант № 1 Выполнил: студент группы 3030 Головастов Е. Проверил: Уваев А.И. Рязань 2017 г. Содержание Краткие теоретические сведения 3 Передаточные функции САУ 3 Определение установившихся ошибок отработки типовых задающих воздействий 4 Понятие устойчивости 7 Критерий устойчивости Гурвица 8 Расчетная часть 10 Задание на контрольную работу 10 Определение передаточных функций системы и составление дифференциального уравнения, связывающего выходной сигнал системы с внешними воздействиями 11 Определение желаемого коэффициента усиления системы и коэффициента усиления усилителя исходя из заданной точности 13 Определим по критерию Гурвица устойчивость замкнутой системы при значении коэффициента усиления, полученного в п.2 13 Построение ЛАЧХ разомкнутой системы 14 Список используемых источников 17 1 Краткие теоретические сведения 1.1 Передаточные функции САУ Правила преобразования схем Последовательное соединение — это соединение, при котором выходная величина каждого предыдущего звена является входом последующего.  Рисунок 1 – последовательное соединение звеньев
Соединение звеньев с обратной связью:  Рисунок 2 – соединение звеньев с обратной связью
Передаточные функции замкнутых одноконтурных САУ Рассмотрим наиболее общую структуру линейных систем управления с одним входом и одним выходом (SISO-систем). Вначале рассмотрим так называемый номинальный контур, включающий регулятор, взаимодействующий с номинальной моделью в контуре обратной связи.  Рисунок 3 – структура линейных систем управления с одним входом и одним выходом Передаточная функция разомкнутой системы:
Передаточная функция замкнутой системы:
Передаточная функция по выходному возмущению:
Передаточная функция по ошибке:
1.2 Определение установившихся ошибок отработки типовых задающих воздействий К типовым задающим воздействиям относятся воздействия, представленные степенными функциями времени:
и гармонической функцией:
Величину установившейся ошибки воспроизведения для степенных воздействий целесообразно вычислять по формуле:
При выводе последней формулы использована известная в операционном исчислении теорема о конечном значении оригинала:
Изображение рассматриваемой степенной функции имеет вид:
В результате имеем:
Представляя передаточную функцию разомкнутой системы в стандартной форме:
где 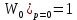 — нормирования ПФ, ν — порядок астатизма, k — коэффициент усиления, получаем ПФ по ошибке в следующем виде: — нормирования ПФ, ν — порядок астатизма, k — коэффициент усиления, получаем ПФ по ошибке в следующем виде:
Тогда
Анализируя последнюю формулу при разных значениях порядка астатизма и степени задающего воздействия, приходим к выводу, что если:
Случай ν = r = 0 соответствует ступенчатой функции 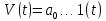 и нулевому порядку астатизма системы. Установившаяся ошибка в этом случае называется статической ошибкой и нулевому порядку астатизма системы. Установившаяся ошибка в этом случае называется статической ошибкой 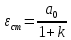 , соответственно система, имеющая в установившемся режиме при постоянном задающем воздействии ошибку, зависящую от величины , соответственно система, имеющая в установившемся режиме при постоянном задающем воздействии ошибку, зависящую от величины 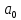 воздействия, называется статической. воздействия, называется статической.Система, порядок астатизма которой не равен нулю, т.е. ν = 1,2,... не имеет статической ошибки и называется астатической. Случай ν = r, r = 1,2,... определяет установившиеся ошибки, которые имеют названия, соответствующие физическому смыслу параметра 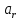 степенной функции. В частности, при степенной функции. В частности, при 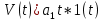 и ν = 1 и ν = 1установившаяся ошибка называется ошибкой по скорости, т.е. 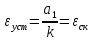 ; при ; при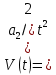 и ν = 2 установившаяся ошибка называется ошибкой по ускорению и ν = 2 установившаяся ошибка называется ошибкой по ускорению 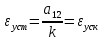 . .Случай ν = r + 1 соответствует тому, что степень множителя p в числителе ПФ по ошибке  равна степени знаменателя в изображении входного воздействия. равна степени знаменателя в изображении входного воздействия.Это приводит к нулевой установившейся ошибке. Следовательно, если порядок астатизма системы ν на единицу больше степени r входного степенного воздействия, то система является селективно инвариантной по отношению к этому воздействию. Определение. Селективная инвариантность — это равенство нулю установившейся ошибки от входного воздействия, изображение которого имеет полюсы, совпадающие с нулями ПФ ошибки. Для достижения селективной инвариантности ошибки от задающего воздействия астатизм системы обеспечивается наличием интегрирующих звеньев в прямом тракте системы, число которых должно быть не менее r + 1. 1.3 Понятие устойчивости Вопрос об устойчивости систем автоматического управления является основным в теории автоматического управления. С практической точки зрения неустойчивая система не имеет никакого смысла. Инженер-проектировщик в первую очередь должен обеспечить устойчивость системы управления, и только после этого позаботиться об удовлетворении других требований к динамике системы. Любая замкнутая система управления является либо устойчивой, либо неустойчивой. При таком подходе обычно речь идёт о так называемой абсолютной устойчивости. Систему, обладающую абсолютной устойчивостью, называют просто устойчивой, отбрасывая слово «абсолютная». Если же замкнутая система является устойчивой, то речь должна идти о степени этой устойчивости, и тогда пользуются понятием относительной устойчивости. Система автоматического управления состоит из объекта управления и управляющего устройства (регулятора). Задачей управляющего устройства является поддержание системы в состоянии равновесия (т.е. в таком состоянии, при котором регулируемая величина – угол поворота, скорость, температура, напряжение и т.д. – сохраняет постоянное значение). Если система отклонилась от состояния равновесия (рабочей точки), то управляющее устройство вновь должно привести ее к этому состоянию. Поэтому проектирование системы начинается с определения тех состояний равновесия, которые система должна поддерживать. Состояние равновесия нелинейной системы можно определить или аналитическим путем, решая нелинейное алгебраическое уравнение, соответствующее постоянству управляемой величины системы, или графоаналитическим путем, имея статические характеристики, связывающие выходные и входные величины всех элементов системы. Для суждения об устойчивости состояния равновесия необходимо вывести систему из этого состояния путем приложения внешнего возмущения и наблюдать характер свободного движения системы после прекращения действия этого возмущения. Состояние равновесия системы автоматического управления будет устойчивым, если после устранения возмущающего воздействия система с течением времени вновь возвращается к этому состоянию. Состояние равновесия системы является неустойчивым, если после устранения возмущающего воздействия система продолжает удаляться от состояния равновесия. Величина отклонения от состояния равновесия определяет «устойчивость в малом» или «устойчивость в большом». Если анализ устойчивости системы проводится при малых отклонениях от состояния равновесия, то говорят об «устойчивости в малом». Если же анализируется поведение системы при больших отклонениях от состояния равновесия, то говорят об «устойчивости в большом». 1.4 Критерий устойчивости Гурвица О наличии корней с положительной вещественной частью можно судить по коэффициентам характеристического уравнения. Правила, по которым можно определить, имеет ли система корни с положительной вещественной частью, были формулированы независимо друг от друга английским математиком Раусом и швейцарским математиком Гурвицем, и получили название критериев Рауса и Гурвица. Приведем без доказательства формулировку критерия Гурвица. Пусть дано характеристическое уравнение замкнутой системы
Прежде всего проверяется необходимое условие устойчивости — 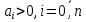 . Если оно не выполняется, то система не является асимптотически устойчивой. . Если оно не выполняется, то система не является асимптотически устойчивой.При выполнении данного условия составляется матрица Гурвица по следующему правилу. По главной диагонали последовательно выписывают коэффициенты 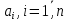 характеристического многочлена начиная с характеристического многочлена начиная с 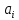 . Вниз от элементов главной диагонали столбцы заполняют коэффициентами . Вниз от элементов главной диагонали столбцы заполняют коэффициентами 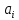 с последовательно убывающими с последовательно убывающимииндексами и нулями, когда индексы становятся отрицательными. Вверх от главной диагонали столбцы заполняются коэффициентами 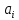 с возрастающими индексами с возрастающими индексамии нулями, когда индекс должен бы быть больше n. Строки матрицы состоят из коэффициентов 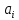 либо только с нечетными, либо только с четными индексами и либо только с нечетными, либо только с четными индексами инулями: 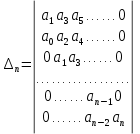 . .Критерий Гурвица гласит: система устойчива, если при 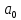 > 0 главный определитель Гурвица и все его диагональные миноры > 0 главный определитель Гурвица и все его диагональные миноры 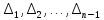 положительны, причем положительны, причем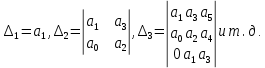 Если главный определитель 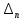 равен нулю, то система находится на границе равен нулю, то система находится на границеустойчивости. Так как 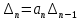 , то возможно два случая: , то возможно два случая: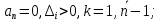 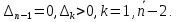 В первом случае говорят об апериодической границе устойчивости, во втором — о колебательной границе устойчивости. Расчетная часть 2.1 Задание на контрольную работу Определить передаточные функции системы и составить дифференциальное уравнение, связывающее выходной сигнал системы с внешними воздействиями. Исходя из заданной точности определить желаемый коэффициент усиления системы и коэффициент усиления усилителя. По критерию Гурвица определить устойчивость системы при значении коэффициента усиления системы, полученного в п.2. Построить ЛАЧХ неизменяемой части системы. Система автоматической установки масштабных коэффициентов в аналоговом вычислительном комплексе. При ручной установке масштабных коэффициентов неизбежны субъективные ошибки. Для уменьшения величины ошибок и увеличения скорости установки масштабных коэффициентов применяется автоматическая система, имеющая структурную схему, показанную на рисунке 4.  Рисунок 4 – Структурная схема системы Система работает следующим образом. С помощью клавишного устройства на вход следующей системы подается напряжение 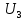 , пропорциональное требуемому углу , пропорциональное требуемому углу 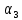 поворота настраиваемого потенциометра. Оно сравнивается напряжением поворота настраиваемого потенциометра. Оно сравнивается напряжением 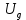 , пропорциональным действующему углу , пропорциональным действующему углу 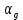 – поворота настраиваемого потенциометра. Напряжение – поворота настраиваемого потенциометра. Напряжение 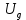 снимается с потенциометрического преобразователя снимается с потенциометрического преобразователя 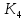 . .При отклонении угла 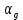 от угла от угла 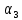 напряжение рассогласования напряжение рассогласования 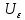 , проходя по прямой цепи управления, состоящей из модулятора , проходя по прямой цепи управления, состоящей из модулятора 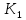 , усилителя переменного тока с передаточной функцией , усилителя переменного тока с передаточной функцией 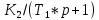 вызывает поворот вала настраиваемого потенциометра до полного устранения рассогласования. вызывает поворот вала настраиваемого потенциометра до полного устранения рассогласования.Исходные данные и требования к системе:
Определение передаточных функций системы и составление дифференциального уравнения, связывающего выходной сигнал системы с внешними воздействиями Передаточная функция разомкнутой системы определяется по формуле (1): 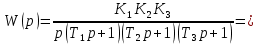 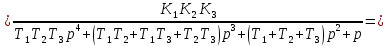 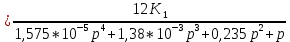 Передаточную функцию замкнутой системы находим по формуле (2): 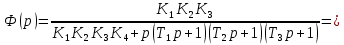 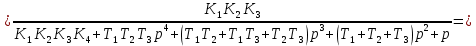 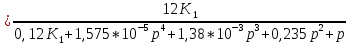 Передаточную функцию замкнутой системы по возмущению определим по формуле (3): 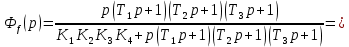 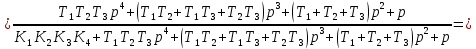 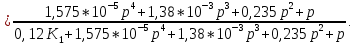 Передаточную функцию замкнутой системы по ошибке находим по формуле (4): 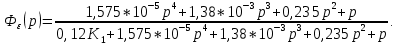 Составим дифференциальное уравнение замкнутой системы. Для этого сперва запишем уравнение замкнутой системы в изображениях: 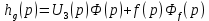 = =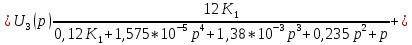 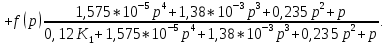 Перенесем знаменатель в левую часть: 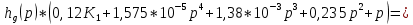 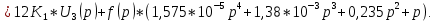 Теперь перейдём от изображений к оригиналам. Чтобы осуществить этот переход, у в левой части выражения произведём замену 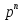 на на 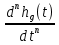 ,а в правой – на ,а в правой – на 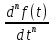 : :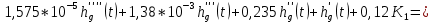 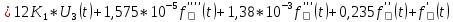 2.3 Определение желаемого коэффициента усиления системы и коэффициента усиления усилителя исходя из заданной точности Исследуемая система является системой первого порядка астатизма со входным сигналом вида: v(t) = 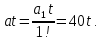 В данном случае установившаяся ошибка вычисляется по формуле (6). Из неё найдём желаемый коэффициент усиления всей системы: 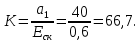  Теперь найдём коэффициент усиления усилителя 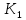 : :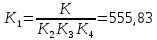 ПФ разомкнутой системы: 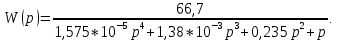 ПФ замкнутой системы: 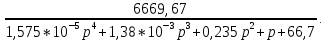 2.4 Определим по критерию Гурвица устойчивость замкнутой системы при значении коэффициента усиления, полученного в п.2 Характеристическое уравнение нашей системы имеет вид: А(p) = 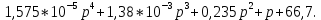 Прежде чем строить матрицу Гурвица, проверим необходимое условие устойчивости: все коэффициенты 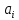 , i = 0,n характеристического уравнения должны быть больше нуля. Все коэффициенты , i = 0,n характеристического уравнения должны быть больше нуля. Все коэффициенты 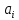 , больше нуля. , больше нуля.Составим матрицу Гурвица для уравнения: 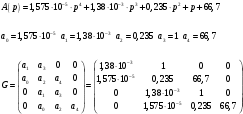 Найдем определители этой матрицы: 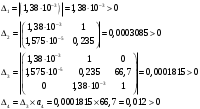 Определители всех 4 порядков положительные; замкнутая система устойчива. 2.5 Построение ЛАЧХ разомкнутой системы График частотных характеристик системы построим при помощи системы MATLAB: 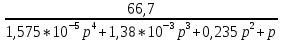  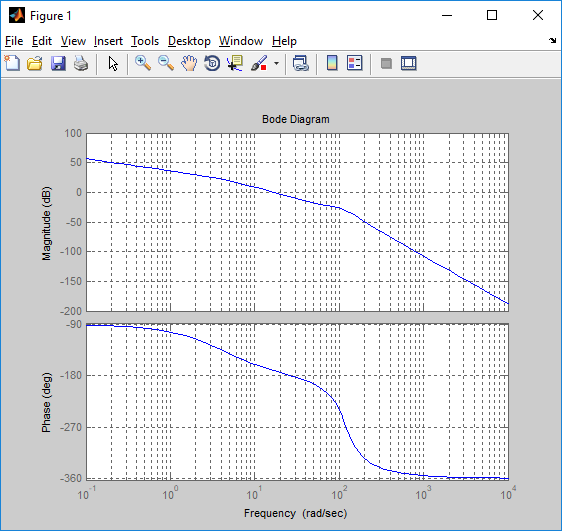 Рисунок 4 - ЛАЧХ разомкнутой системы По полученным частотным характеристикам видим, что система устойчива, т.к. на частоте среза ЛАЧХ значение ЛФЧХ составляет: φ(ω) > –180º. Построим годограф Найквиста разомкнутой системы: 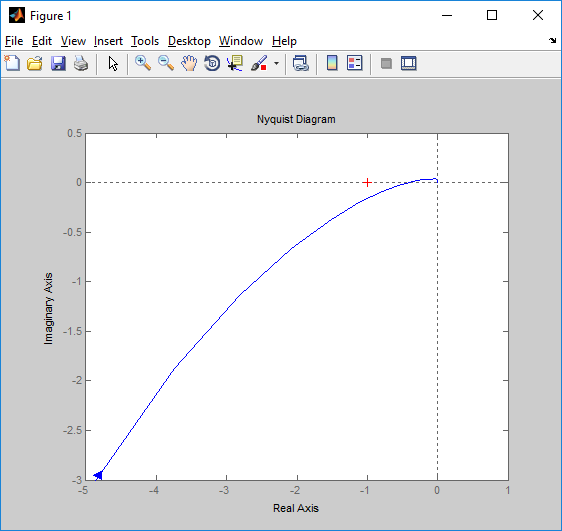 Рисунок 5 – Годограф Найквиста разомкнутой системы Из критерия Найквиста следует, что система устойчива, т.к. АФХ не охватывает критическую точку (-1, j0). Список используемых источников Воронов А.А.: Теория автоматического управления, Москва: издательство Высшая школа, 1986. — 367 с, ил. Афанасьев, Калмановский, Носов: Математическая теория конструирования систем управления, Москва: издательство Высшая школа, 2003. — 615 с. Певзнер Л.Д.: Теория систем управления, Москва: Издательство Московского государственного горного университета 2002. – 472 с. Шишмарев В.Ю.: Основы автоматического управления, Москва: издательство Академия, 2008. – 347 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||

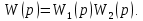
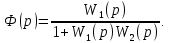
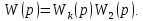
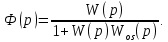
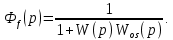
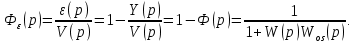
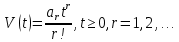
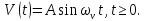
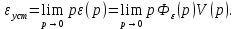
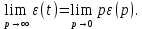
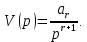
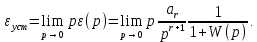
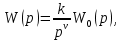
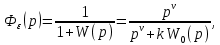
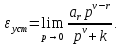
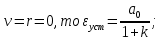
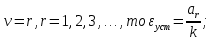
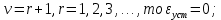
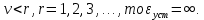
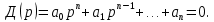
 = 3
= 3 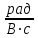
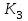 = 4
= 4 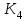 = 0,01
= 0,01 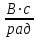
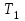 = 0,015 с
= 0,015 с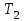 = 0,07 с
= 0,07 с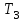 = 0,15 с
= 0,15 с