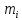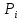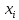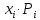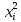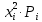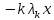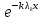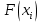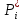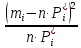Математическое моделирование систем и процессов ДВГУПС. Мат мод широков вар 1 зад 1. Контрольная работа Вариант 291 Задача 1 Математическая статистика и законы распределения
 Скачать 141.73 Kb. Скачать 141.73 Kb.
|
|
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМ И ПРОЦЕССОВ Контрольная работа Вариант 291 Задача 1Математическая статистика и законы распределения В результате обработки отчетных данных на станции установлены моменты фактического прибытия четных поездов на станцию, полученные в результате натурных наблюдений за двое суток (табл. 1). Таблица 1 Моменты фактического прибытия поездов на станцию
Необходимо установить какому теоретическому закону распределения подчиняется интервал прибытия поездов на станцию. Для этого требуется следующее. Составить статистический ряд интервалов прибытия четных грузовых поездов на сортировочную станцию. Установить основные временные параметры входящего на станцию поездопотока (среднее значение, дисперсию, среднее квадратическое отклонение и коэффициент вариации). Построить гистограмму распределения вероятностей появления интервалов между поездами. Решение. Процедура вычисления основных характеристик статистического распределения следующая. Так как в исходных данных приведены моменты прибытия поездов, а требуется исследовать интервалы прибытия, то необходимо обработать исходные данные (определить сами интервалы прибытия). Интервалы определяются как разность между временем прибытия последующего поезда и временем прибытия предыдущего поезда. 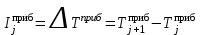 , (27) , (27)где 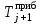 – время прибытия последующего поезда, ч, мин; – время прибытия последующего поезда, ч, мин; 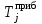 – время прибытия предыдущего поезда, ч, мин. – время прибытия предыдущего поезда, ч, мин.Тогда первый и второй интервалы прибытия будут равны: 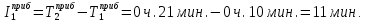 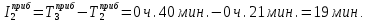 Результаты расчетов всех интервалов прибытия представляются в табл. 2. Таблица 2 Интервалы прибытия поездов
Далее производится группирование интервалов по разрядам. Количество разрядов определяется по формуле (1): 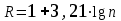 , (1) , (1)где 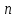 – общее число наблюдений; – общее число наблюдений;Шаг разряда – величину интервала группирования – можно определить по формуле 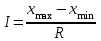 , (2) , (2)где 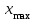 , , 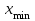 – наибольшее и наименьшее значения случайной величины из всей совокупности исходных данных; – наибольшее и наименьшее значения случайной величины из всей совокупности исходных данных; 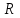 – количество разрядов (классов). – количество разрядов (классов).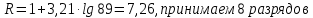 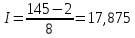 Определяются значения интервалов прибытия на границах разрядов (табл. 3). Таблица 3 Значения интервалов прибытия на границах разрядов
Установив шаг разряда и, рассчитав значения границ разряда, приступают к группированию исходных данных (интервалов прибытия) по разрядам. В процессе группирования устанавливается, сколько интервалов 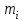 попало в разряд попало в разряд 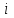 (значения от (значения от 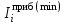 до до 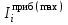 ). Для удобства применения формул обозначим исследуемую величину интервала прибытия поездов через ). Для удобства применения формул обозначим исследуемую величину интервала прибытия поездов через 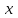 . Последующие расчеты основных параметров статистического рада целесообразно проводить в форме таблицы путем заполнения отдельных колонок, в которые сводятся все промежуточные результаты вычислений (табл. 4). . Последующие расчеты основных параметров статистического рада целесообразно проводить в форме таблицы путем заполнения отдельных колонок, в которые сводятся все промежуточные результаты вычислений (табл. 4).Таблица 4 Обработка статистического ряда интервалов между моментами прибытия поездов на станцию
Математическое ожидание определяется суммированием произведений среднего (срединного) значения разрядов статистического ряда на соответствующие частости наблюдаемых величин 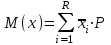 , (3) , (3)где 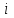 – обозначение разряда; – обозначение разряда; 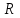 – число разрядов; – число разрядов; 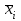 – среднее значение случайной величины в разряде – среднее значение случайной величины в разряде 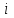 ; ; 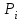 – частость разряда, – частость разряда,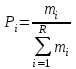 ; (4) ; (4)где 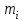 – количество значений случайной величины в разряде – количество значений случайной величины в разряде 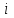 ; ; 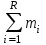 – суммарное количество наблюдений, – суммарное количество наблюдений, 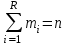 . .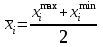 , (5) , (5)где 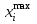 , , 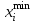 – наибольшее и наименьшее значения случайной величины в – наибольшее и наименьшее значения случайной величины в 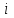 -м разряде. -м разряде.В некоторых случаях определяется величина, обратная математическому ожиданию и называемая интенсивностью появления случайной величины в единицу времени 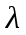 . .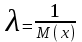 . (6) . (6)Индивидуальные значения величин отличаются друг от друга, отклоняясь от средней величины в ту или другую сторону. Величина этого отклонения показывает, в какой мере значения отличаются и друг от друга, т. е. размер вариации признака. Показателями размера вариации служат дисперсия, среднее квадратическое отклонение и коэффициент вариации. Дисперсия, представляет собой математическое ожидание квадратов отклонений случайной величины от ее математического ожидания. 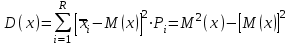 , (7) , (7)где 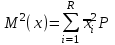 – второй начальный момент случайной величины. – второй начальный момент случайной величины.Квадратный корень из дисперсии носит название среднего квадратического отклонения 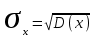 . (8) . (8)Коэффициент вариации – относительная мера рассеивания случайной величины от среднего значения – определяется как отношение среднего квадратического отклонения к математическому ожиданию 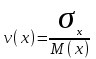 . (9) . (9)В зависимости от целей исследования могут определяться следующие дополнительные характеристики случайной величины: коэффициент асимметрии, коэффициент эксцесса, мода случайной величины, медиана случайной величины. Для каждого разряда наблюдаемых величин подсчитывают их количество и определяют частость по формуле (4). Далее по формулам (3) и (7) находят математическое ожидание и дисперсию. И, наконец, по формулам (8) и (9) рассчитывают соответственно среднее квадратическое отклонение и коэффициент вариации. Из табл. 4 получаем значение математического ожидания, мин, 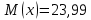 – дисперсия интервала прибытия поездов: 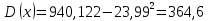 – среднее квадратическое отклонение, мин: 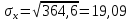 – коэффициент вариации: 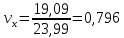 Интенсивность поступления поездов на станцию , поезда/мин, рассчитывается по формуле (6) 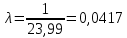 На основании расчетных характеристик (табл. 4) строится гистограмма распределения интервалов прибытия поездов (рис. 5). На горизонтальной оси гистограммы откладываются разряды и на каждом их них, как на основании, строят прямоугольник, площадь которого равна частости разряда. Ордината гистограммы определяется по формуле 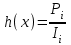 , (28) , (28)где 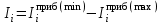 – шаг конкретного – шаг конкретного 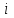 -го разряда. -го разряда.Если шаг всех разрядов одинаков, то принимается значение 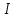 . .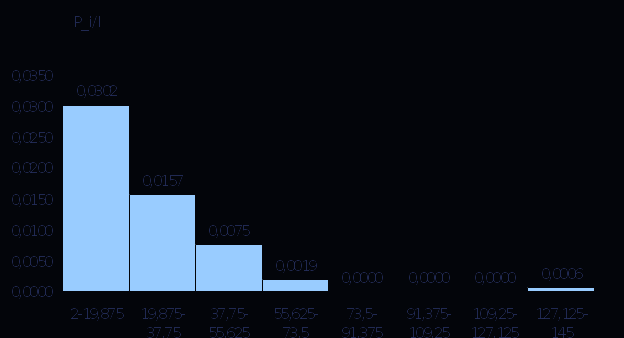 Рис. 5. Гистограмма распределения интервалов прибытия поездов Исходя из внешнего вида гистограммы и представляя себе графики теоретических законов распределения случайных величин, подбирается визуально наиболее близкий теоретический закон распределения и проверяется гипотеза о согласовании выбранного закона со статистическими данными. Кроме того, при выдвижении гипотезы о том или ином законе распределения можно рассчитать параметр Эрланга 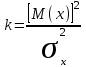 . (18) . (18)Рассчитаем: 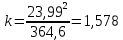 откуда следует, что необходимо рассмотреть закон распределения Эрланга с параметром равным 1 или 2. При k=1 функция распределения Эрланга выглядит следующим образом: 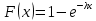 Проверка осуществляется по критерию согласия Пирсона по формуле (23) и правилу Романовского по формуле (26). Расчет критерия согласия Пирсона удобнее всего вести в таблице (табл. 5). 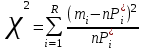 , (23) , (23)где 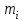 – число значений случайной величины в – число значений случайной величины в 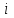 -м разряде; -м разряде; 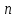 – количество наблюдений; – количество наблюдений; 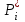 – теоретическая вероятность, принимается в зависимости от выбранного закона распределения случайной величины по расчетным формулам или специальным таблицам [5, прил. 1–4, 6–9]. – теоретическая вероятность, принимается в зависимости от выбранного закона распределения случайной величины по расчетным формулам или специальным таблицам [5, прил. 1–4, 6–9].Теоретическая вероятность 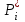 интервалов определенной величины в разряде интервалов определенной величины в разряде 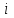 в их общей совокупности равна в их общей совокупности равна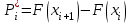 , (24) , (24)где 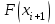 и и 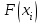 – функция закона распределения соответственно на верхней и нижней границах – функция закона распределения соответственно на верхней и нижней границах 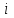 -го разряда. -го разряда.Распределение 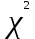 зависит от параметра зависит от параметра 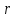 , называемого числом степеней свободы (количество независимых параметров случайной величины) распределения и равного разности между числом разрядов и числом независимых условий (связей), наложенных на частоты , называемого числом степеней свободы (количество независимых параметров случайной величины) распределения и равного разности между числом разрядов и числом независимых условий (связей), наложенных на частоты 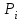 . . 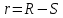 , (25) , (25)где 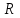 – число разрядов, на которое разбивается общее число наблюдений; – число разрядов, на которое разбивается общее число наблюдений; 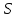 – число наложенных связей. – число наложенных связей.Количество наложенных связей 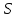 определяется числом параметров (числовых характеристик) принятого закона распределения плюс 1 и зависит только от принятого закона распределения случайной величины. Так, для показательного распределения количество параметров равно одному – определяется числом параметров (числовых характеристик) принятого закона распределения плюс 1 и зависит только от принятого закона распределения случайной величины. Так, для показательного распределения количество параметров равно одному – 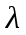 , зависящему от , зависящему от 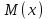 , следовательно, число наложенных связей , следовательно, число наложенных связей 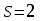 . .Для нормального распределения количество параметров равно двум – 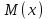 и и 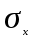 , следовательно, число наложенных связей , следовательно, число наложенных связей 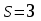 . .Для распределения Эрланга количество параметров равно двум – 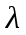 и и 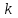 , которые, в свою очередь, являются производными от , которые, в свою очередь, являются производными от 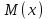 и и 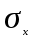 , следовательно, число наложенных связей , следовательно, число наложенных связей 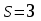 . .По специальным таблицам [4, прил. 5] можно для каждого значения 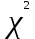 и числа степеней свободы и числа степеней свободы 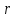 найти найти 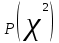 – вероятность того, что величина, распределенная по закону – вероятность того, что величина, распределенная по закону 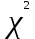 , превзойдет это значение. , превзойдет это значение. Последовательность применения критерия 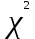 к оценке согласованности теоретического и статистического распределений следующая: к оценке согласованности теоретического и статистического распределений следующая:определяют числовые характеристики эмпирического распределения; по их значениям и внешнему виду гистограммы распределения выдвигают гипотезу о возможности замены статистического распределения теоретическим 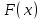 ; ;по формуле (24) находят меру расхождения 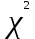 ; ;по формуле (25) определяют число степеней свободы 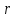 ; ;по 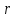 и и 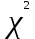 находят вероятность согласованности эмпирического распределения принятому теоретическому. находят вероятность согласованности эмпирического распределения принятому теоретическому.Кроме критерия согласия Пирсона, для оценки степени согласованности статистического и теоретического распределений применяют и другие критерии, например правило Романовского. По Романовскому, гипотеза о принятом теоретическом законе распределения считается правдоподобной, если соблюдается следующее неравенство 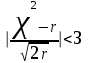 , (26) , (26)где 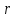 – число степеней свободы. – число степеней свободы. Если его значение меньше 3, то расхождение между теоретическим и эмпирическим распределениями несущественно; если больше 3 – существенно. Это правило менее строго, чем критерий Пирсона, и применяется в расчетах, когда нет необходимости исследовать степень близости статистического и теоретического распределений. Таблица 5 Характеристики распределения интервалов между поступающими в переработку поездами
Как видно из последней колонки табл. 5, критерий согласия Пирсона 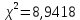 Так как разрядов – 8, а наложенных связей для Эрланговского закона распределения – 1, то число степеней свободы определится: 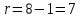 Пользуясь приложением 5 [4], находится, что вероятность 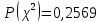 Значит, гипотеза о Эрланговском распределении интервалов поступления поездов на станцию с параметром k=1 требует дополнительной проверки. Проверку данной гипотезы производим по правилу Романовского: 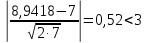 Следовательно, расхождение между теоретическим и эмпирическим распределениями не столь существенно и гипотеза об Эрланговском законе распределения интервала прибытия поездов на станцию с параметром k=1 правдоподобна. Число бригад ПТО в парке приема рассчитывается, исходя из одного из условий бесперебойной работы станции 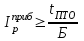 , (29) , (29) где 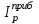 – расчетный интервал прибытия поездов; – расчетный интервал прибытия поездов; 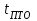 – время на техническое обслуживание поезда одной бригадой; – время на техническое обслуживание поезда одной бригадой; 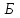 – число бригад. – число бригад.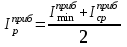 , (30) , (30)где 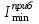 – минимальный интервал между поездами, прибывающими на станцию, мин,; – минимальный интервал между поездами, прибывающими на станцию, мин,; 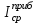 – средний интервал прибытия поездов, мин, – средний интервал прибытия поездов, мин, 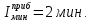 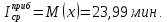 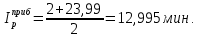 Время на техническое обслуживание 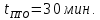 Число бригад из формулы (29) рассчитывается 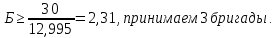 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||