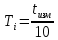|
механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
Лабораторная работа №13
ФИЗИЧЕСКИЙ МАЯТНИК
Цель работы: Изучить гармонические колебания на примере движения физического маятника. Определить момент инерции физического маятника методом колебаний.
Требуемое оборудование: Модульный учебный комплекс МУК-М1: рабочий узел «маятник», стержень, грузы, электронный секундомер ЭС1.
Краткое теоретическое введение
Физический маятник представляет собой твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси О, не проходящей через его центр масс С (рис.1).
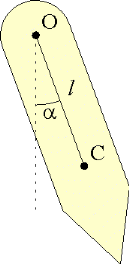
рис. 1
Дифференциальное уравнение, описывающее колебания физического маятника:
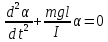 (1) (1)
где m – масса маятника; l – расстояние от оси вращения (точка О) до центра масс (точка С); I – момент инерции физического маятника относительно оси вращения.
Обозначив 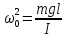 получим: получим:
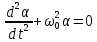 (2) (2)
Решением данного дифференциального уравнения является функция (убедиться в справедливости решения (6) можно путем непосредственной подстановки его в уравнение (5)):
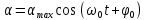 , (3) , (3)
где 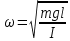 – собственная циклическая частота колебаний физического маятника; – собственная циклическая частота колебаний физического маятника; 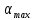 – максимальное значение α; φ0 – начальная фаза. – максимальное значение α; φ0 – начальная фаза.
Учитывая связь между собственной циклической частотой физического маятника и периодом колебаний, получим выражение для периода:
 (4) (4)
Методика эксперимента
Рассмотрим физический маятник, конструкция которого представлена на рис.2а. Он состоит из барабана массой m1, стержня массой m2 и двух грузов с одинаковыми массами m3, которые могут перемещаться вдоль стержня. Вращение маятника происходит относительно оси, проходящей через точку О.
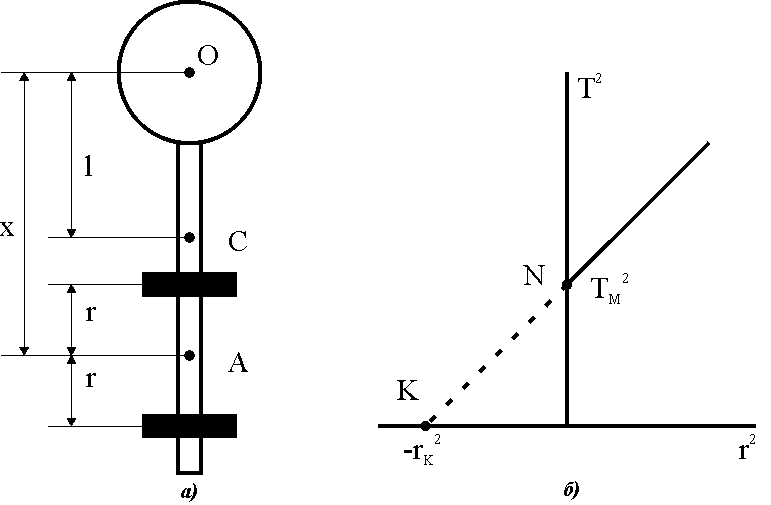
рис. 2
Если грузы смещать относительно произвольно выбранной точки А на одинаковые расстояния r, то положение центра масс l (точка С) относительно точки О остается неизменным. При этом момент инерции Iтакого маятника будет меняться по закону:
 , (5) , (5)
где 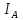 – момент инерции маятника, при положении грузов m3 в точке А. – момент инерции маятника, при положении грузов m3 в точке А.
Подставим выражение (8) в (7), и возведем в квадрат
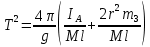 (6) (6)
где 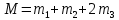 – масса маятника. – масса маятника.
Из этого выражения видно, что график функции 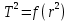 представляет собой функцию типа представляет собой функцию типа 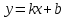 (рис.2б). (рис.2б).
Для нахождения момента инерции 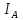 необходимо полученный график экстраполировать до пересечения с осью r2 и по точке пересечения К найти значение необходимо полученный график экстраполировать до пересечения с осью r2 и по точке пересечения К найти значение 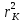 . В этом случае . В этом случае 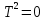 , а следовательно выражение можно представить в виде , а следовательно выражение можно представить в виде
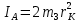 (7) (7)
Для нахождения расстояния от оси вращения до центра масс l необходимо найти значение 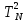 , соответствующее на графике точке N: , соответствующее на графике точке N:
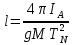 (8) (8)
Пользуясь выражением (7) можно экспериментально найти значения момента инерции рассмотренного физического маятника
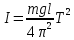 (9) (9)
Переведите секундомер в режим №4. Выведете маятник из положения равновесия на небольшой угол 5 - 10°. Отпустите груз и нажмите кнопку «Пуск» секундомера. Отсчитайте время tизм равное 10 колебаниям и нажмите кнопку «Стоп/Сброс» секундомера. Период колебаний можно рассчитать по формуле 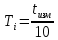
Порядок выполнения работы
Установите симметрично грузы относительно точки А (рекомендуемое значение расстояния от оси вращения указано в таблице с исходными данными) на минимальное расстояние r.
Измерьте время 10 колебаний и вычислите период колебаний T.
Увеличивая расстояние r, измерьте соответствующие периоды колебаний. Проведите 5 измерений. Данные занесите в таблицу.
Таблица
№
|
|
Ti
|
|
ri
|
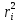
|
I (теор.)
|
I (эксп.)
|
1
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
Постройте график зависимости 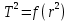 . Убедитесь, что полученный график представляет собой линейную функцию. . Убедитесь, что полученный график представляет собой линейную функцию.
Экстраполируйте полученный график до пересечения с осью r2. По графику найдите точки пересечения с осями 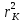 и и 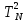 . .
С помощью выражений (7) и (8) найдите значения 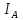 и l. Сравните полученное значение l с указанным в паспорте прибора расстоянием от оси вращения до центра тяжести маятника. и l. Сравните полученное значение l с указанным в паспорте прибора расстоянием от оси вращения до центра тяжести маятника.
Используя формулу (5), постройте теоретическую зависимость 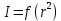 . .
В тех же осях, используя формулу (9), постройте практическую зависимость 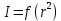 . Сравните полученные результаты. . Сравните полученные результаты.
Сделайте выводы.
Контрольные вопросы
Что такое физический маятник?
Чему равен период колебаний физического маятника?
Выведите уравнение колебаний физического маятника. Получите его решение.
Как определяется момент инерции физического маятника в работе?
Выведите формулу (9).
Используя теорему Штейнера выведите формулу для момента инерции физического маятника использовавшегося в работе.
Совпадают ли теоретически и практически полученные графики?
*Предложите методику эксперимента, в котором бы учитывалось затухание колебаний, и имелась возможность расчета декремента затуханий колебаний.
|
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.
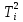
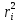
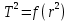 . Убедитесь, что полученный график представляет собой линейную функцию.
. Убедитесь, что полученный график представляет собой линейную функцию.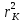 и
и 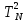 .
. 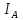 и l. Сравните полученное значение l с указанным в паспорте прибора расстоянием от оси вращения до центра тяжести маятника.
и l. Сравните полученное значение l с указанным в паспорте прибора расстоянием от оси вращения до центра тяжести маятника.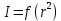 .
. 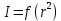 . Сравните полученные результаты.
. Сравните полученные результаты.

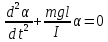 (1)
(1)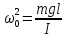 получим:
получим: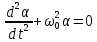 (2)
(2)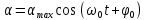 , (3)
, (3)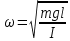 – собственная циклическая частота колебаний физического маятника;
– собственная циклическая частота колебаний физического маятника;  – максимальное значение α; φ0 – начальная фаза.
– максимальное значение α; φ0 – начальная фаза. (4)
(4)
 , (5)
, (5)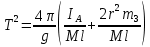 (6)
(6)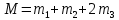 – масса маятника.
– масса маятника.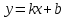 (рис.2б).
(рис.2б).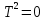 , а следовательно выражение можно представить в виде
, а следовательно выражение можно представить в виде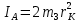 (7)
(7)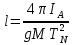 (8)
(8)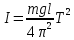 (9)
(9)