механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
 Скачать 0.7 Mb. Скачать 0.7 Mb.
|
ЧАСТЬ I. ЛАБОРАТОРНЫЕ РАБОТЫ |
| y (мм) | 1 | 1 | 1 | 0.5 |
| m | 10 | 20 | 50 | 25 |
| ∆x (мм) | 0.1 | 0.05 | 0.02 | 0.02 |
Методика эксперимента
Штангенциркуль

рис. 3
Линейные нониусы применяются в конструкциях штангенциркуля. Штангенциркуль (рис.3) состоит из миллиметрового масштаба (шкалы прибора - а), жестко связанного с щекой с. Вдоль масштаба может перемещаться нониус – b. Подвижная часть штангенциркуля снабжена зажимным винтом. Когда между щеками отсутствует зазор, нулевые метки нониуса и шкалы совпадают.
При измерении наружных размеров детали нониус отодвигают и помещают деталь (g) между щеками c, которые затем сдвигают до соприкосновения с предметом и, закрепив подвижную щеку зажимом, производят отсчет. Число целых делений масштаба отсчитывается непосредственно по основной шкале прибора до нулевой метки нониуса, число долей деления – по нониусу.
При внутренних промерах, например, при измерении внутренних диаметров трубок (d), пользуются щеками, которые вводят внутрь трубки и разводят настолько, чтобы они плотно прилегли к внутренним стенкам, после чего производят отсчет по масштабу и нониусу.
Для измерения глубины используется рейка e.
Штангенциркуль служит для измерений, не требующих высокой точности.
Микрометр

рис. 4
Для более точных измерений применяют микрометрические инструменты. Они бывают нескольких типов: микрометр для наружных измерений (рис.4) состоит из массивной металлической скобы 7 и втулки 3, неподвижный упор 1 и микрометрический винт 2, жестко связанный с барабаном 5. Барабан 5, обычно делится на 100 или 50 делений. Поступательное перемещение винта измеряется по смещению среза барабана винта, вдоль шкалы 3. Шаг винта обычно равен 1 мм или 0.5 мм.
При измерении предмет помещают между упором 1 и микрометрическим винтом 2, вращая последний до тех пор, пока он не соприкоснётся с измеряемым предметом (до первого щелчка). Отсчет производится по горизонтальной шкале 3 и по шкале барабана 4. Цена деления шкалы 4 барабана может быть установлена следующим образом: если число деления круговой шкалы барабана m=50, а шаг микровинта h=0.5 мм, то одному полному обороту микровинта (и барабана) соответствует линейное перемещение края барабана по горизонтальной шкале на 0.5 мм. Следовательно, цена деления круговой шкалы барабана (линейное перемещение его при обороте на одно деление) будет равна
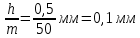
Эта величина является точностью микрометра.
Таким образом, при измерении по горизонтальной шкале отсчитывается размер измеряемого предмета с точностью до 0.5 мм. Сотые доли миллиметра отсчитываются по круглой шкале барабана и складываются с результатами отсчета по горизонтальной шкале. Число сотых долей соответствует делению шкалы барабана расположенному против продольной черты горизонтальной шкалы. Для равномерности нажима микрометрического винта на поверхность измеряемых тел микрометр снабжен фрикционной головкой 6 (трещоткой), вращение которой вызывает перемещение винта только до упора его в поверхность измеряемого тела с определенным нажимом, после чего фрикционная головка свободно прокручивается, издавая треск.
Различные микрометры могут иметь разные пределы измерения: 0 – 25, 50, 75 мм и т.д. до 1600 мм.
Порядок выполнения работы
Измерение диаметров проволок с помощью микрометра.
Изучить конструкцию микрометра. Проверить исправность прибора (нулевые отметки на горизонтальной шкале 3 и шкале барабана 4 должны совпадать).
Определить технические параметры микрометра: пределы измерения, шаг винта, точность микрометра.
Измерить диаметр пяти различных проволок (по 5 раз каждую на разных участках длины) и найти для каждой проволоки среднее значение диаметра.
Результаты измерений занести в таблицу 1.
Таблица 1
| № | d1 | 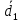 | d2 |  | d3 | 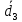 | d4 | 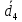 | d5 | 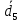 |
| мм | мм | мм | мм | мм | мм | мм | мм | мм | мм | |
| 1 | | | | | | | | | | |
| 2 | | | | | | | ||||
| 3 | | | | | | | ||||
| 4 | | | | | | | ||||
| 5 | | | | | | |
Измерение линейных размеров тела с помощью штангенциркуля. Вычисление плотности тела.
Изучить конструкцию и принцип действия штангенциркуля. Проверить исправность прибора (нулевые отметки масштаба и нониуса должны совпадать).
Измерить высоту трубки (h) по трем направлениям. Найти среднее значение высоты.
Измерить внешний (a) и внутренний (b) диаметры трубки по трем направлениям. Найти их средние значения.
Найти объем трубки по формуле
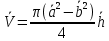 .
.Определить массу трубки, взвесив её на весах.
Найти плотность вещества трубки
 . Сравнить с табличным значением.
. Сравнить с табличным значением.Результаты измерений и вычислений занести в таблицу 2.
Вычислить абсолютную и относительную погрешности измерений (см. п. III.).
Сделать выводы.
Таблица 2
| № | h | 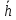 | a | 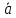 | b | 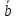 | m | 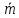 | 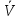 м3 | 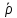 кг/м3 |
| м | м | м | м | м | м | кг | кг | |||
| 1 | | | | | | | | | | |
| 2 | | | | | ||||||
| 3 | | | | |
Подсчет погрешностей измерений объема трубки и ее плотности.
Ознакомиться с теорией подсчета погрешностей ЧАСТЬ II данного пособия.
Произвести подсчет погрешностей величины внешнего диаметра
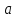 :
:Найти среднеквадратичную ошибку среднего арифметического значения величины
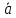 по формуле
по формуле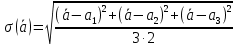
Задать коэффициент Стьюдента для доверительной вероятности α=0,95 и количестве измерений n=3,
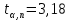 (см. приложение).
(см. приложение).Найти границы доверительного интервала для многократных измерений (случайная погрешность серии измерений)
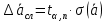
Оценить доверительный интервал (погрешность) однократного измерения a:
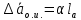 ,
, 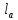 – параметр равномерного распределения для штангенциркуля равен точности нониуса, для аналитических весов цене деления.
– параметр равномерного распределения для штангенциркуля равен точности нониуса, для аналитических весов цене деления.Найти общую ошибку величины a:
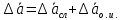
Аналогично по пп. 3 - 7 найти ошибки измерения внутреннего диаметра b; высоты h; массы m.
Найти абсолютную и относительную погрешности косвенного измерения объема цилиндрической трубки.
Абсолютная погрешность косвенного измерения находится по формуле
 . (*)
. (*)Возьмем частные производные от функции объема по соответствующим переменным. Частные производные берутся, как и обычные, но при условии, что все аргументы функции, кроме тех по которым вычисляется производная, считаются константами. Для простоты вывода опустим знак среднего.

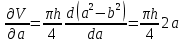

Подставим выражения для частных производных в (*)
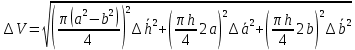
Помножим и поделим слагаемые под корнем на необходимые множители, что бы иметь возможность общий множитель вынести из под знака корня
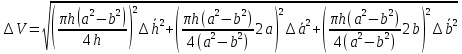
Вынесем из под корня
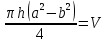 .
.Окончательная формула для подсчета абсолютной погрешности косвенного измерения объема примет вид
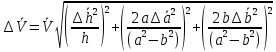
Относительная погрешность косвенного измерения величины
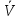 равна
равна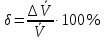
Округлить
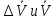 до первой значащей цифры после запятой. Ответ записать в виде
до первой значащей цифры после запятой. Ответ записать в виде 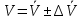 .
.Найти абсолютную и относительную погрешности измерения плотности по формулам:
 (**)
(**)
Округлить
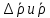 до первой значащей цифры после запятой. Ответ записать в виде
до первой значащей цифры после запятой. Ответ записать в виде 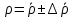 .
.Контрольные вопросы
Что такое нониус? Какие нониусы бывают и зачем они нужны?
Как выражается длина предмета, измеряемого масштабной линейкой с нониусом?
Чему равна цена деления и точность нониуса штангенциркуля?
Чему равна цена деления и точность нониуса микрометра?
Какие виды измерений существуют?
Какие виды погрешностей существуют и как они учитываются?
Какие методы определения погрешностей Вы знаете?
Какие погрешности Вами были учтены при выполнении лабораторной работы, а какие не учтены? Почему?
Как правильно записать результат измерений с учетом погрешности измерения?
Выведите формулу для подсчета абсолютной погрешности измерения плотности (**).

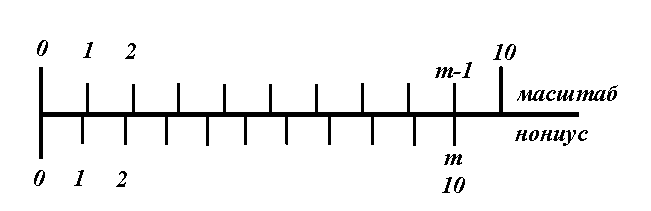
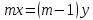 (1)
(1)
 (2)
(2)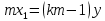

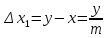

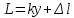 ,
, 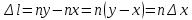

 , (3)
, (3) . Таким образом, погрешность нониуса равна половине его точности. В таблице приведены характеристики часто встречающихся линейных нониусов.
. Таким образом, погрешность нониуса равна половине его точности. В таблице приведены характеристики часто встречающихся линейных нониусов.