|
|
механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
Лабораторная работа №7
УПРУГОЕ СОУДАРЕНИЕ ШАРОВ
Цель работы: Изучить законы сохранения на примере центрального упругого удара шаров.
Приборы и принадлежности: Модульный учебный комплекс МУК-М1: рабочий узел «удар шаров», два шара разной массы.
Краткое теоретическое введение
Под процессом соударения физических тел понимают кратковременное взаимодействие тел на малых расстояниях или при контакте, которое приводит к резкому изменению величины и направления скоростей тел, а также к изменению их внутреннего состояния. Процессы соударения могут происходить как с макроскопическими телами, так и с микрочастицами (т.е. с атомами, молекулами и т.д.).
Проще всего рассматривать такие процессы в изолированных системах, состоящих из двух или нескольких тел. В такой системе всегда выполняется закон сохранения импульса. Вектор импульса всей системы тел остается неизменным по величине и направлению при любых процессах, происходящих в этой системе: при распаде тел на составные части, при слипании тел, при химических реакциях и т.д.
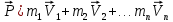
Сохраняется импульс и при соударениях.
Однако механическая энергия замкнутых систем физических тел, состоящая из кинетической энергии движения тел и потенциальной энергии их взаимодействия, может и не сохраняться: она может как увеличиваться так и уменьшаться. Так, если одно из тел системы разлетается на осколки под действием внутренних сил (например, при взрыве внутри тела), то при этом механическая энергия системы увеличивается за счет уменьшения внутренней энергии этого тела. Наоборот, если два каких-то тела из состава изолированной системы при столкновении соединяются в одно тело, то механическая энергия системы уменьшится, но увеличится внутренняя энергия этих тел. Подобные процессы могут происходить не только с макроскопическими телами, но и с микрочастицами. Например, если два атома при столкновении соединяются, при этом образуя молекулу, то механическая энергия образовавшейся молекулы меньше суммарной механической энергии столкнувшихся атомов, а излишек энергии переходит во "внутреннюю" энергию этой молекулы. Конечно, во всех случаях сохраняется полная энергия изолированной системы, состоящая из механической и внутренней энергии всех тел.
В принципе, можно представить себе процессы в замкнутой системе физических тел, которые происходят с сохранением механической энергии. Такие процессы принято называть упругими процессами. При этих процессах, не изменяется также внутренняя энергия всех тел, входящих в систему, т.е. не изменяется внутреннее состояние физических тел. Если таким процессом является соударение, то оно называется – абсолютно упругим соударением. Для макроскопических тел понятие абсолютно упругого соударения является идеализацией, так как хотя бы малая часть первоначальной механической энергии тел после удара переходит во внутреннюю энергию.
Для микрочастиц могут существовать и строго упругие соударения. Это связано с квантовым характером движения составных частей микрочастицы друг относительно друга. Например, пусть молекулы движутся с небольшими скоростями и имеют малые механические энергии. Колебания атомов в молекуле друг относительно друга квантуются, т.е. чтобы заставить атомы колебаться, необходимо сообщить молекуле энергию, не меньшую некоторой определенной порции. Если же сталкиваются две молекулы с малыми кинетическими энергиями, недостаточными для возбуждения колебаний, то при столкновении внутреннее состояние молекул не может измениться, и удар будет абсолютно упругим. Если же сталкивающиеся молекулы движутся с большими скоростями и имеют большие энергии, то при ударе возбуждаются колебания атомов в одной или обеих молекулах, часть энергии перейдет в энергию колебаний, и удар будет неупругим.
В данной работе рассматривается простейший случай соударения: центральный удар шаров.
Пусть два шара с массами m1 и m2 движутся со скоростями 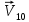 и и 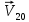 , а затем сталкиваются. После соударения изменится направление их движения и величина их скорости. , а затем сталкиваются. После соударения изменится направление их движения и величина их скорости.
Рассмотрим самый простой вид соударения - так называемый центральный удар. При этом векторы скоростей обоих шаров до удара лежат на линии, соединяющей центры шаров, причем векторы 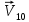 и и 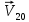 , могут быть направлены как навстречу друг другу, так и в одну сторону. Полный импульс этой системы, состоящей из двух шаров, до их удара равен , могут быть направлены как навстречу друг другу, так и в одну сторону. Полный импульс этой системы, состоящей из двух шаров, до их удара равен 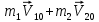 , и он направлен также вдоль линии, соединяющей центры шаров. , и он направлен также вдоль линии, соединяющей центры шаров.
Рассмотрим процессы, происходящие во время удара. При ударе оба шара деформируются, и кинетическая энергия их поступательного движения переходит в потенциальную энергию деформации. При этом между шарами начинают действовать силы отталкивания, равные по величине и противоположные по направлению. В случае центрального удара скорости 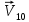 и и 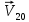 , направлены обе вдоль линии центров. Следовательно, вдоль линий центров направлен и вектор относительной скорости движения шаров, т.е. , направлены обе вдоль линии центров. Следовательно, вдоль линий центров направлен и вектор относительной скорости движения шаров, т.е. 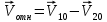 . Деформация обоих шаров происходит симметричным образом относительно линии центров, и силы отталкивания тоже направлены обе вдоль этой линии в противоположные стороны. Под действием этих сил шары отходят друг от друга, деформация уменьшается, и шары постепенно восстанавливают свою форму. Потенциальная энергия их деформации переходит снова в кинетическую энергию, и шары в конце концов разлетаются. Поскольку при ударе силы упругости действуют вдоль линии центров, то шары приобретут какие-то скорости . Деформация обоих шаров происходит симметричным образом относительно линии центров, и силы отталкивания тоже направлены обе вдоль этой линии в противоположные стороны. Под действием этих сил шары отходят друг от друга, деформация уменьшается, и шары постепенно восстанавливают свою форму. Потенциальная энергия их деформации переходит снова в кинетическую энергию, и шары в конце концов разлетаются. Поскольку при ударе силы упругости действуют вдоль линии центров, то шары приобретут какие-то скорости 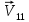 и и 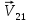 , направленные вдоль линии центров. Таким образом, при центральном ударе шаров эти тела всегда движутся вдоль одной и той же прямой - линии их центров, поэтому этот удар и называют центральным. , направленные вдоль линии центров. Таким образом, при центральном ударе шаров эти тела всегда движутся вдоль одной и той же прямой - линии их центров, поэтому этот удар и называют центральным.
Если шары изготовлены из вещества с ярко выраженными упругими свойствами, то на последней стадии соударения их деформация исчезает почти полностью, и они почти целиком восстанавливают свою первоначальную форму. При этом потенциальная энергия деформации почти полностью превращается снова в кинетическую энергию движения. В идеале можно говорить об абсолютно упругом ударе, когда такое превращение энергии осуществляется полностью. При таком ударе суммарная кинетическая энергия шаров до удара равна их кинетической энергии после удара.
В реальной жизни, конечно, форма соударяющихся шаров после удара восстанавливается не полностью, часть энергии деформации переходит во внутреннюю энергию шаров и, в конечном итоге, рассеивается в виде тепла. В кинетическую же энергию разлетающихся шаров перейдет остальная часть энергии деформации. Таким образом, реальный удар шаров является неупругим. Степень неупругости удара может быть самой различной. Если форма шаров почти полностью восстанавливается и рассеяние энергии в виде тепла мало, то удар близок к абсолютно упругому. Если же деформация шаров на конечной стадии удара остается большой и рассеяние энергии в виде тепла велико, то удар сильно неупругий. Вводят и понятие абсолютно неупругого удара, когда остаточная деформация настолько значительна, что после соударения шары вообще не разлетаются и движутся дальше вместе.
Следует отметить, что время, в течение которого происходит удар, зависит от степени упругости удара. Оно минимально для абсолютно упругого удара.
В любом случае выполняется закон сохранения импульса, т.е.
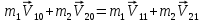 (1) (1)
Абсолютно упругий удар.
Рассмотрим центральный абсолютно упругий удар шаров. При центральном ударе векторы скоростей обоих шаров до и после удара направлены вдоль одной и той же линии - линии центров. Поэтому можно направить вдоль этой линии ось координат; если скорость какого-либо шара направлена вдоль этой оси, то она положительна, если против, то отрицательна. Тогда закон сохранения импульса (1) можно записать в проекции на эту ось, опустив знаки векторов, т.е.:
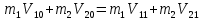 (2) (2)
где скорости берутся со своими знаками.
Как уже говорилось, при абсолютно упругом ударе кинетическая энергия шаров переходит в потенциальную энергию упругой деформации, а та, в свою очередь, полностью переходит в кинетическую энергию разлетающихся шаров: т.е. кинетическая энергия шаров до удара равна кинетической энергии шаров после удара:
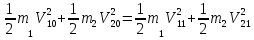 (3) (3)
Уравнения (2) и (3) образуют систему двух уравнений с двумя неизвестными 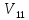 и и 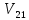 - скоростями шаров после удара. - скоростями шаров после удара.
Решение системы имеет вид:
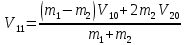 , , 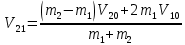 (4) (4)
Коэффициенты восстановления.
Степень упругости удара можно определить с помощью так называемых коэффициентов восстановления скорости K и энергии K1.
Для центрального удара коэффициент восстановления скорости K можно ввести как отношение величины относительной скорости шаров после удара к величине их относительной скорости до удара, т.е.
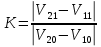 (5) (5)
При абсолютно упругом ударе потенциальная энергия деформации целиком переходит снова в кинетическую энергию и шары разлетаются с максимально возможной относительной скоростью. Относительные скорости шаров до и после абсолютно упругого удара равны по величине и противоположны по направлению. Таким образом для абсолютно упругого удара K=1. Для реального частичного неупругого удара коэффициент K может принимать любые значения от нуля (абсолютно неупругий удар) до единицы, т.е. является мерой степени упругости удара.
Можно ввести также коэффициент восстановления энергии K1, равный отношению суммарной кинетической энергии шаров после и до удара, т.е.
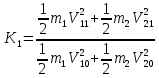 (6) (6)
Максимальное значение коэффициента K1, равное единице, достигается при абсолютно упругом ударе.
Методика эксперимента
Лабораторная установка для изучения упругого удара (рис.1) представляет собой два стальных шара 1 и 2 с массами m1 и m2, закрепленных на бифилярных подвесах 3. Расстояние от оси вращения шаров до их центров масс равно L. Шар m1 может удерживаться в отклоненном положении электромагнитом 4. Положение электромагнита может изменяться за счет поворота штанги 5. Начальный угол отклонения подвеса шара m1 от вертикального положения определяется с помощью поворотного индикатора 6 и шкалы 7. Этот же индикатор позволяет определить максимальный угол отклонения шара m1 после удара. Максимальный угол отклонения шара m2 измеряется с помощью второго поворотного индикатора 8 со шкалой 9. Устройство 10 позволяет предотвратить отклонение шара m2 после соударения с шаром m1, если это необходимо. Для этого его устанавливают в вертикальное положение. Управление электромагнитом осуществляется с помощью блока 11.
Величинами, которые будут измеряться в опытах, являются не скорости, а углы отклонения подвесов шаров от положения равновесия. Поэтому формулы для скоростей, получим через выражения для углов отклонения каждого из шаров после первого удара.
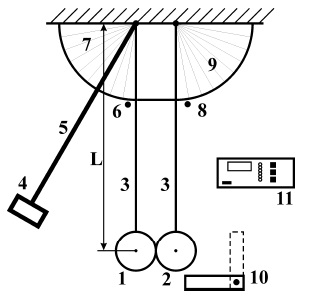
рис. 1
Пусть удерживаемый электромагнитом шар m1 имеет подвес, расположенный под углом α10 к вертикальному направлению. Если расстояние от оси вращения до центра масс шара равно L, то в таком положении центр масс поднят на высоту h10 , которая равна
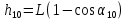 . (7) . (7)
Считаем, что в положении равновесия центр масс шара расположен на нулевой высоте.
Из закона сохранения механической энергии следует
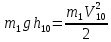 (8) (8)
Следовательно,
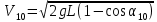 . (9) . (9)
Подставляя (9) в формулу (4) и учитывая что второй шар покоится до удара, получаем теоретическую скорость первого шара после удара выраженную через угол
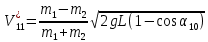 . (10) . (10)
Угол отклонения подвеса первого шара после удара обозначим α11. Связь этого угла с высотой подъема после удара h11 имеет вид:
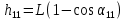 . (11) . (11)
Опять пользуемся законом сохранения механической энергии
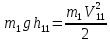 (12) (12)
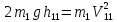 (13) (13)
Выразим из (13) реальную скорость первого шара после удара с учетом (11)
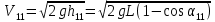 (14) (14)
Рассуждая таким же образом, получим рабочую формулу для скорости второго шара после первого удара угла через косинус угла отклонения α21:
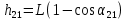 ; (15) ; (15)
Из (4) с учетом (9) получаем теоретическую скорость второго шара после удара
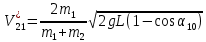 . (16) . (16)
Из закона сохранения механической энергии для второго шара найдем его реальную скорость после удара
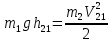 (17) (17)
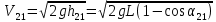 (18) (18)
Коэффициент восстановления скорости K с учетом (9), (14) и (18) запишется соответственно
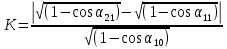 (19) (19)
Коэффициент восстановления энергии примет вид
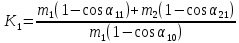 (20) (20)
Порядок выполнения работы
Убедитесь, что в качестве шара m1 вначале используется шар меньшей массы. Если это не так, закрепите его. Шар m2 должен иметь большую массу. Заготовьте таблицу.
Таблица
№
|
|
α10
|
α11
|
α21
|
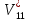 , м/с , м/с
|
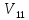 , м/с , м/с
|
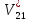 , м/с , м/с
|
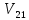 , м/с , м/с
|
K
|
K1
|
1
|
m1<m2
|
15
|
|
|
|
|
|
|
|
|
2
|
30
|
|
|
|
|
|
|
|
|
3
|
45
|
|
|
|
|
|
|
|
|
1
|
m1=m2
|
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
|
|
Включите электронный блок управления электромагнитом.
Подведите к электромагниту шар m1. Убедитесь, что он удерживается электромагнитом. Установите поворотом штанги 5 начальный угол α10 отклонения подвеса шара m1 от вертикали. Пользуясь поворотным индикатором 6 и шкалой 7 (см. Рис.1), измерьте этот угол.
Подготовьте поворотный индикатор 8 к измерению отклонения шара m2. Для этого установите его в положение близкое к 00.
Нажатием кнопки на электронном блоке отключите питание электромагнита и освободите шар m1.
Снимите показания со шкалы 9 и запишите полученное значение угла α21.
Нажатием кнопки «Стоп» включите питание электромагнита и вновь подведите к нему шар m1.
Подготовьте поворотный индикатор 6 для определения угла отклонения шара m1 после первого удара. Для этого установите его в положение близкое к 00. Установите устройство 10 в вертикальное положение. Это не позволит шару m2 после повторного удара изменить показания поворотного индикатора 6.
Нажатием кнопки на электронном блоке отключите питание электромагнита и освободите шар m1. После удара шар m2 должен «прилипнуть» к держателю 10, тем самым не произведется повторный удар.
Снимите показание со шкалы 7 и запишите полученное значение угла α11. Показания углов α10, α11, α21 запишите в таблицу.
Рассчитайте экспериментальные и теоретические значения скоростей шаров по соответствующим формулам (10) и (14), (16) и (18). Сравните результаты.
Повторите п. 2 - 10 для других значений начального угла α10 , изменив его поворотом штанги 5. Проведите вычисления и запишите их в таблицу.
Снимите шар малой массы и замените его шаром, масса которого равна массе шара m2.
Уберите устройство 10, препятствующее отклонению второго шара.
Проведите опыты с шарами равной массы при трех различных начальных углах α10. Убедитесь, что, действительно, при ударе они обмениваются импульсами и энергиями.
Вычислите скорости обоих шаров после удара. Результаты измерений и вычислений занесите в таблицу.
Для всех проведенных опытов рассчитайте коэффициенты восстановления скорости и энергии по формулам (19) и (20).
Проверьте, выполняется ли закон сохранения импульса и механической энергии при ударах шаров. Сделайте соответствующие выводы.
Контрольные вопросы
Какой удар называется абсолютно упругим?
Опишите процесс столкновения шаров. Какие энергетические превращения при этом происходят?
Как определить скорости шаров после абсолютно упругого удара, если до удара шары двигались навстречу друг другу с разными скоростями?
Получите формулы (4) решив систему уравнений (2) и (3). Проанализируйте частные случаи.
Что показывает коэффициент восстановления скорости?
Что показывает коэффициент восстановления энергии?
Чему равны коэффициенты восстановления скорости и энергии при абсолютно упругом ударе? При абсолютно неупругом ударе?
Является ли удар шаров в данной работе абсолютно упругим? Из чего это следует?
|
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.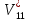 , м/с
, м/с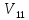 , м/с
, м/с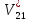 , м/с
, м/с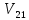 , м/с
, м/с
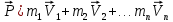
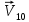 и
и 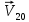 , а затем сталкиваются. После соударения изменится направление их движения и величина их скорости.
, а затем сталкиваются. После соударения изменится направление их движения и величина их скорости. 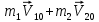 , и он направлен также вдоль линии, соединяющей центры шаров.
, и он направлен также вдоль линии, соединяющей центры шаров. 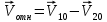 . Деформация обоих шаров происходит симметричным образом относительно линии центров, и силы отталкивания тоже направлены обе вдоль этой линии в противоположные стороны. Под действием этих сил шары отходят друг от друга, деформация уменьшается, и шары постепенно восстанавливают свою форму. Потенциальная энергия их деформации переходит снова в кинетическую энергию, и шары в конце концов разлетаются. Поскольку при ударе силы
. Деформация обоих шаров происходит симметричным образом относительно линии центров, и силы отталкивания тоже направлены обе вдоль этой линии в противоположные стороны. Под действием этих сил шары отходят друг от друга, деформация уменьшается, и шары постепенно восстанавливают свою форму. Потенциальная энергия их деформации переходит снова в кинетическую энергию, и шары в конце концов разлетаются. Поскольку при ударе силы 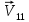 и
и 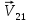 , направленные вдоль линии центров. Таким образом, при центральном ударе шаров эти тела всегда движутся вдоль одной и той же прямой - линии их центров, поэтому этот удар и называют центральным.
, направленные вдоль линии центров. Таким образом, при центральном ударе шаров эти тела всегда движутся вдоль одной и той же прямой - линии их центров, поэтому этот удар и называют центральным.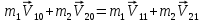 (1)
(1)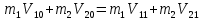 (2)
(2)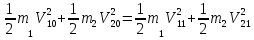 (3)
(3)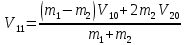 ,
, 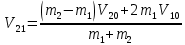 (4)
(4)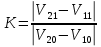 (5)
(5)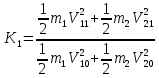 (6)
(6)
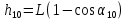 . (7)
. (7)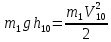 (8)
(8)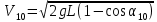 . (9)
. (9)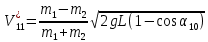 . (10)
. (10)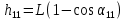 . (11)
. (11)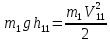 (12)
(12)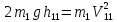 (13)
(13)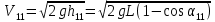 (14)
(14)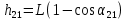 ; (15)
; (15)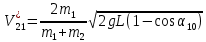 . (16)
. (16)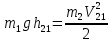 (17)
(17)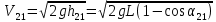 (18)
(18)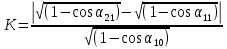 (19)
(19)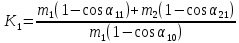 (20)
(20)