|
|
механика_лабораторные работы. Контрольные вопросы для самопроверки. Пособие содержит методические указания по теории погрешностей. Работы расположены в последовательности изложения материала курса Общая физика, раздел Механика
Лабораторная работа №6
ИЗМЕРЕНИЕ СКОРОСТИ ПУЛИ С ПОМОЩЬЮ
БАЛЛИСТИЧЕСКОГО МАЯТНИКА
Цель работы: Ознакомится с одним из примеров применения законов сохранения импульса и механической энергии при решении баллистических задач. С помощью баллистического маятника определить скорости пуль с различными массами.
Приборы и принадлежности: Модульный учебный комплекс МУК-М1: рабочий узел «баллистический маятник», набор пуль с разными массами.
Краткое теоретическое введение
Баллистический маятник представляет собой массивный цилиндр массой М, который подвешен на невесомых и нерастяжимых нитях так, что он может двигаться только поступательно. В цилиндр в горизонтальном направлении производят выстрел пулей массы т из пружинного пистолета, неподвижно закрепленного вблизи маятника (рис.1). Если торцевая стенка цилиндра изготовлена из мягкого и легко деформируемого материала, например, пластилина, то пуля при попадании может испытывать абсолютно неупругий удар. Абсолютно неупругий удар – это удар, при котором потенциальная энергия упругой деформации не возникает; кинетическая энергия тел частично либо полностью превращается во внутреннюю энергию; после удара тела двигаются с одинаковой скоростью (т.е. как единое тело) либо покоятся. При таком ударе выполняется только закон сохранения импульса, закон же сохранения механической энергии не соблюдается - механическая энергия частично или полностью переходит во внутреннюю.
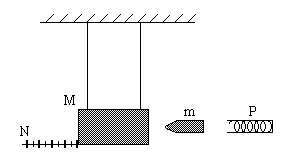
рис.1
Если зарядить пистолет пулей, то в сжатой при этом пружине будет запасена потенциальная энергия:
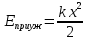 (1) (1)
где k – коэффициент упругости, x – деформация пружины.
Предположим, что вся энергия сжатой пружины при выстреле полностью превращается в кинетическую энергию пули. Это означает, что мы пренебрегаем потерями энергии на преодоление трения между пулей и стволом пистолета и на сообщение кинетической энергии самой пружине. Учтем, кроме того, что геометрические размеры всех пуль одинаковы, а, значит, одинакова деформация для любой пули, и, следовательно, одинакова запасаемая пружиной потенциальная энергия. Тогда из закона сохранения механической энергии следует, что пули различных масс, вылетая из пружинного пистолета, должны иметь одинаковые кинетические энергии:
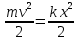 (2) (2)
где v – скорость пули после выстрела.
Из (2) получаем зависимость скорости пули после выстрела от ее массы:
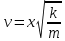 (3) (3)
Поскольку величины xи kдля всех пуль одинаковы, то график ожидаемой зависимости скорости пули 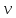 от от 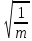 , должен, согласно формуле (3), представлять собой прямую линию, проходящую через начало координат. , должен, согласно формуле (3), представлять собой прямую линию, проходящую через начало координат.
Пролетев небольшое расстояние между пистолетом и маятником, пуля входит в пластилин, заполняющий цилиндр, и за счет вязкого трения быстро теряет скорость. При этом часть механической энергии пули расходуется на неупругую деформацию и превращается во внутреннюю энергию пластилина и пули, то есть пластилин и пуля нагреваются.
Процесс удара является кратковременным. Если масса маятника велика по сравнению с массой пули (M>>m), то за время удара он в силу своей инерционности не успевает выйти из положения равновесия. Это позволяет считать систему маятник-пуля в момент удара замкнутой в горизонтальном направлении, так как сила тяжести и сила натяжения подвеса направлены вертикально при вертикальном положении маятника. Для замкнутой системы можно применить закон сохранения импульса:
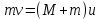 , (4) , (4)
где 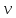 - скорость пули до удара (при этом скорость маятника равна нулю), u - скорость, приобретенная системой маятник-пуля сразу после удара. - скорость пули до удара (при этом скорость маятника равна нулю), u - скорость, приобретенная системой маятник-пуля сразу после удара.
Маятник вместе с пулей, получив за счет неупругого удара импульс, отклоняется от положения равновесия на угол α.В процессе отклонения на маятник действует сила тяжести (вниз) и сила упругости подвеса (перпендикулярно направлению мгновенной скорости маятника). Если пренебречь потерями энергии на трение в подвесе и на сопротивление воздуха, то работу при отклонении маятника совершает только гравитационная сила. Это позволяет воспользоваться законом сохранения механической энергии:
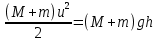 (5) (5)
где h – наибольшая высота, на которую поднимается маятник (рис.2).
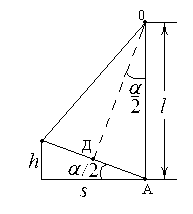
рис. 2
Слева в этой формуле кинетическая энергия при поступательном движении маятника сразу после удара (в этой точке потенциальную энергию принимаем равной нулю), а справа – потенциальная энергия системы в момент ее остановки на высоте h.
Решая совместно (4) и (5) получим
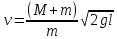 (6) (6)
Таким образом, найдя значение высоты подъема маятника можно рассчитать скорость полета пули.
Методика эксперимента
Практическое измерение высоты подъема маятника затруднительно. Поэтому в лабораторном комплексе МУК–М1 предусмотрено измерение горизонтального смещения маятника s.
Выразим высоту h через соответствующее горизонтальное смещение маятника s, которое удобнее измерять. Предположим, что угол отклонения маятника от положения равновесия α мал. Из рис.2 видно, что
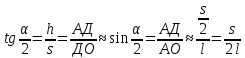 (7) (7)
где l – длина нити подвеса.
Из (7) получаем
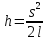 (8) (8)
Подставляя (8) в (6) получим выражения для вычисления скорости пули 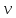 перед ударом перед ударом
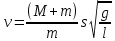 (9) (9)
Выражение (9) позволяет, осуществив прямые измерения смещения маятника s и зная значения остальных величин, входящих в эту рабочую формулу, определить скорость пули 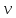 путем косвенных измерений. Измерив скорости для пуль с разными массами можно, следовательно, убедиться в справедливости теоретической зависимости (3). путем косвенных измерений. Измерив скорости для пуль с разными массами можно, следовательно, убедиться в справедливости теоретической зависимости (3).
Порядок выполнения работы
Зарядите пружинный пистолет пулей (рекомендуется начать с пули с наибольшей массы).
Подготовьте устройство N (см. рис.1) к измерению горизонтального смещения маятника. Измерьте численное значение начальной координаты sнач маятника по линейки отсчетного устройства N. Запишите в таблицу.
Осуществите первый выстрел, нажав пусковой рычаг пружинного пистолета. Запишите численное значение конечной координаты sкон, определив его по линейке отсчетного устройства N. Вычислите смещение маятника при первом опыте
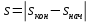 . .
По формуле (9) получите оценку значения скорости пули 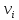 . .
Проведите с данной пулей не менее трех выстрелов. Вычислите скорость 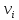 для каждого выстрела. для каждого выстрела.
Вычислите среднее значение скорости данной пули.
Все измерения и вычисления зафиксируйте в таблице.
Таблица
№
|
mпули, кг
|
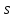 нач, м нач, м
|
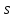 кон, м кон, м
|
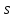 , м , м
|
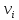 , м/с , м/с
|
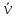 , м/c , м/c
|
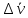
|
δ, %
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
|
Проведите эксперименты с пулями других масс и вычислите их скорости (повторяя пункты с 1 по 7). Учитывая, что для приведенных опытов должна выполняться зависимость (3), постройте графики этой зависимости в координатах v, 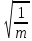 для используемых в опытах пуль разных масс и полученных для них скоростей. Сравните ход полученного графика с теоретическим. для используемых в опытах пуль разных масс и полученных для них скоростей. Сравните ход полученного графика с теоретическим.
Выведите формулы для абсолютной и относительной погрешности косвенного измерения скорости пули, считая массы пули и маятника, а также длину нити константами.
Вычислите погрешности. Результаты занесите в таблицу.
Сделайте выводы.
Контрольные вопросы
Что такое баллистический маятник?
Какой удар называется абсолютно упругим?
Какой удар называется неупругим?
Сформулируйте закон сохранения импульса.
Сформулируйте закон сохранения механической энергии.
Какие законы сохранения выполняются при неупругом столкновении пули с маятником?
Опишите все энергетические превращения, происходящие в эксперименте.
Выведите формулу (9).
*Выведите формулу, по которой можно рассчитать энергию Q перешедшую во внутреннюю энергию маятника при неупругом столкновении пули с маятником.
Какие в данной работе возникают погрешности измерений?
Какими силами пренебрегли в работе? Что изменится если их учесть?
|
|
|
 Скачать 0.7 Mb.
Скачать 0.7 Mb.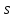 нач, м
нач, м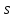 кон, м
кон, м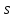 , м
, м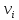 , м/с
, м/с 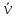 , м/c
, м/c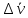
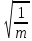 для используемых в опытах пуль разных масс и полученных для них скоростей. Сравните ход полученного графика с теоретическим.
для используемых в опытах пуль разных масс и полученных для них скоростей. Сравните ход полученного графика с теоретическим.

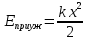 (1)
(1)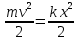 (2)
(2)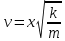 (3)
(3)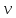 от
от 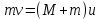 , (4)
, (4)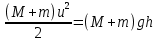 (5)
(5)
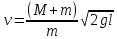 (6)
(6)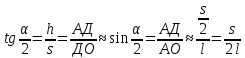 (7)
(7)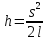 (8)
(8)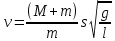 (9)
(9)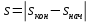 .
.